采样定理

连续时间信号也叫模拟信号。在一定条件之下，模拟信号可以用该信号在等时间间隔点上的值或样本来表示，且利用这些样本值能将该信号全部恢复出来。采样定理就是讨论采样出来的数据如何恢复出原信号的一些条件。

一、采样定理结论

二、奈奎斯特间隔和频率计算公式及例题：

• 公式：
  
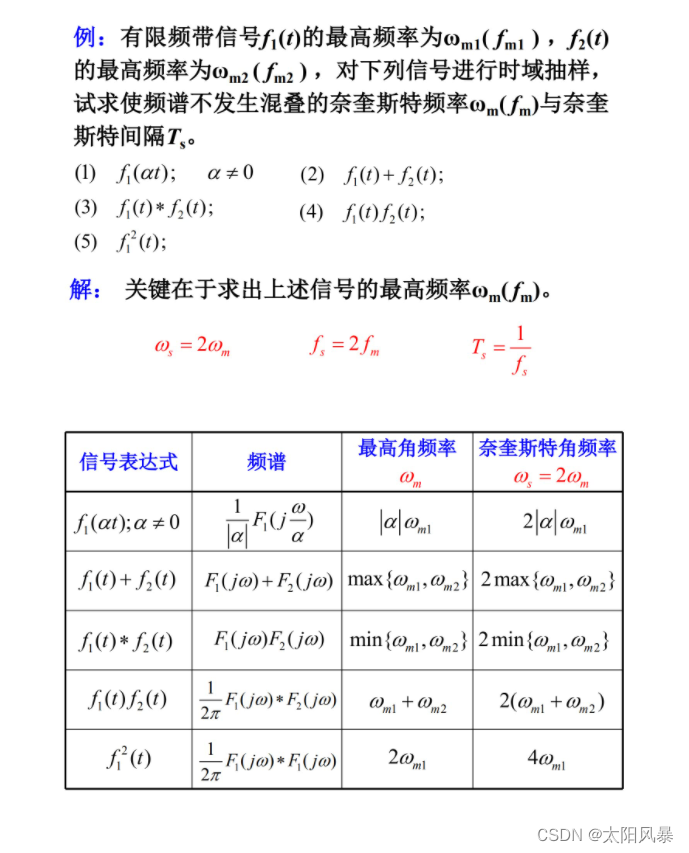
• 例题：
  

下面是具体的一些原理，很简单的。

三、信号自然采样（脉冲采样）

图 4.8-1 是对信号 f (t)采样过程的等效示意图。模拟（连续）信号 f (t)，通过一个开关电路，即抽样器，开关以一定的频率闭合、打开，这样输出信号 f_s(t) 就是 f (t) 经过采样后的信号，这个采样过程叫 自然采样，也称为脉冲采样。

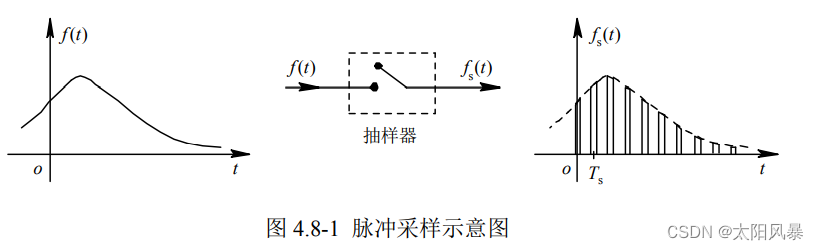
数学建模一下其实就是推断出这样的。
采样过程可以用信号 f (t)和一个开关函数 p(t) 的乘积来描述

• f_s(t) = f(t)p(t); p(t) 为周期脉冲串
  
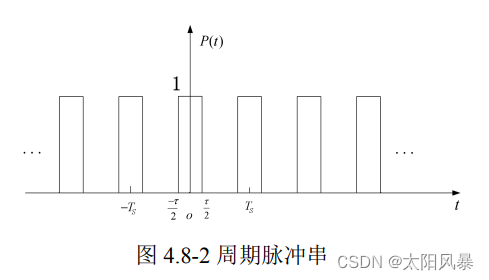
  假定 f (t)为频谱受限信号，其傅里叶变换为 F(jω) ，即 f (t) <–> F(jω)，采样脉冲序列的傅里叶变换为 P(jω) ，即 p(t)  <–> P(jω) ，设采样周期为 T_s，则采样角频率为
  
  由于 p(t) 是矩形周期信号，其傅里叶变换：
  
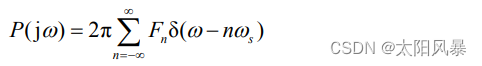
  其中
  
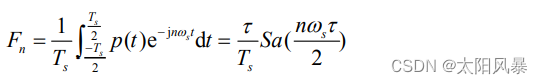
  用频域卷积性质
  
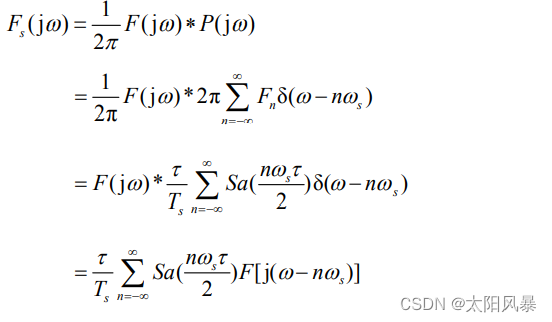
  由此可见，当采样脉冲为矩形抽样脉冲时，幅度以 Sa 函数的规律变化。 采样后的信号频谱包括有原信号的频谱以及无限个经过平移的原信号的频谱，平移的频率为采样频率及其各次谐波频率。且平移后的频谱幅值随频率而呈 Sa 函数分布。采样前后信号的频谱如图 4.8-3 所示，图中ω_m 为信号的最高频率。
  
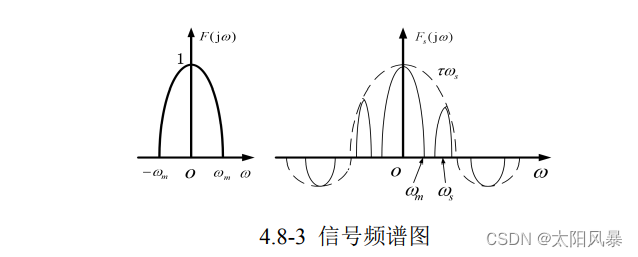
  可见，要从采样后的信号恢复到采样前的信号，可以用低通滤波器将中间的一段频谱滤出来，但是，如果采样角频率 ω_s 太小，采样后将会出现如图 4.8-4 所示，这种现象叫频谱混叠，其实就是其他谐波和中间的0次谐波有重叠
  
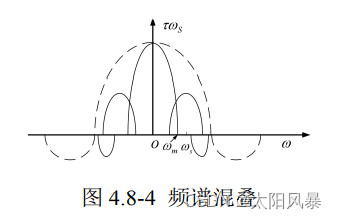
  出现混叠现象是无法恢复出采样之前的信号。要想恢复出采样之前的信号，要满足以下条件
  ω_s - ω_m ≥ ω_m 或
  
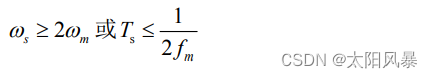
  为了保留这一频率分量的全部信息，一个周期的间隔内至少抽样两次，即必须满足
  

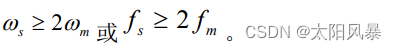
四、信号理想采样（冲激采样）

在理想情况下，采样可以等效下图

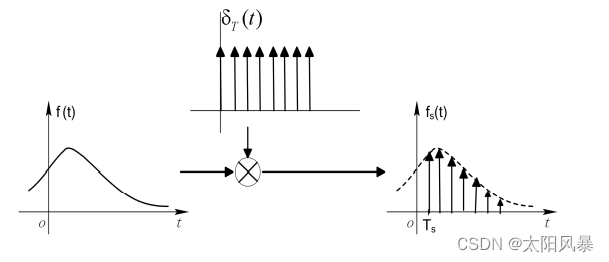
当然这个是可以实现的，用欧拉公式把 cos 函数 或者 sin函数 就变成 指数形式
采样后信号：

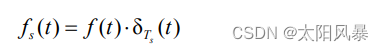
其中

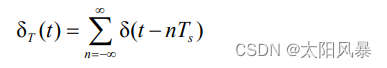
δ_T(t) 的傅里叶系数为 ：

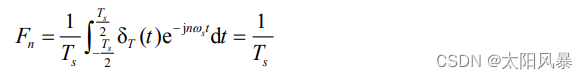
冲激采样信号的频谱也为周期性冲激形式：

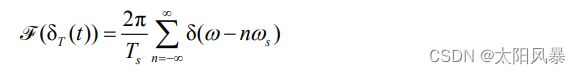
采样后信号的时域表达式为：

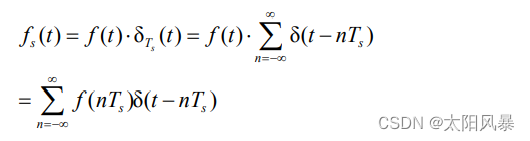
采样后信号的傅里叶变换为：

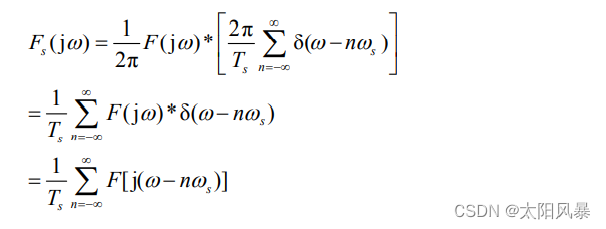
采样前后信号的频谱如下图

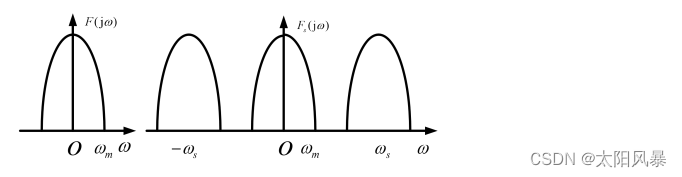
由此可知，采样后信号的频谱是采样前信号频谱的平移和叠加，只要采样频率足够大，就可用低通滤波器，从采样后的信号中恢复出采样前信号。同时要使采样后频谱不混叠 只有满足 ω_s ≥ 2ω_m 或 f_s ≥ 2f_m 条件，F_s (jω) 才不会产生频率的混叠。这样，抽样信号 f_s(t) 保留了原连续信号 f(t) 的全部信息，完全可以用 f_s(t) 唯一地表示 f (t)，或者说，完全可以由f_s(t) 恢复出 f(t) 。

• 由此可以得出采样定理：