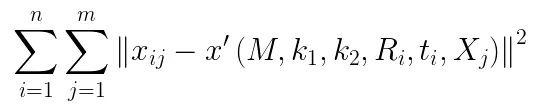翻译:
您得到一个有根的树,其中包含从1到𝑛编号为𝑛的顶点。根结点是顶点1。还有一个字符串𝑠表示每个顶点的颜色:如果𝑠𝑖=𝙱,那么顶点𝑖是黑色的,如果𝑠𝑖=𝚆,那么顶点𝑖是白色的。
如果白色顶点的数量等于黑色顶点的数量,则该树的子树称为平衡的。计算平衡子树的数量。
树是没有循环的连通无向图。有根树是一棵有选定顶点的树,称为根。在这个问题中,所有树的根都是1。
该树由包含𝑛−1数字的父数组𝑎2,…,𝑎𝑛指定:对于所有𝑖=2,…,𝑛,𝑎𝑖是顶点的父数组,其数字为𝑖。顶点𝑢的父顶点是从𝑢到根节点的简单路径上的下一个顶点。
顶点𝑢的子树是所有通过𝑢到达根的简单路径的顶点集合。例如,在下图中,7在3的子树中,因为简单路径7→5→3→1经过3。注意,顶点包含在它的子树中,而根的子树就是整个树。
这张照片显示的树𝑛= 7,𝑎=[1,1,2,3,3,5],和𝑠=𝚆𝙱𝙱𝚆𝚆𝙱𝚆。顶点3处的子树是平衡的。
输入
第一行输入包含一个整数𝑡(1≤𝑡≤104)——测试用例的数量。
每个测试用例的第一行包含一个整数𝑛(2≤𝑛≤4000)——树中的顶点数量。
每个测试用例的第二行包含𝑛−1整数𝑎2,…,𝑎𝑛(1≤𝑎𝑖<𝑖)-顶点2,…,𝑛的父结点。
每个测试用例的第三行包含一个长度为𝑛的字符串𝑠,由字符𝙱和𝚆组成——这是树的颜色。
保证所有测试用例的𝑛值的总和不超过2⋅105。
输出
对于每个测试用例,输出一个整数——平衡子树的数量。
例子
inputCopy
3.
7
1 1 2 3 3 5
WBBWWBW
2
1
BW
8
1 2 3 4 5 6 7
BWBWBWBW
outputCopy
2
1
4
请注意
第一个测试用例如图所示。只有顶点2和3处的子树是平衡的。
在第二个测试用例中,只有顶点1的子树是平衡的。
在第三个测试用例中,只有顶点1、3、5和7处的子树是平衡的。
思路:
典型的树形dp板子,我们给每个节点赋值,然后父其节点转移。
代码:
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long ll;
int n,t;
inline __int128 read(){
__int128 x = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){
if(ch == '-')
f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9'){
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
inline void print(__int128 x){
if(x < 0){
putchar('-');
x = -x;
}
if(x > 9)
print(x / 10);
putchar(x % 10 + '0');
}
vector<int>q[4005];
string s;
int an=0,bn=0,cn=0;
ll dp[4005];
void dfs(int x,int fa){
for (int i =0; i<q[x].size(); i++) {
dfs(q[x][i],x);
}
if (s[x]=='W') {
dp[x]+=1;
}
else{
dp[x]+=-1;
}
dp[fa]+=dp[x];
}
int we;
void solv(){
memset(dp, 0, sizeof dp);
cin>>n;
for (int i =0; i<=n; i++) {
q[i].clear();
}
for (int i =2; i<=n; i++) {
cin>>we;
q[we].push_back(i);
}
cin>>s;
s=' '+s;
dfs(1,0);
int na=0;
// for (int i=1; i<=n; i++) {
// printf("%lld ",dp[i]);
// }
// printf("\n");
for (int i =1; i<=n; i++) {
if (dp[i]==0) {
na++;
}
}
printf("%d\n",na);
}
int main(){
ios::sync_with_stdio(false);
cin.tie(); cout.tie();
cin>>t;
while (t--) {
solv();
}
return 0;
}