0 简介

论文：A Simple Framework for Contrastive Learning of Visual Representations
代码：https://github.com/google-research/simclr
发表：2020年发表在ICML会议上

1 核心思想

如何构建对比学习的比较对象？本文按如下方式进行构建：

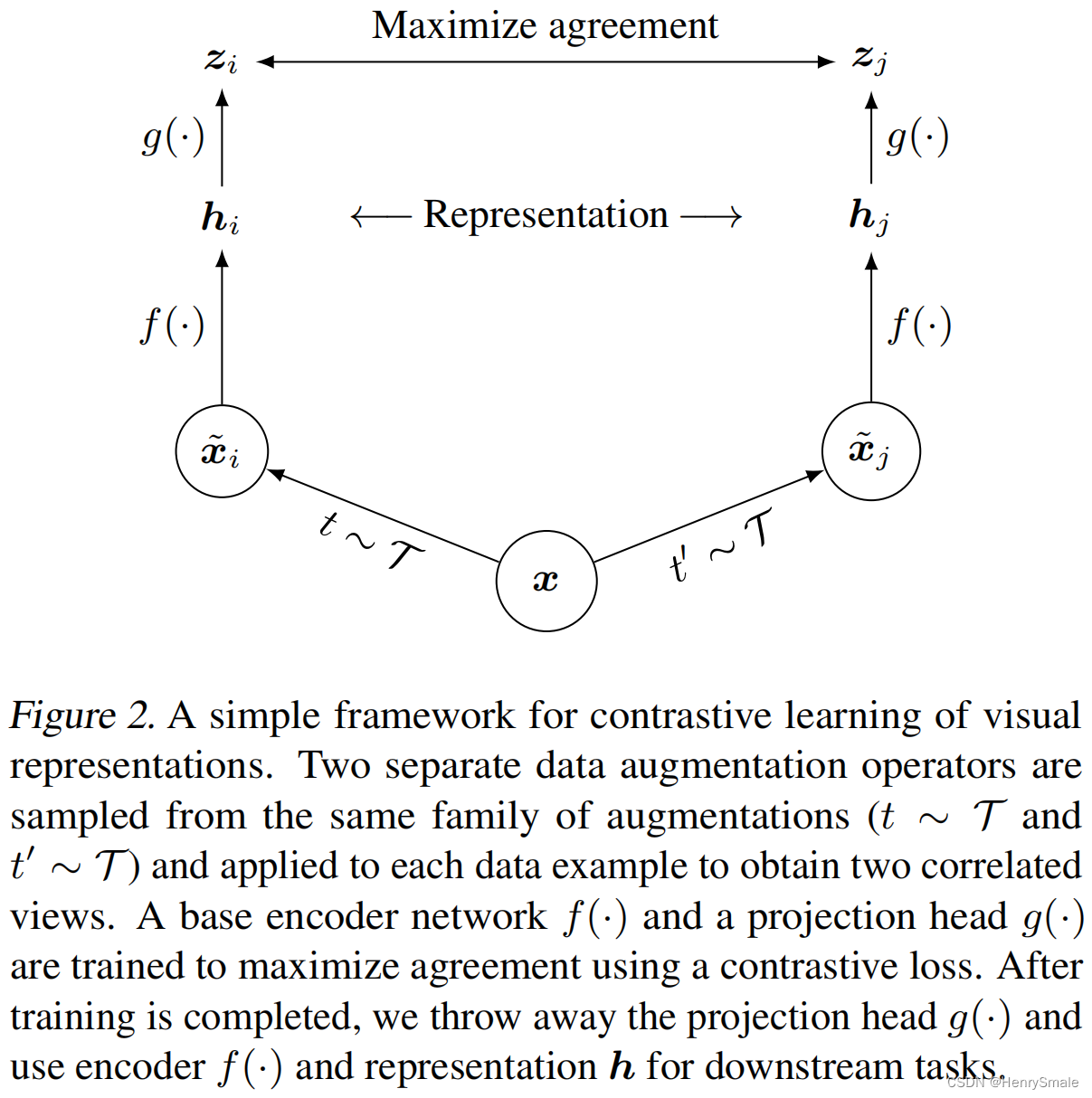
• 数据增强：输入$x$，增强为${\tilde{x}}_i$($t\sim \mathcal{T}$)和${\tilde{x}}_j$($t^{\prime }\sim \mathcal{T}$)，获得两个相关的视角，这两个相关的视角的距离越近越好；
• 和其他图片增强的视角进行对比：$x$的视角和其他图片增强得到的视角距离越远越好。
  

1.1 总体步骤

具体步骤如下：

• 输入图像$x$，对其进行两种不同增强得到两张新图片${\tilde{x}}_i$($t\sim \mathcal{T}$)和${\tilde{x}}_j$($t^{\prime }\sim \mathcal{T}$)；
• 将两张新图片输入ResNet，即$f(\cdot )$提取特征，得到$h_i,h_j$；
• 两个特征向量经过MLP网络，即$g(\cdot )$处理，得到$z_i,z_j$。

假设batch size大小为$N$，经过数据增强，可以得到$2N$张图像。
SimCLR在对比学习时，需要正负例：

• $z_i,z_j$构成正例；
• $z_i$与batch size中其他图像（包括数据增强后的图像）的特征向量组成负例对，因此一张图片将存在1个正例对，$2N-2$个负例对。

一张图片的损失函数为：
$${\ell }_{i,j}=-\log \frac{\exp \left(\mathrm{sim}\left({\mathbf{z}}_i,{\mathbf{z}}_j\right)/\tau \right)}{{\sum }_{k=1}^{2N}{1}_{[k\ne i]}\exp \left(\mathrm{sim}\left({\mathbf{z}}_i,{\mathbf{z}}_k\right)/\tau \right)}$$
其中$\mathrm{sim}\left({\mathbf{z}}_i,{\mathbf{z}}_j\right)$表示余弦相似度， 1 [ k ≠ i ] ∈ { 0 , 1 } \mathbb{1}_{[k \neq i]} \in \{0, 1\} 1[k=i]​∈{0,1},当$k\ne i$等于1，$k==i$等于0，$\tau$为温度系数。
$2N$张图像的损失函数之和求平均，得到最终的损失函数：
$$\mathcal{L}=\frac{1}{2N}\sum _{k=1}^N\left[\ell (2k-1,2k)+\ell (2k,2k-1)\right].$$

1.2 增强图片的方式

• 随机裁剪（random cropping）；
• 随机颜色失真（random color distortions）；
• 随机高斯模糊（random Gaussian blur）。
  
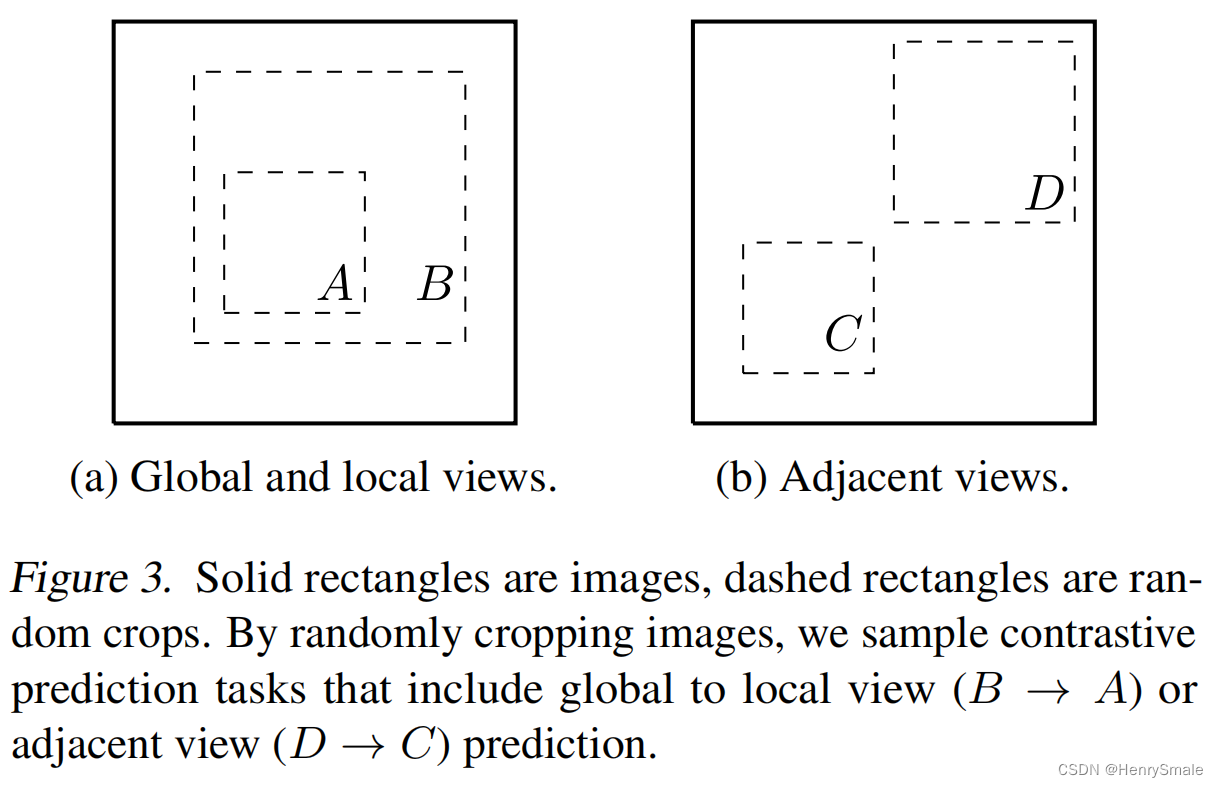
  实矩形是原始图像，虚线矩形是随机裁剪。通过随机裁剪图像，我们采样对比预测任务，包括全局到局部视图($B\to A$)或相邻视图($D\to C$)预测。
  

1.2 特征提取

$${\mathbf{h}}_i=f\left({\tilde{\mathbf{x}}}_i\right)=\mathrm{ResNet}\left({\tilde{\mathbf{x}}}_i\right)$$
其中${\mathbf{h}}_i\in {\mathbb{R}}^d$。
$${\mathbf{z}}_i=g\left({\mathbf{h}}_i\right)=W^{(2)}\sigma \left(W^{(1)}{\mathbf{h}}_i\right)$$
其中$\sigma$就是一个ReLU非线性操作。

2 具体算法

总体分为三个重要的过程：

• 数据增强，通过两个增强函数操作，图片成对存储$[({\tilde{x}}_1,{\tilde{x}}_2),({\tilde{x}}_3,{\tilde{x}}_4),\dots ,({\tilde{x}}_{2k-1},{\tilde{x}}_{2k}),\dots ,({\tilde{x}}_{2N-1},{\tilde{x}}_{2N})$；
• 特征提取，经过ResNet(对应$f(\cdot )$)操作和MLP(对应$g(\cdot )$)操作后，得到特征向量组$[(z_1,z_2),(z_3,z_4),\dots ,(z_{2k-1},z_{2k}),\dots ,(z_{2N-1},z_{2N})$
  
• 对比学习，先是${\tilde{x}}_{2k-1}$和其它图片进行对比学习，然后是${\tilde{x}}_{2k}$和其它图片进行对比学习
  

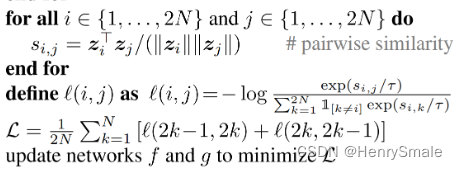
3 实验

本文的实验分析非常有用，讨论了模型在什么情况下更有效，有利于读者选择合适的参数。

3.1 数据增强方式对性能的影响

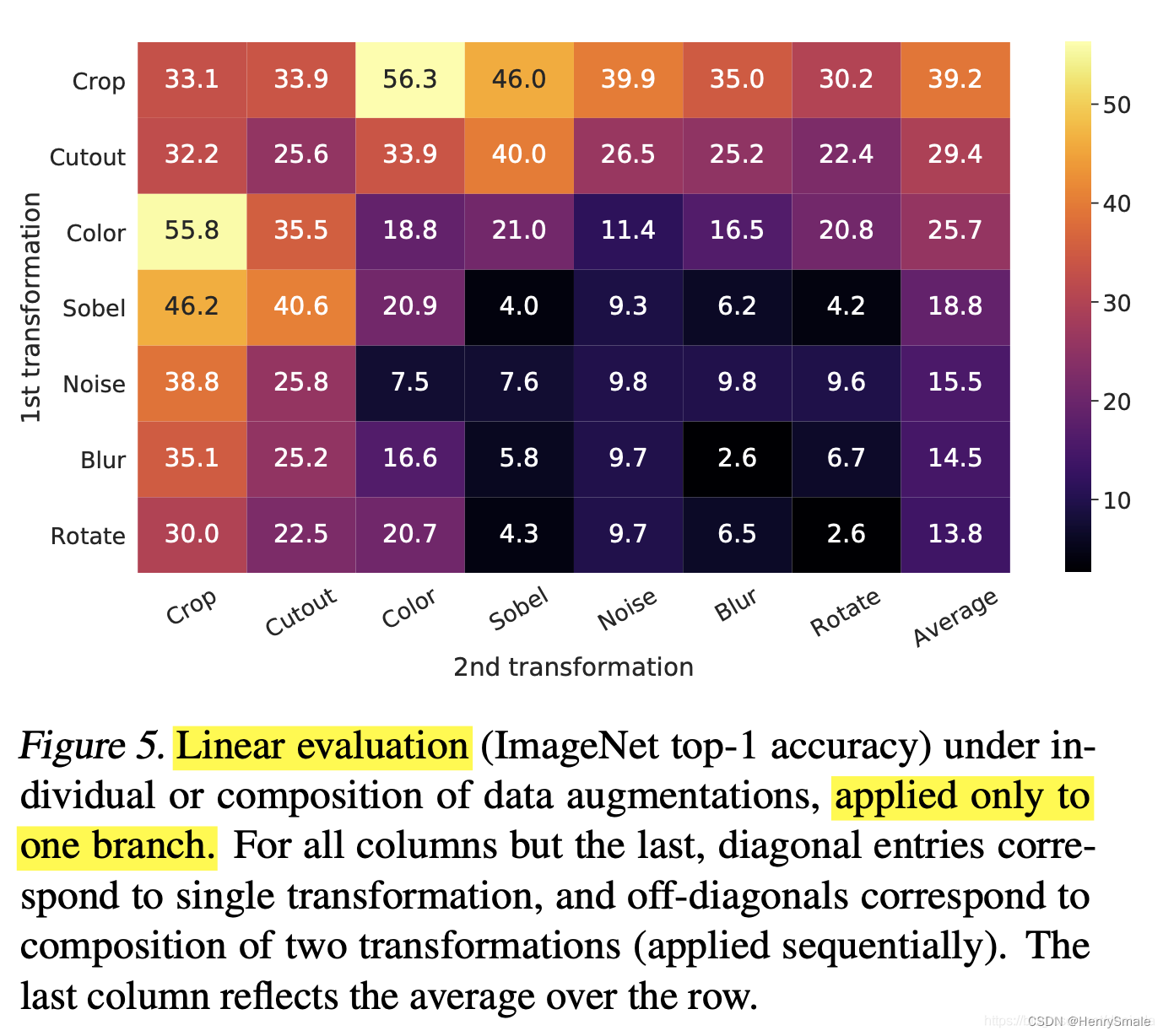
【问】：怎么理解这个图？
【答】：以左上角的33.1为例，第一次数据增强采用Crop方法，第二次数据增强采用Crop方法；以左上角33.9为例，第一次数据增强采用Crop方法，第二次数据增强采用Cutout方法。
得到如下三个结论：

• 单独使用一种数据增强，对比学习的效果会很差；
• 效果最好的组合：第一次数据增强采用Crop方法，第二次数据增强采用Color方法，得到的精度为56.3；效果次好的组合：第一次数据增强采用Color方法，第二次数据增强采用Crop方法，得到的精度为55.8；
• 数据增强方式对对比学习的影响非常明显，这不是一个好的性质，很多时候我们需要进行穷举试错。

3.2 模型宽度和深度对性能的影响

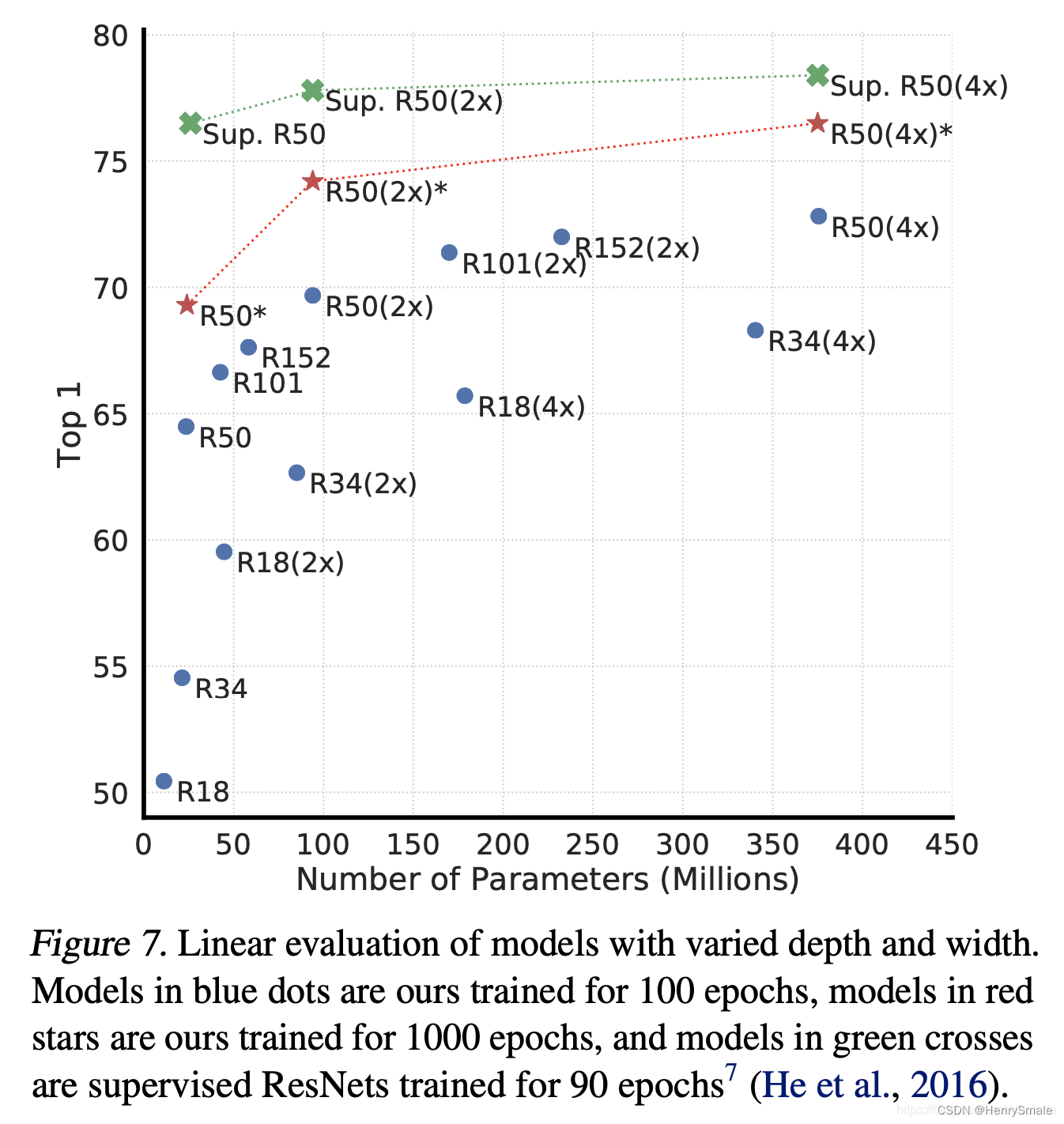
【问】：怎么理解这个图？
【答】：以R18(4x)为例说明，R18表示18层的ResNet网络，4x表示模型宽度加宽4倍。
从图上可以得到如下结论：

• 增大模型容量时，优先增加模型的深度，比如ResNet152比ResNet18性能高不少，参数量并没有增加多少；
• 次选增加模型的宽度，比如ResNet18(4x)比ResNet18(2x)性能高一些，但参数量增加较多，导致训练速度变慢。

3.3 特征向量$z_i$的长度对性能的影响

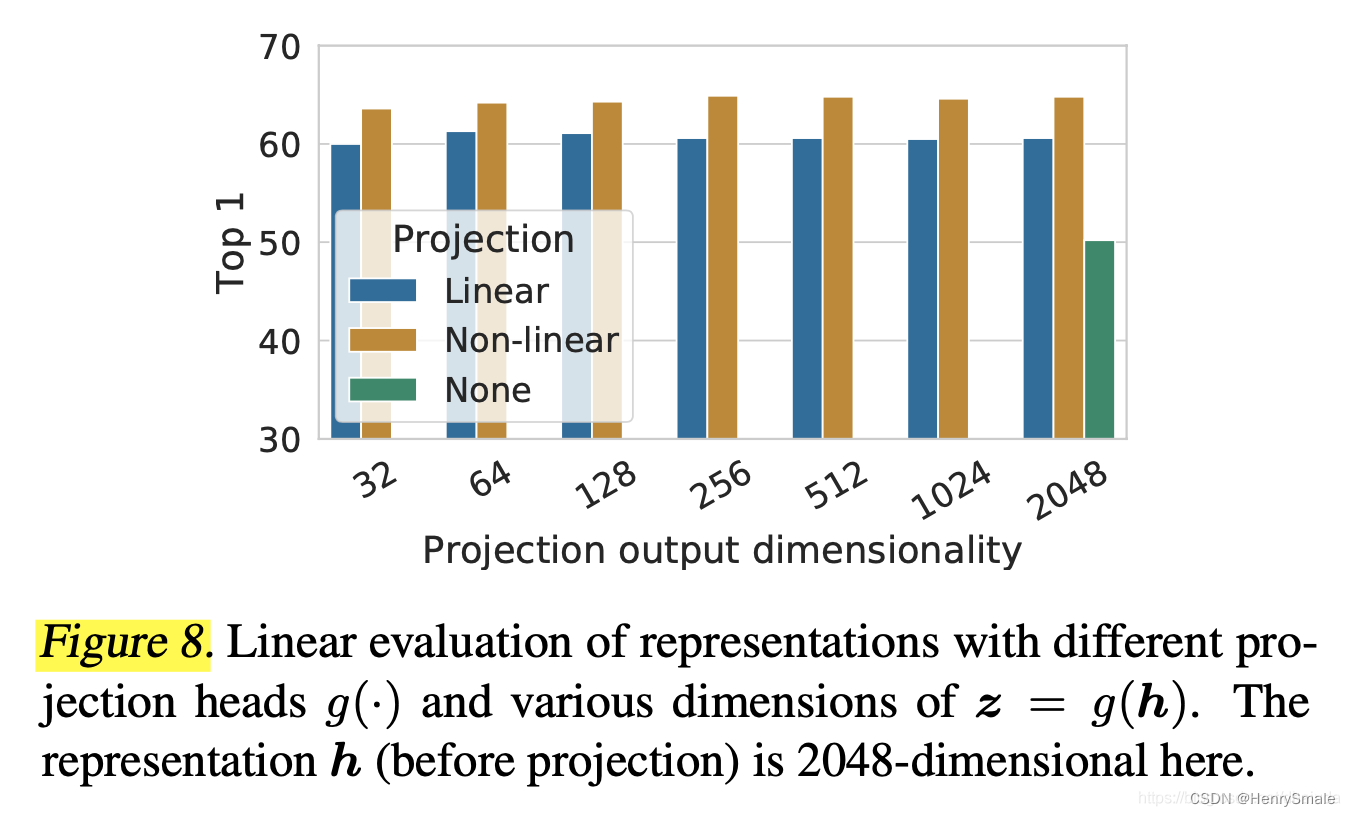
从图上可以得到如下结论：

• 向量长度对性能影响不大；
• 非线性MLP性能优于线性MLP；
• SimCLR中可以用于线性分类的特征有两个，一是特征提取器的输出$\mathbf{h}$，二是MLP层的输出$g(\mathbf{h})$，在线性分类中，使用$\mathbf{h}$的性能要优于$g(\mathbf{h})$(大于10%)，可能是因为MLP过滤掉了一些有用的信息。

3.4 batch size对性能的影响

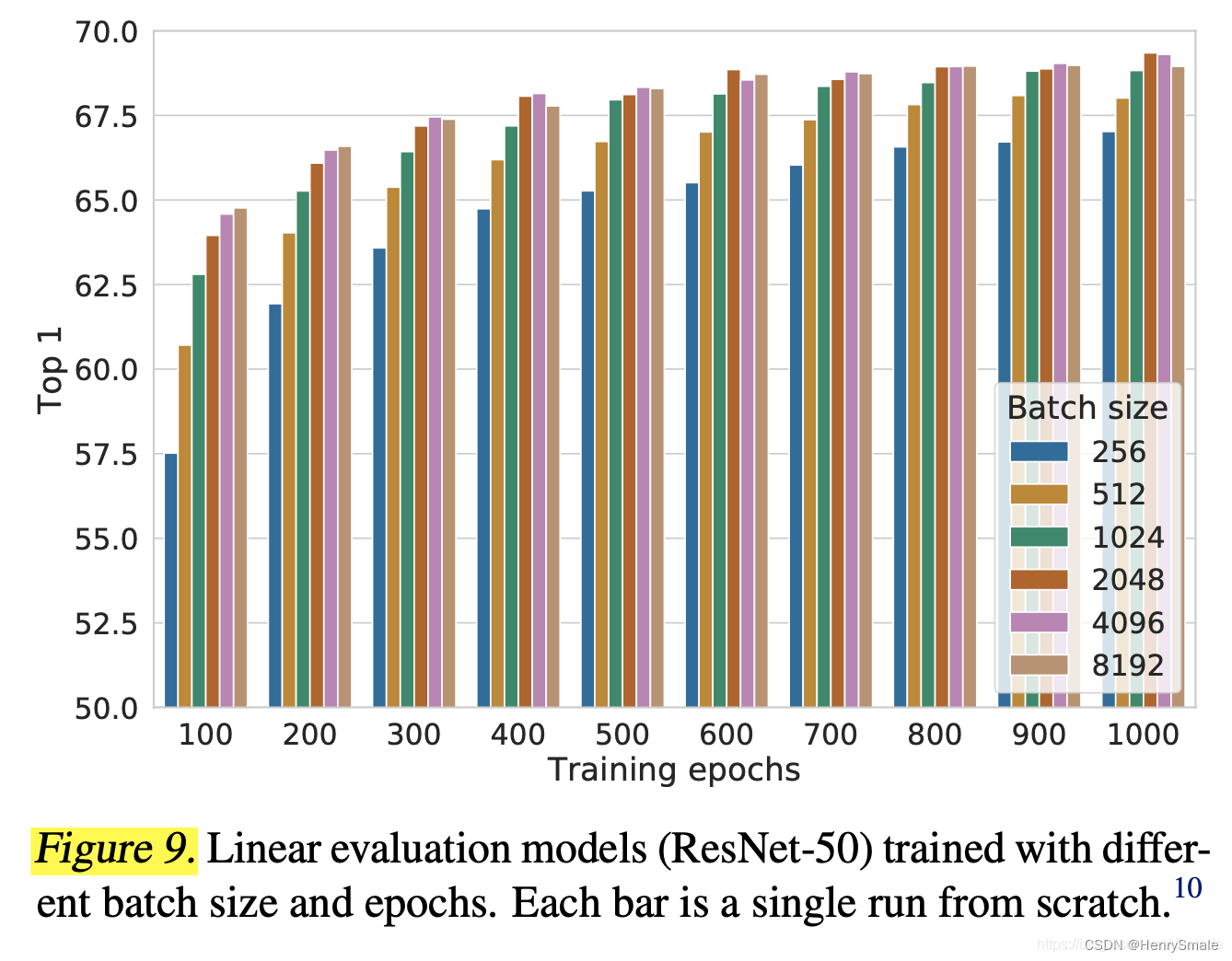
从图上可以得到如下结论：

• 对于有正负例的对比学习算法而言，batch size越大，效果越好，并且提升显著；
• 如果只有正例的对比学习算法而言(如BYOL、simsiam)，batch size大小对性能影响没有如此显著；
• 对于有正负例的对比学习算法和只有正例的对比学习算法，训练epoch越长，效果越好。