定义
感知机:假设输入控件(特征空间)是
X
⊆
R
n
\mathcal{X} \subseteq \mathbb{R}^n
X⊆Rn,输出空间是
Y
=
{
+
1
,
−
1
}
\mathcal{Y}=\left\{+1, -1\right\}
Y={+1,−1},输入
x
∈
X
\mathbf{x}\in\mathcal{X}
x∈X表示实例的特征向量,对应于输入空间(特征空间)的点;输出
y
∈
Y
y\in\mathcal{Y}
y∈Y表示实例的类别。由输入空间到输出空间的如下函数
f
(
x
)
=
s
i
g
n
(
w
⋅
x
+
b
)
f\left(\mathbf{x}\right) = \rm{sign}\left(\mathbf{w}\cdot \mathbf{x} + b\right)
f(x)=sign(w⋅x+b)
称为感知机,其中
w
\mathbf{w}
w和
b
b
b为感知机参数
s
i
g
n
(
x
)
=
{
+
1
,
x
≥
0
−
1
,
x
<
0
\rm{sign}\left(x\right) = \begin{cases} +1, & x\ge 0\\ -1, & x < 0 \end{cases}
sign(x)={+1,−1,x≥0x<0
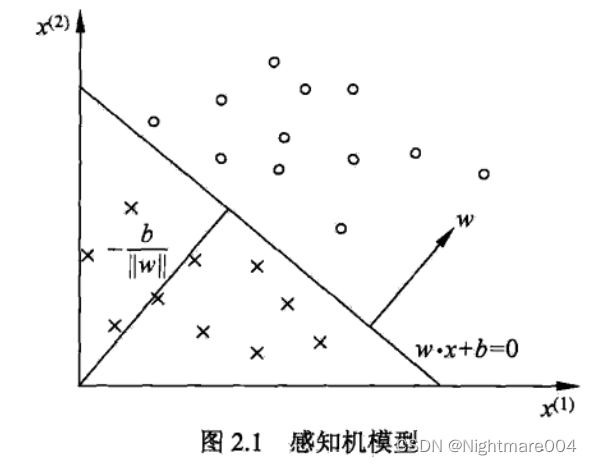
学习策略
数据集的线性可分性
给定一个数据集
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
T = \left\{\left(\mathbf{x}_1, y_1\right), \left(\mathbf{x}_2, y_2\right),\cdots, \left(\mathbf{x}_N, y_N\right)\right\}
T={(x1,y1),(x2,y2),⋯,(xN,yN)}
其中
x
i
∈
X
=
R
n
,
y
i
∈
Y
=
{
+
1
,
−
1
}
\mathbf{x}_i \in \mathcal{X} = \mathbb{R}^n, y_i\in\mathcal{Y} = \left\{+1, -1\right\}
xi∈X=Rn,yi∈Y={+1,−1}
如果存在某个超平面
S
S
S
w
⋅
x
+
b
=
0
\mathbf{w}\cdot \mathbf{x} + b = 0
w⋅x+b=0
能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧,即对所有
y
i
=
+
1
y_i = +1
yi=+1的实例
i
i
i,有
w
⋅
x
i
+
b
>
0
\mathbf{w}\cdot \mathbf{x}_i + b > 0
w⋅xi+b>0;对所有
y
i
=
−
1
y_i = -1
yi=−1的实例
i
i
i,有
w
⋅
x
i
+
b
<
0
\mathbf{w}\cdot \mathbf{x}_i + b <0
w⋅xi+b<0,则称数据集
T
T
T为线性可分数据集(linearly separable data set),否则,称数据集
T
T
T线性不可分
学习策略
假设训练数据集是线性可分的,感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。
感知机所采用的损失函数是误分类点到超平面 S S S的总距离。
首先输入空间
R
n
\mathbf{R}^n
Rn中任一点
x
0
\mathbf{x}_0
x0到超平面的距离:
1
∥
w
∥
∣
w
⋅
x
0
+
b
∣
\frac{1}{\|\mathbf{w}\|} \left|\mathbf{w}\cdot \mathbf{x}_0 + b\right|
∥w∥1∣w⋅x0+b∣
其次,对于误分类数据
(
x
i
,
y
i
)
\left(\mathbf{x}_i, y_i\right)
(xi,yi)来说,
−
y
i
(
w
⋅
x
i
+
b
)
>
0
-y_i\left(\mathbf{w}\cdot \mathbf{x}_i + b\right) > 0
−yi(w⋅xi+b)>0
因此,误分类点
x
i
\mathbf{x}_i
xi到超平面
S
S
S的距离是
−
1
∥
w
∥
y
i
(
w
⋅
x
i
+
b
)
-\frac{1}{\|\mathbf{w}\|}y_i\left(\mathbf{w}\cdot \mathbf{x}_i + b\right)
−∥w∥1yi(w⋅xi+b)
假设超平面
S
S
S的误分类点集合为
M
M
M, 那么所有误分类点到超平面
S
S
S的总距离为
−
1
∥
w
∥
∑
x
i
∈
M
y
i
(
w
⋅
x
i
+
b
)
-\frac{1}{\|\mathbf{w}\|}\sum_{\mathbf{x}_i\in M}y_i\left(\mathbf{w}\cdot \mathbf{x}_i + b\right)
−∥w∥1xi∈M∑yi(w⋅xi+b)
不考虑
1
∥
w
∥
\frac{1}{\|\mathbf{w}\|}
∥w∥1,就是感知机学习的损失函数
给定训练数据
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
T = \left\{\left(\mathbf{x}_1, y_1\right), \left(\mathbf{x}_2, y_2\right),\cdots, \left(\mathbf{x}_N, y_N\right)\right\}
T={(x1,y1),(x2,y2),⋯,(xN,yN)}
其中
x
i
∈
X
=
R
n
,
y
i
∈
Y
=
{
+
1
,
−
1
}
\mathbf{x}_i \in \mathcal{X} = \mathbb{R}^n, y_i\in\mathcal{Y} = \left\{+1, -1\right\}
xi∈X=Rn,yi∈Y={+1,−1}
感知机
s
i
g
n
(
w
⋅
x
+
b
)
\rm{sign}\left(\mathbf{w}\cdot \mathbf{x} + b\right)
sign(w⋅x+b)学习的损失函数定义为
L
(
w
,
b
)
=
−
∑
x
i
∈
M
y
i
(
w
⋅
x
i
+
b
)
L\left(\mathbf{w}, b\right) = -\sum_{\mathbf{x}_i \in M} y_i\left(\mathbf{w}\cdot \mathbf{x}_i + b\right)
L(w,b)=−xi∈M∑yi(w⋅xi+b)
其中
M
M
M为误分类点的集合
感知机学习算法
原始形式
给定训练数据
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
T = \left\{\left(\mathbf{x}_1, y_1\right), \left(\mathbf{x}_2, y_2\right),\cdots, \left(\mathbf{x}_N, y_N\right)\right\}
T={(x1,y1),(x2,y2),⋯,(xN,yN)}
其中
x
i
∈
X
=
R
n
,
y
i
∈
Y
=
{
+
1
,
−
1
}
\mathbf{x}_i \in \mathcal{X} = \mathbb{R}^n, y_i\in\mathcal{Y} = \left\{+1, -1\right\}
xi∈X=Rn,yi∈Y={+1,−1}
求参数
w
,
b
\mathbf{w}, b
w,b,使其为一下损失函数极小化问题的解
min
L
(
w
,
b
)
=
−
∑
x
i
∈
M
y
i
(
w
⋅
x
i
+
b
)
\min L\left(\mathbf{w}, b\right) = -\sum_{\mathbf{x}_i \in M} y_i\left(\mathbf{w}\cdot \mathbf{x}_i + b\right)
minL(w,b)=−xi∈M∑yi(w⋅xi+b)
其中
M
M
M为误分类点的集合
感知机学习算法是误分类驱动的,具体采用随机梯度下降法
首先任取一个超平面
w
0
,
b
0
\mathbf{w}_0, b_0
w0,b0,然后采用梯度下降法不断极小化目标函数
极小化过程中不是一次使
M
M
M中所有的误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降
∇ w L = − ∑ x i ∈ M y i x i ∇ b L = − ∑ x i ∈ M y i \nabla_{\mathbf{w}} L = -\sum_{\mathbf{x}_i \in M}y_i\mathbf{x}_i\\ \nabla_{b} L = -\sum_{\mathbf{x}_i \in M}y_i\\ ∇wL=−xi∈M∑yixi∇bL=−xi∈M∑yi
感知机学习算法的原始形式
输入:
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
T = \left\{\left(\mathbf{x}_1, y_1\right), \left(\mathbf{x}_2, y_2\right),\cdots, \left(\mathbf{x}_N, y_N\right)\right\}
T={(x1,y1),(x2,y2),⋯,(xN,yN)},其中
x
i
∈
X
=
R
n
,
y
i
∈
Y
=
{
+
1
,
−
1
}
\mathbf{x}_i \in \mathcal{X} = \mathbb{R}^n, y_i\in\mathcal{Y} = \left\{+1, -1\right\}
xi∈X=Rn,yi∈Y={+1,−1};学习率
η
(
0
<
η
≤
1
)
\eta\left(0 < \eta \le 1\right)
η(0<η≤1)
输出:
w
,
b
\mathbf{w}, b
w,b;感知机模型
f
(
x
)
=
s
i
g
n
(
w
⋅
x
+
b
)
f\left(x\right) = \rm{sign} \left(\mathbf{w}\cdot \mathbf{x} + b\right)
f(x)=sign(w⋅x+b)
(1)选取初始值
w
0
,
b
0
\mathbf{w}_0, b_0
w0,b0
(2)在训练中选取数据集
(
x
i
,
y
i
)
\left(\mathbf{x}_i, y_i\right)
(xi,yi)
(3)如果
y
i
(
w
⋅
x
+
b
)
≤
0
y_i\left(\mathbf{w}\cdot\mathbf{x} + b\right) \le 0
yi(w⋅x+b)≤0
w
←
w
+
η
y
i
x
i
b
←
b
+
η
y
i
\mathbf{w} \leftarrow \mathbf{w} + \eta y_i \mathbf{x}_i\\ b \leftarrow b + \eta y_i
w←w+ηyixib←b+ηyi
(4)转至(2)直至训练集中没有误分类点
根据选择错误点的顺序,得到的结果可能也不同
收敛性
记
w
^
=
(
w
b
)
,
x
^
=
(
x
1
)
\hat{\mathbf{w}} = \begin{pmatrix}\mathbf{w}\\b\\\end{pmatrix}, \hat{\mathbf{x}} = \begin{pmatrix}\mathbf{x}\\1\\\end{pmatrix}
w^=(wb),x^=(x1)
因此
w
^
⋅
x
^
=
w
⋅
x
+
b
\hat{\mathbf{w}}\cdot \hat{\mathbf{x}} = \mathbf{w} \cdot \mathbf{x} + b
w^⋅x^=w⋅x+b
Novikoff定理:设训练集
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
T = \left\{\left(\mathbf{x}_1, y_1\right), \left(\mathbf{x}_2, y_2\right),\cdots, \left(\mathbf{x}_N, y_N\right)\right\}
T={(x1,y1),(x2,y2),⋯,(xN,yN)}线性可分,其中
x
i
∈
X
=
R
n
,
y
i
∈
Y
=
{
+
1
,
−
1
}
\mathbf{x}_i \in \mathcal{X} = \mathbb{R}^n, y_i\in\mathcal{Y} = \left\{+1, -1\right\}
xi∈X=Rn,yi∈Y={+1,−1}
(1)存在满足条件
∥
w
^
o
p
t
∥
=
1
\|\hat{\mathbf{w}}_{opt}\| = 1
∥w^opt∥=1的超平面
w
^
o
p
t
⋅
x
^
=
0
\hat{\mathbf{w}}_{opt} \cdot \hat{\mathbf{x}} =0
w^opt⋅x^=0将训练数据集完全正确分开;且存在
γ
>
0
\gamma > 0
γ>0使得
y
i
(
w
^
o
p
t
⋅
x
^
i
)
≥
γ
y_i \left(\hat{\mathbf{w}}_{opt} \cdot \hat{\mathbf{x}}_i\right)\ge \gamma
yi(w^opt⋅x^i)≥γ
(2)令
R
=
max
1
≤
i
≤
N
∥
x
^
i
∥
R = \max\limits_{1 \le i \le N}\|\hat{\mathbf{x}}_i\|
R=1≤i≤Nmax∥x^i∥,则感知机算法在训练数据集上的误分类次数
k
k
k满足
k
≤
(
R
γ
)
2
k \le \left(\frac{R}{\gamma}\right)^2
k≤(γR)2
证明:
(1)由线性可分的定义,显然存在满足条件
∥
w
^
o
p
t
∥
=
1
\|\hat{\mathbf{w}}_{opt}\| = 1
∥w^opt∥=1的超平面
w
^
o
p
t
⋅
x
^
=
0
\hat{\mathbf{w}}_{opt} \cdot \hat{\mathbf{x}} =0
w^opt⋅x^=0
令
γ
=
min
i
y
i
(
w
^
o
p
t
⋅
x
^
i
)
\gamma = \min\limits_{i} y_i \left(\hat{\mathbf{w}}_{opt} \cdot \hat{\mathbf{x}}_i\right)
γ=iminyi(w^opt⋅x^i),结论成立
(2)
设
w
^
0
=
0
\hat{\mathbf{w}}_0 = \mathbf{0}
w^0=0,如果实例被误分类,则更新权重
令
w
^
k
−
1
\hat{\mathbf{w}}_{k-1}
w^k−1使第
k
k
k个误分类实例之前的权重,则
y
i
(
w
^
k
−
1
)
⋅
x
^
i
≤
0
y_i\left(\hat{\mathbf{w}}_{k-1}\right) \cdot \hat{\mathbf{x}}_i \le 0
yi(w^k−1)⋅x^i≤0
并且
w
^
k
=
w
^
k
−
1
+
η
y
i
x
^
i
\hat{\mathbf{w}}_k = \hat{\mathbf{w}}_{k-1} + \eta y_i\hat{\mathbf{x}}_i
w^k=w^k−1+ηyix^i
w ^ k ⋅ w ^ o p t = w ^ k − 1 ⋅ w ^ o p t + η y i ( x ^ i ⋅ w ^ o p t ) ≥ w ^ k − 1 ⋅ w ^ o p t + η γ ≥ k η γ \begin{aligned} \hat{\mathbf{w}}_k \cdot \hat{\mathbf{w}}_{opt} &= \hat{\mathbf{w}}_{k-1}\cdot \hat{\mathbf{w}}_{opt} + \eta y_i\left(\hat{\mathbf{x}}_i\cdot \hat{\mathbf{w}}_{opt}\right)\\ &\ge\hat{\mathbf{w}}_{k-1}\cdot \hat{\mathbf{w}}_{opt} + \eta\gamma\\ &\ge k\eta\gamma \end{aligned} w^k⋅w^opt=w^k−1⋅w^opt+ηyi(x^i⋅w^opt)≥w^k−1⋅w^opt+ηγ≥kηγ
根据
y
i
(
w
^
k
−
1
)
⋅
x
^
i
≤
0
y_i\left(\hat{\mathbf{w}}_{k-1}\right) \cdot \hat{\mathbf{x}}_i \le 0
yi(w^k−1)⋅x^i≤0,有
∥
w
^
k
∥
2
=
∥
w
^
k
−
1
∥
2
+
2
η
y
i
(
w
^
k
−
1
⋅
x
^
i
)
+
η
2
y
i
2
∥
x
^
i
∥
2
=
∥
w
^
k
−
1
∥
2
+
2
η
y
i
(
w
^
k
−
1
⋅
x
^
i
)
+
η
2
∥
x
^
i
∥
2
≤
∥
w
^
k
−
1
∥
2
+
η
2
∥
x
^
i
∥
2
≤
∥
w
^
k
−
1
∥
2
+
η
2
R
2
≤
k
η
2
R
2
\begin{aligned} \|\hat{\mathbf{w}}_k\|^2 &= \|\hat{\mathbf{w}}_{k-1}\|^2 + 2\eta y_i \left(\hat{\mathbf{w}}_{k-1}\cdot \hat{\mathbf{x}}_i\right) + \eta^2 y_i^2 \|\hat{\mathbf{x}}_i\|^2\\ &= \|\hat{\mathbf{w}}_{k-1}\|^2 + 2\eta y_i \left(\hat{\mathbf{w}}_{k-1}\cdot \hat{\mathbf{x}}_i\right) + \eta^2 \|\hat{\mathbf{x}}_i\|^2\\ &\le \|\hat{\mathbf{w}}_{k-1}\|^2 + \eta^2 \|\hat{\mathbf{x}}_i\|^2\\ &\le \|\hat{\mathbf{w}}_{k-1}\|^2 + \eta^2 R^2\\ &\le k \eta^2 R^2 \end{aligned}
∥w^k∥2=∥w^k−1∥2+2ηyi(w^k−1⋅x^i)+η2yi2∥x^i∥2=∥w^k−1∥2+2ηyi(w^k−1⋅x^i)+η2∥x^i∥2≤∥w^k−1∥2+η2∥x^i∥2≤∥w^k−1∥2+η2R2≤kη2R2
因此
k
η
γ
≤
w
^
k
⋅
w
^
o
p
t
≤
∥
w
^
k
∥
∥
w
^
o
p
t
∥
=
∥
w
^
k
∥
≤
k
η
R
k\eta \gamma \le \hat{\mathbf{w}}_k \cdot \hat{\mathbf{w}}_{opt} \le \|\hat{\mathbf{w}}_k \|\| \hat{\mathbf{w}}_{opt}\|=\|\hat{\mathbf{w}}_k \|\le \sqrt{k} \eta R
kηγ≤w^k⋅w^opt≤∥w^k∥∥w^opt∥=∥w^k∥≤kηR
因此
k
≤
(
R
γ
)
2
k \le \left(\frac{R}{\gamma}\right)^2
k≤(γR)2
参考:
统计学习方法(李航)
https://www.cntofu.com/book/48/gan-zhi-xue-xi-ji.md
https://zhuanlan.zhihu.com/p/361176523