问题介绍

根据表1、2、3 所列数据，以能耗、运行时间、舒适性为目标分别设计列车运行速度—距离曲线；完成单目标以及多目标优化下的列车运行对比；选择其中一种方案，设计列车速度跟踪控制算法并进行性能分析。

                                 1 列车参数设置表

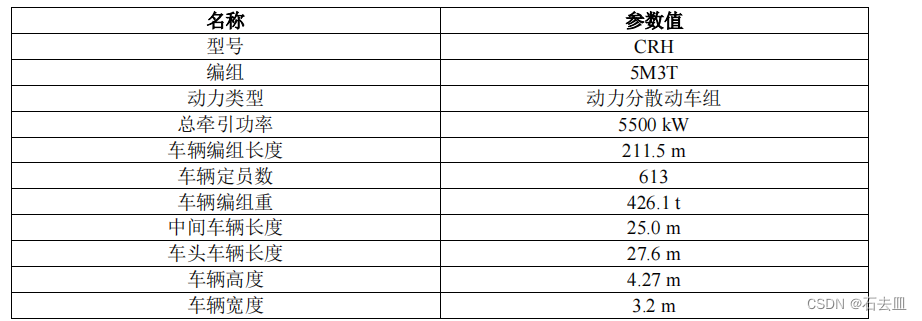
在这里插入图片描述

优化算法选择：

PSO算法使用粒子群来搜索问题的最佳解决方案。每个粒子表示问题的候选解决方案，粒子在搜索空间中的位置表示解决方案。PSO算法使用“适合度”的概念来评估候选解决方案的质量。粒子的适应度是根据需要优化的目标函数计算的。

MOPSO算法是多目标粒子群优化算法的一种，其主要思想是通过维护一组非支配解（Pareto 最优解集）来实现多目标优化。

问题建模与编码及结果

路况表示

路况包括线路的限速值和线路的坡度，以及其它的参数。本文只考虑限速和坡度。
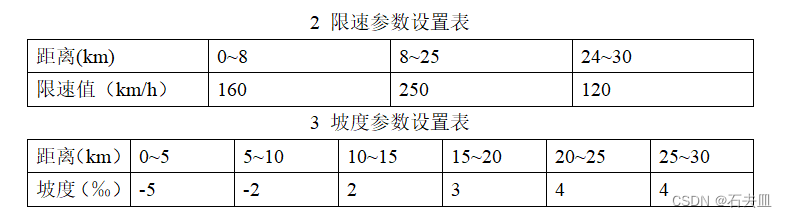
一般的限速曲线是直角的如图示红线，这个曲线是根据限速值（160km/h,250km/h,120km/h）生成的，它将km/h变化单位为m/s。图示横坐标单位为m，纵坐标单位为m/s。
但如果直接使用红线作为限速曲线，当需要减速时，可能减速较晚，导致列车制动力不足以使列车减速到指定限速值，就会越过曲线，发生危险。
因此我们找到了一种基于制动的限速曲线，如图所示。在限速曲线发生下降的地方，充分考虑列车的制动情况，保证列车在紧挨制动曲线运行时，紧急制动可以将列车安全制动，而不会超过线路实际限速值。
同时，底部的曲线的是线路的坡度（-5,-2,2,3,4,4）。因此下图就是线路包含限速和坡度的路况。
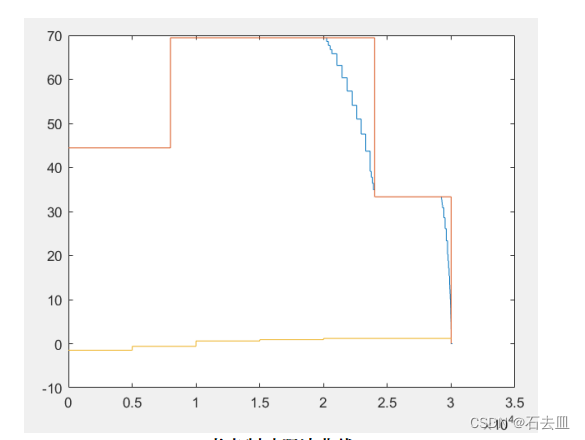
在这里插入图片描述

工况表示

轨道交通系统的控制几乎是提前设定好了的，而且在这个控制过程中如何减少能量的消耗才是最关键的目的。列车在站间运行时会根据线路条件、自身列车特性、前方线路状况计算出一个限制速度。列车运行过程中不允许超过此限制速度。限制速度会周期性更新。在限制速度的约束下列车通常包含四种运行工况：牵引、巡航、惰行和制动。
牵引阶段：列车加速，发动机处于耗能状态。
巡航阶段：列车匀速，列车所受合力为0，列车是需要牵引还是需要制动取决于列车当时受到的总阻力。
惰行阶段：列车既不牵引也不制动，列车运行状态取决于受到的列车总阻力，发动机不耗能。
制动阶段：列车减速，发动机不耗能。如果列车采用再生制动技术，此时可以将动能转换为电能反馈回供电系统供其他用电设备使用，例如其他正在牵引的列车或者本列车的空调等（本列车空调的耗能较小，通常忽略不计）。
因此要提前设计好控制策略，如代码所示，先进行牵引（2）然后巡航（1），之后惰行（0），然后从160km/h的限速达到了250km/h的区段，再进行新一轮的牵引（2）然后巡航（1），之后惰行（0），之后进行制动（-2）到达限速为120km/h的区段，然后惰行一段距离（0），最后减速进站（-2），完成控制。因此代码中stateTable=[2,1,0,2,1,0,-2,0,-2]。而解的上限和解的下限就是需要在这个上限与下限区间内完成工况的转换，具体的转换点是在这个区间随机生成的。

列车牵引力

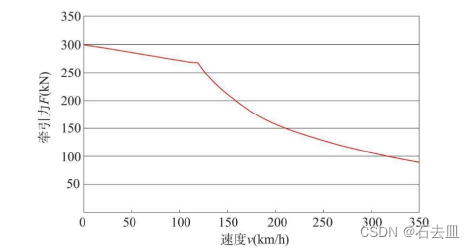
在这里插入图片描述

阻力

制动力

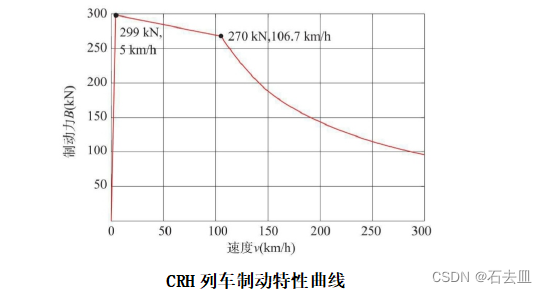
在这里插入图片描述

目标函数

在这里插入图片描述

粒子群算法设置

保证精度的基础上最大程度保证速度，设置种群大小10，最大迭代次数为10。

单目标优化（能耗/时间/舒适度）

运行图示例

在这里插入图片描述

单目标优化结果

在以能耗为优化目标时，能耗消耗最少。在以时间为优化目标时，时间消耗最少。在以舒适度为优化目标时，舒适度达到较好的程度（舒适度值最小）
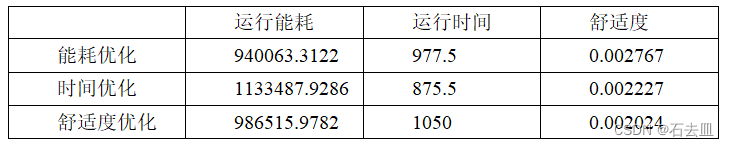
在这里插入图片描述

多目标优化

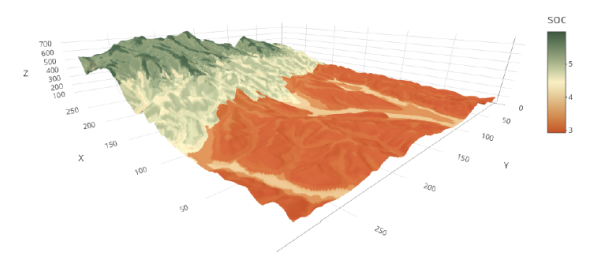
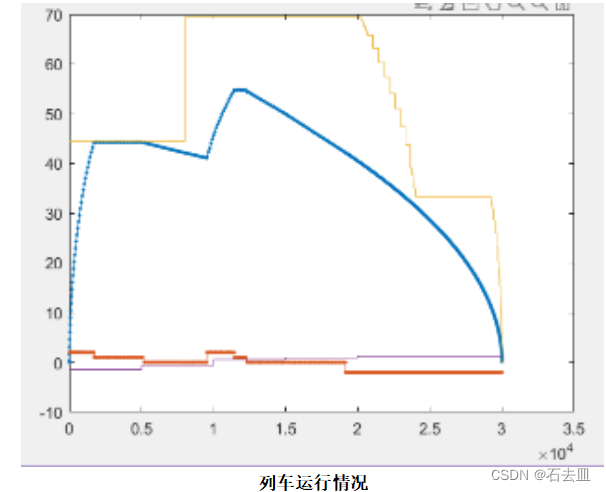
下图是列车在30km的区间的运行状况，横坐标是距离，单位为m，纵坐标为速度，单位m/s。可以看到最上面的曲线是改进后的限速曲线，蓝色曲线是粒子群算法根据能量、时间、舒适度为多目标优化出来的速度距离曲线，列车在这种路况和工况下，按照这个曲线行驶，能耗、时间、舒适度会达到一种较好并且均衡的状态。下面紫色的细线是线路坡度，红色的线则是工况状态。

在这里插入图片描述

总结

以能耗、运行时间、舒适性为目标分别设计列车运行速度—距离曲线；完成单目标以及多目标优化下的列车运行对比；
第一，首先建立列车模型（受力、控制工况）和道路模型（限速、坡度），并把模型用代码进行表示。然后分别以能耗、运行时间、舒适性为目标，通过基本的粒子群算法，设计出列车运行速度-距离曲线。通过优化速度曲线，可以达到降低能耗、缩短运行时间或者保障乘客的舒适体验的目标，并且最终的数据也验证了这一点。
第二，我们在单目标优化的基础上进行了基于MOPSO算法,并在能耗、运行时间、舒适性维度上进行了对比。通过对比实验，我们可以评估不同优化目标对列车运行方案的影响，进一步优化列车运行策略，以达到更加理想的效果。