开发中遇到一个问题,二维空间里正方形,按p点旋转90度后的点A2点的坐标是多少,这个设计到三角函数和矩阵的运算下面有公式。
由此翻了一遍三角函数相关的知识:
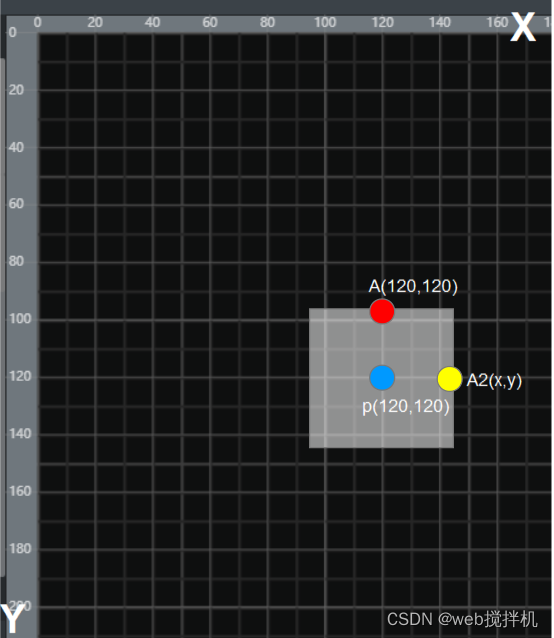
A点绕p点旋转90度得A2点的坐标是多少,用三角函数解答:
//计算公式
var angleInRadians = angleInDegrees * Math.PI / 180;
var s = Math.sin(angleInRadians);
var c = Math.cos(angleInRadians);扩展知识:WebGL 二维旋转
X坐标:
Math.cos(((Math.PI / 180) * 90)).toFixed(1)*(120-120)- Math.sin(((Math.PI / 180) * 90)).toFixed(1)*(100-120)+120;
//140
Y坐标:
Math.sin(((Math.PI / 180) * 90)).toFixed(1)*(120-120)+ Math.cos(((Math.PI / 180) * 90)).toFixed(1)*(100-120)+120;
//140三角函数对照表
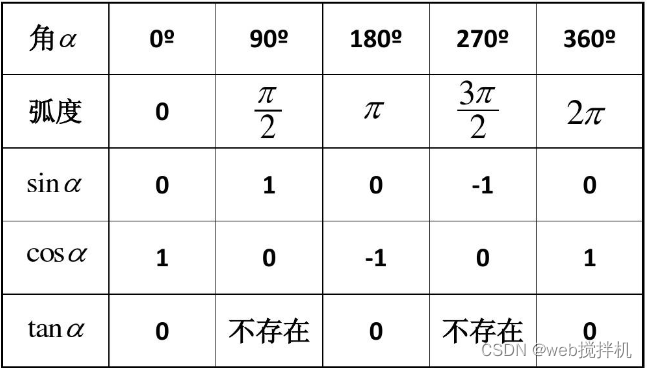
JavaScript中的三角函数计算
Math.sin(((Math.PI / 180) * 0)).toFixed(1) //sin:0 ——0
Math.sin(((Math.PI / 180) * 30)).toFixed(1) //sin:30 ——0.49999999999999994
Math.sin(((Math.PI / 180) * 45)).toFixed(1) //sin:45 ——0.7071067811865475
Math.sin(((Math.PI / 180) * 60)).toFixed(1) //sin:60 ——0.8660254037844386
Math.sin(((Math.PI / 180) * 90)).toFixed(1) //sin:90 ——1
Math.sin(((Math.PI / 180) * 180)).toFixed(1) //sin:180 ——1.2246467991473532e-16
Math.sin(((Math.PI / 180) * 270)).toFixed(1) //sin:270 ——-1
Math.sin(((Math.PI / 180) * 360)).toFixed(1) //sin:360 ——-2.4492935982947064e-16
Math.cos(((Math.PI / 180) * 0)).toFixed(1) //cos:0 ——1
Math.cos(((Math.PI / 180) * 30)).toFixed(1) //cos:30 ——0.8660254037844387
Math.cos(((Math.PI / 180) * 45)).toFixed(1) //cos:45 ——0.7071067811865476
Math.cos(((Math.PI / 180) * 60)).toFixed(1) //cos:60 ——0.5000000000000001
Math.cos(((Math.PI / 180) * 90)).toFixed(1) //cos:90 ——6.123233995736766e-17
Math.cos(((Math.PI / 180) * 180)).toFixed(1) //cos:180 ——-1
Math.cos(((Math.PI / 180) * 270)).toFixed(1) //cos:270 ——-1.8369701987210297e-16
Math.cos(((Math.PI / 180) * 360)).toFixed(1) //cos:360 ——1含有科学计数法的值无限接近于0

sin:180 ——1.2246467991473532e-16
sin:360 ——-2.4492935982947064e-16
cos:90 ——6.123233995736766e-17
cos:270 ——-1.8369701987210297e-16
为什么math.cos(90*math.pi/180)生成6.123031769111…而不是零?

大概意思:

三角函数与矩阵应用
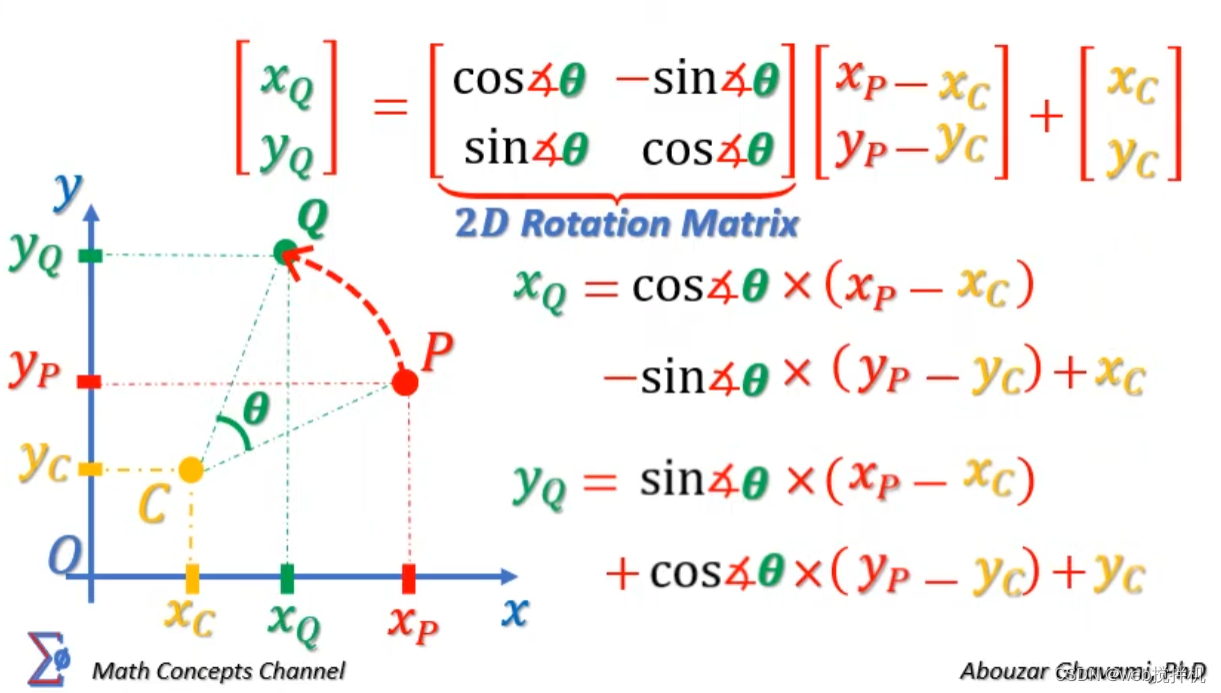
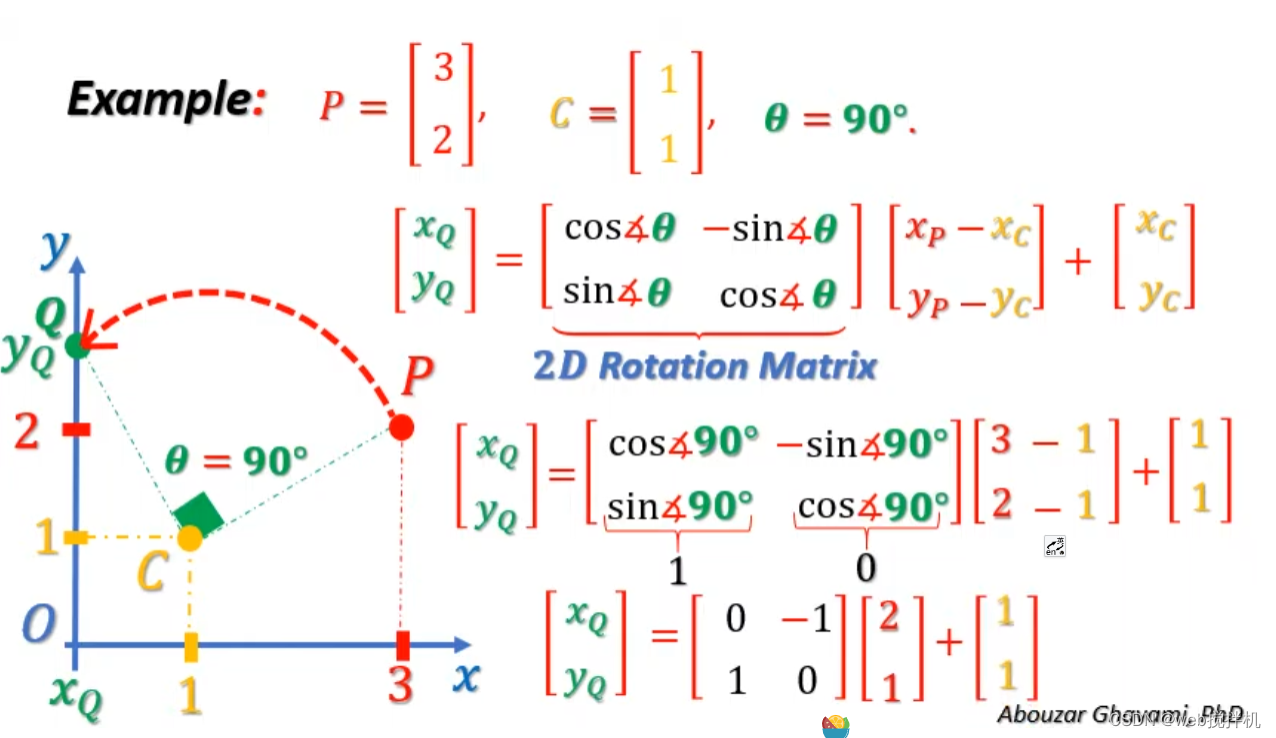

油管地址:https://www.youtube.com/watch?v=JG2C_Pf5V1w











![[Spring]初始导读](https://img-blog.csdnimg.cn/3d146fc95f02453a948cdc8e7ef47a40.png)