前言
本文教程均来自b站【小白也能听懂的人工智能原理】,感兴趣的可自行到b站观看。
本文【原文】章节来自课程的对白,由于缺少图片可能无法理解,故放到了最后,建议直接看代码(代码放到了前面)。
代码实现
dataset.py
import numpy as np
def get_beans(counts):
xs = np.random.rand(counts)
xs = np.sort(xs)
ys = np.array([1.2*x+np.random.rand()/10 for x in xs])
return xs,ys
import dataset
import numpy as np
from matplotlib import pyplot as plt
## Create a dataset
n = 100
xs, ys = dataset.get_beans(n)
# 配置图像
plt.title("Size-Toxicity Function",fontsize=12)
plt.xlabel("Bean Size")
plt.ylabel("Toxicity")
plt.scatter(xs,ys)
w=0.1
y_pre=w*xs
plt.plot(xs,y_pre)
plt.show()
# 随机梯度下降法
def gsd(w=0.1):
# 在全部样本上做50次梯度下降
for _ in range(50):
for i in range(100):
x = xs[i]
y = ys[i]
# a=x^2
# b=-2*x*y
# c=y^2
# 斜率k=2aw+b
k = 2 * (x ** 2) * w + (-2 * x * y)
alpha = 0.1
w = w - alpha * k # w根据梯度下降的方向走,如w此时的k<0,则w处于抛物线左端,应该往右边走,相反则往左边走
# 绘制动态变化的曲线
plt.clf() # 清空窗口
plt.scatter(xs, ys)
y_pre = w * xs
# 限制x轴和y轴的范围,使之不自动调整,避免图像抖动
plt.xlim(0, 1)
plt.ylim(0, 1.2)
plt.plot(xs, y_pre)
plt.pause(0.01) # 暂停0.01s,因为不暂停的话会无法显示
# 批量梯度下降 事实上 batchGSD()和gsd()方法是一样的,不过batchGSD()方法用了numpy.sum运算更加快速
def batchGSD(w=0.1):
alpha=0.1
for _ in range(100):
# 代价函数:e=(y-w*x)^2=x^2*w^2+(-2x*y)*w+y^2
# a=x^2
# b=-2x*y
# 求解斜率:k=2aw+b
k=2*np.sum(xs**2)*w+np.sum(-2*xs*ys)
k=k/100 # 100个豆豆,求得平均方差代价
w=w-alpha*k
y_pre=w*xs
plt.clf()
plt.xlim(0,1)
plt.ylim(0,1.2)
plt.plot(xs,y_pre)
plt.scatter(xs,ys)
plt.pause(0.01)
# 非梯度下降的固定步长下降
def FixedStep(w=0.1):
alpha=0.1
step=0.01
for _ in range(500):
k=2*np.sum(xs**2)*w+np.sum(-2*xs*ys)
k=k/100
if k>0:
w=w-step
else:
w=w+step
y_pre=w*xs
plt.clf()
plt.xlim(0, 1)
plt.ylim(0, 1.2)
plt.plot(xs, y_pre)
plt.scatter(xs, ys)
plt.pause(0.01)
# 绘制最终散点图和预测曲线
# plt.scatter(xs,ys)
# y_pre=w*xs
# plt.plot(xs,y_pre)
# plt.show()
# 随机梯度下降
gsd()
# 批量梯度下降
batchGSD()
# 非梯度下降的固定步长下降
FixedStep()
实验结果
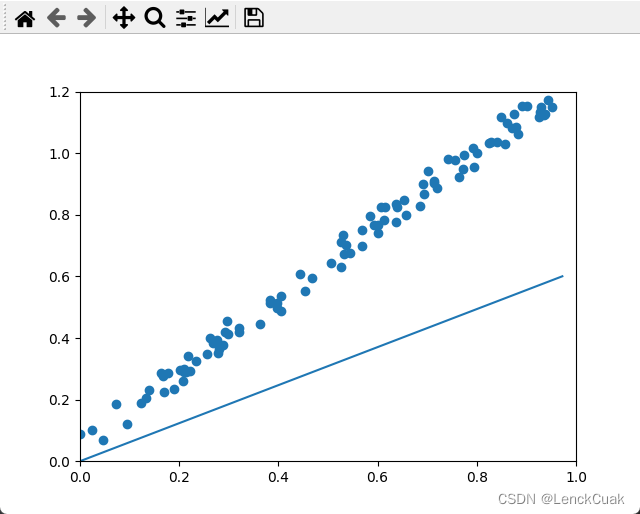

事实上三种方法的效果图是差不多的,所以只放出两张图
原文
上一节课我们通过顶点坐标公式求解出抛物线的最低点的w坐标,得到了让误差代价最小的w但是我们也通过算一笔账,说明了这种一步到位的求解方式固然是好,但是在输入特征过多,样本数量过大的时候却非常消耗计算资源。现在我们就来看看另外一种更加常用的方法,其实在上节课的讲解中也暗示了这一点我我们用了一个“挪”字来描述这个过程,抛物线最低点坐标的寻找过程其实不必一步到位,大可以采用一点点挪动的方式,比如一开始w的值是2,误差是这么多,如果在这里画一个球,那要到达最低点,需要向左滑落,而不是向右攀升,如果w等于0.6,要到达最低点,需要向右滑落,而不是向左攀升,这规律就很明显了。在最低点的左边需要不断的把w调大。而在右边的时候不断的把w调小。
而具体实施起来也很方便,我们使用斜率一个开口向上抛物线的最低点的斜率是0,而左边的斜率是负数,右边的斜率是正数,所以现在我们的目的很明确,想办法得到代价函数曲线在当前w取值这个点上的斜率,这样我们就可以判断当前w取值是在最低点的左边还是在右边,然后不断去调整w直到到达最低点,也就是说得到一个让误差代价最小的w。我们之前已经证明了误差,e和w形成的代价函数是一个标准的一元二次函数。
有一回他对我说到,你读过书吗?我略略的点点头,他说读过书我便考你一,考这个一元二次函数的斜率怎样求的?我想讨饭一样的人也配考我,便回过脸去不再理会他,等了许久很恳切的说道,不能求吧我教给你记着这些方法,应该急着将来做程序员的时候写程序要用,有两样求法。
在遥远的过去,我们的祖先曾坚定不移的相信着天圆而地方,但自从麦哲伦完成环球航行,我们开始了解到地球其实是一个球,表面是一个曲面,我们之所以觉得大地是平直的,只是因为我们太过渺小。
在这个巨大的蓝色星球上,我们的先祖用脚能够丈量的范围相比于整个地球实在是微不足道。同样的道理,当我们看这个曲线的时候,它显而易见是弯的,我们此刻更像是上帝的视角看见了它的全部,而当我们盯着一个点不断的变小变小,当我们足够小的时候,同样显而易见的是曲线它是直的,这种值是宏观的弯曲在微观中的一种近似,而一个直线的斜率就十分好求了。我们取这个直线上的某个点,如果横坐标是w那么纵坐标e就是aw平方加bw加c我们再取附近右边的一个点,比如这个点和第一个点的横坐标的距离为灯塔w那么这一点的横坐标就是w加上德尔塔w纵坐标是a括号w加上德尔塔w括号平方加上b括号w加上德尔塔w括号加c那这个直线的斜率自然就是这两个点的纵坐标的差值除以横坐标的差值整理一下,结果是这样的。
这就是当我们作为一个极小的生物降落在曲线的一个点上计算出来的斜率,但要注意一点,我们既然在用直线的方法计算斜率,那么就必须保证两点之间的距离足够小,以保证足够近似一个直线。那该是多小呢?是相对于地球表面两个脚印之间的距离吗?不,这还不够小,要再小一点再小一点。那是分子或原子之间的距离吗?不也不是。其实这种无限小我们很难找到直观的物理表达,它更是一个数学上的概念极限,只有在曲线上一个点附近取一个距离无限接近的点的时候,用直线的方法计算的斜率才能成为这个点的真实斜率,我们不必去纠结这个无限小到底是多小,它只是一个数学上的概念和手段,当然这个概念也是微积分大厦的重要基石,我们用一个极限符号limit来表示极限的概念,当德尔塔w无穷小的时候,德尔塔w自然会歼灭,所以这个点的斜率就是2,aw加b在曲线中某数的斜率,我们一般把它称之为导数,或许你以前没有学过导数,但是现在你学过了用纵坐标的差值除以横坐标的差值并取极限,这其实也就是导数的定义了。
所以这种求导的方法也称之为定义法。实际上用定义法原则上可以求解出任意一个函数,任意一点的导数,不管它是这样这样还是这样,当然你需要仔细的小心的去做计算。既然说有两样方法那不如我们耐心听完。
第二种其实更加简单,计算的难度也更小一点。既然定义法可以得到一个函数的导数,而我们知道数学里常用的函数也就那么多,那我们全部求出来做成一张表格,形成固定的公式,然后用的时候去查询岂不美哉?没错,确实有人做出来了,但想想似乎又不对劲,虽然常用的函数就那么多,但是它们的组合却是无穷无尽的。
对于这些无穷无尽的组合喊出我们不可能用有限的生命投入到无限的事情中,毕竟传统功夫点到为止,当然我们总是能琢磨出一些新的规律,实际上不论怎样的函数组合都逃不脱三种基本的形式,加法、乘法和复合,什么还有减法和除法,那不过是加法和乘法的另外一种形式。
我们的方差代价函数就是一个明显的通过乘法和加法组合起来的函数,a乘以w的平方是一个长函数和一个幂函数的乘法长函数的导数查询公式可知等于0,幂函数的导数是把幂放到前面,再把幂减一,而利用导数的乘法法则,两个函数乘法的倒数是第一个函数的导数乘以第二个函数,再加上第二个函数的导数乘以第一个函数,所以结果是2,aw同样bw也是一个长函数和一个幂函数的乘法组合结果是b而c是一个长函数,导数是0,然后利用导数的加法法则,直接把这三个部分加在一起,最终的导数是2aw加b+0,你看这和用定义法得到的结果一模一样。
这个一元二次函数的斜率的两样求法我们都知道了,再回到这个问题本身,直观上来看,这其实也挺合理的。在直线中斜率是个常数,因为斜率一直没有变化,而在抛物线中斜率和自变量有关,如此我们也就可以知道代价函数曲线的每个点的斜率。
我们小蓝的神经元终于可以根据代价函数的斜率是否大于0来决定w的调整行为了。
那么问题又来了,每次调整多少合适?按照目前的经验和直觉来看,每次只能调一点点,不能调多累,不如我们就先试试,每次调整0.01。这样好像可以。但是我们发现下降的过程有点慢,在最低处还反复的震荡,因为不论当前w设计调整的幅度都是呆板的0.01,那有没有更聪明一点的方式呢?有,当w距离最低点比较远的时候,我们其实希望它能够快一点,而逐渐接近最低点的时候,我们希望它慢下来,这样就既能加快下降的速度,又能在最低点处稳如老狗。
这就好比给你一张图片,让你把图片中的这个圆形切割出来,一开始我们大刀阔斧的切,而越到后来越精雕细琢的切,这样要比每次呆板的切掉,固定的大小效率要好,精度还高。同时我们发现距离最低点越远的地方,这个斜率的绝对值越大,而越近的地方越小,当接近最低点的时候,这个值几乎为0,而最低点的斜率它就是0是分界点,而斜率在左右的符号又正好不同,这可太好了,刚好可以利用斜率的值来做这件事情,让w每次直接减去这个点的斜率的值。
如此当前w在右边的时候斜率是正数,w减去一个正数,像小调整在左边的时候斜率是负数,w减去一个负数向大调整,同时也做到了距离最低点比较远的时候,斜率大调整的多,大刀阔斧比较近的时候,斜率小调整的少,精雕细琢。
但是当我们打开代价函数调整的可视化工具运行一下这个调整过程的时候,你会发现此时此刻恰如彼时彼克在Rosenblatt感知器中做参数调整的时候,也发现发现了这个问题调整的过程太正当,无法收敛,但是没有关系,方法还是一样的,考虑给斜率也乘上一个比较小的学习率,阿尔法调和一下,比如阿尔法等于0.1,你看这次的调整过程变得又快,在最低点处又稳。
这种根据曲线不同处斜率去调整w的方式,也就是所谓的梯度下降,为什么叫梯度下降?而不是斜率下降,梯度是一个比斜率更加广泛的概念。在这里我们的代价函数是二维的,似乎说斜率也就够了,但后面说到更高维度的时候,斜率这个词就不太合适了,这里我们暂时就把梯度先理解为斜率,这样也可以。
而当我们经过多次剃度下降的过程后,w收敛到最低点附近,停止剃度下降的过程,把此时w作为预测模型中的w值,此时便能够相当准确的完成预测了。
到此我们终于可以回过头来去看看罗森布拉特感知器的参数调整方式了,它为什么好使?你会发现那正好是一个方差代价函数的斜率啊(除以2)。和我们这里的梯度下降如出一辙。
所以梯度下降和前面说的一步求解的正规方程相比,优势何在?我们一开始就讨论过单个样本的情况,它的代价函数是一个开口向上的抛物线,每个样本都是。之后我们又讨论了把所有样本合在一起的代价函数仍然是一个开口向上的抛物线,这个合成代价函数的最低点是整个样本的全局最优点,我们直接用全部样本进行梯度下降,你看这个下降的过程是一个明确且顺滑的轨迹,这也就是标准的梯度下降,也称之为批量梯度下降。
那如果我们每次只使用一个样本,这个样本的最低点不一定是全局最优,如果我们不断的依次在这些单样本代价函数上进行梯度下降,虽然会有震荡和波动。但是多次以后他们的整体趋势仍然会向全局最优点滑动,最后也可成功,而不像正规方程中那样一次性带入全部的样本进行计算,如果我们有海量的数据,你的机器b必然gg。这种每次取一个样本进行的梯度下降,因为其收敛的过程是一个随机震荡的轨迹,所以也称之为随机梯度下降。实际上最后在最低点附近这个震荡的轨迹是一个经典的布朗运动,批量有批量的好处可以并行计算,且更容易向全局最优点收敛,但是其缺点也是明显的,还是那个极端的例子,100万个数据要一次性计算出来,那么和正规方程也就没啥区别了,随机也有随机的好处,海量数据可以慢慢的来,每次都更新参数,参数的更新过程变得更快了,但是其缺点也是明显的无法并行计算,且不容易向全局最优点收敛。
所以综合二者的优缺点,我们又是向来喜欢折中的,人们往往采用一种调和的方法,mini batch梯度下降。每次选择全体样本中的一小批,比如100个、200个进行梯度下降,不得不说折中调和真是经久不衰的智慧,那到此为止,你也就了解了机器学习精髓之一的梯度下降。


![[Spring]初始导读](https://img-blog.csdnimg.cn/3d146fc95f02453a948cdc8e7ef47a40.png)