文章目录
- 位图的介绍
- 位图的引入
- 位图的概念
- 位图的应用
- 位图的使用
- 位图的定义
- 位图的成员函数
- 位图运算符的使用
- 位图的模拟实现
- 成员函数
- 构造函数
- set reset test
- flip,size,count
- none,any,all
- 位图应用题扩展
- 位图模拟实现代码
位图的介绍
位图的引入
有一道面试题:
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中?
对于这道题,我们有两个思路:
内存内查找: 面对40亿个无符号整数,我们可以使用搜索树和哈希表,时间复杂度也就为O(1),因为搜索树不仅存储数据,还要存储颜色,parent,child指针等,哈希表还要存储迭代器,size等内置成员,进而导致内存存不下.
文件内查找:排序 + 二分查找,时间复杂度为0(1),但是数据太大,只能放在文件上,但是磁盘运行效率太低,不好支持二分查找).
综合以上情况,我们可以采取位图解决:
位图不像搜索树和哈希表那样需要存储数据,数据是否在所给数据中,只有两种状态,在或者不在,那么可以使用一个二进制比特位来代表数据是否存在,二进制比特位为1,代表存在,为0,代表不存在,并且使用直接定址法来确定数据映射位置.
例如以下图示:
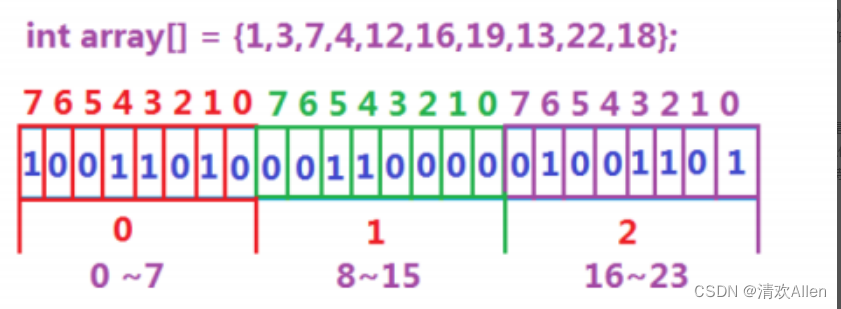
位图的大小判断:
在本题中,40亿的无符号整型的范围为:0–4294967295,在开辟位图空间时,我们不是根据数据的个数在位图上映射的,而是根据数据的大小映射在位图上.所以,我们要开2^32-1的比特位大小的空间,让所有无符号整型数据都能映射在位图上.
那么2^32-1个比特位要占用多少空间呢?
图示如下:

位图的概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,且数据无重复的场景,通常用来判断某个数据存不存在.
位图的应用
1 : 快速查找某个数据打是否在一个集合中.
2: 排序 + 去重 . ( 根据位图性质,哈希函数映射原理)
3: 求两个集合的交集,并集等.
4: 操作系统磁块标记.
位图的使用
位图的定义
方式一: 构造一个8位的位图,所有位默认初始化为0.
bitset<8> bs; //00000000
方式二: 构造一个8位的位图,使用string类型对象初始化.
bitset<8> bs( string("1111" )) // 00001111
方式三: 构造一个8位的位图,使用字符串"1111"初始化.
bit<8> bs("1111"); //00001111
位图的成员函数
| 成员函数 | 作用 |
|---|---|
| set | 设置指定位或所有位(状态设为1 ) |
| reset | 清空指定位或所有位(状态设为0) |
| test | 获取指定位的状态 |
| flip | 反转指定位或者所有位 |
| count | 获取被设置位的个数 |
| size | 获取位图中可以容纳状态位的个数 |
| any | 查看位图所有状态位中是否有1 |
| none | 查看位图中状态位是否都为空 |
| all | 查看位图中状态位是否都为1 |
#include <bitset>
int main()
{
bitset<8> bs("1110");
bs.set(0); //设置指定位
cout << bs << endl; //00001111
bs.reset(0); //清空指定位
cout << bs << endl; //00001110
bs.flip(0); //反转指定位
cout << bs << endl; //00001111
cout << bs.none() << endl; //0
cout << bs.any() << endl; //1
bs.set(); //将位图所有位设置为1
cout << bs.all() << endl; //1
}
注意:
flip,set,reset等成员函数如果未设置指定位时,则默认作用于位图中的全部数据
如果设置指定位,则作用于指定位.
位图运算符的使用
位图中针对运算符进行了重载,我们可以直接在位图中使用.
#include <bitset>
int main()
{
bitset<8> bs; //00000000
//输入运算符
cin >> bs; //1111
//输出运算符
cout << bs << endl; //00001111
bitset<8> bs1("1110");
bitset<8> bs2("1100");
//位运算符
cout << ( bs1 & bs2) << endl; // 0000 1100
cout << ( bs1 | bs2 ) << endl; // 0000 1110
cout << bs1 ^ bs2 ) << endl; // 0000 0010
//[]运算符
bs1[0] = 1;
cout << bs1 << endl; //0000 1111;
return 0;
}
位图的模拟实现
成员函数
构造函数
我们开辟内存时,一般是以char类型(1个字节)开辟的,如果有N个数据,那么就要需要映射到N个比特位.此时计算时开辟空间时有两种情况:
如果 N / 8整除,那么我们直接根据结果开辟字节空间.
如果N / 8 不被整除,那么剩下的数据就没有比特映射了.
综合以上两种情况:
我们采用不过整没整除,我们都比计算值多开辟一个字节空间.
bit_set()
{
_bit.resize(N / 8 + 1);
}
set reset test
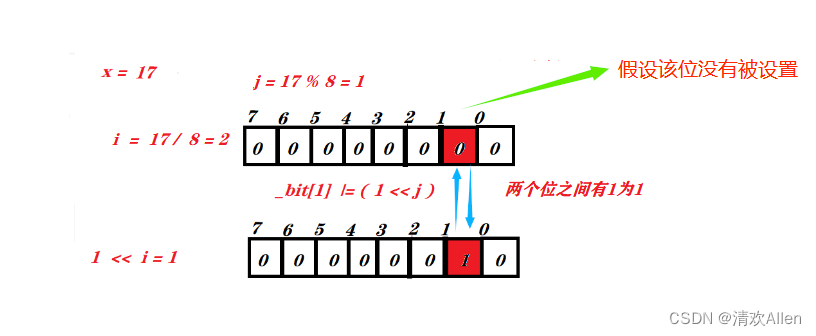
ret成员函数作用主要是将x映射的状态位标为1,
其主要有三个步骤:
(1): 计算数据x在第i个char类型大小的字节空间内.
(2): 计算数据x在第i个char类型空间的第j个位中.
(3); 将1左移j位与第i个char类型进行或等运算.
示图如下:
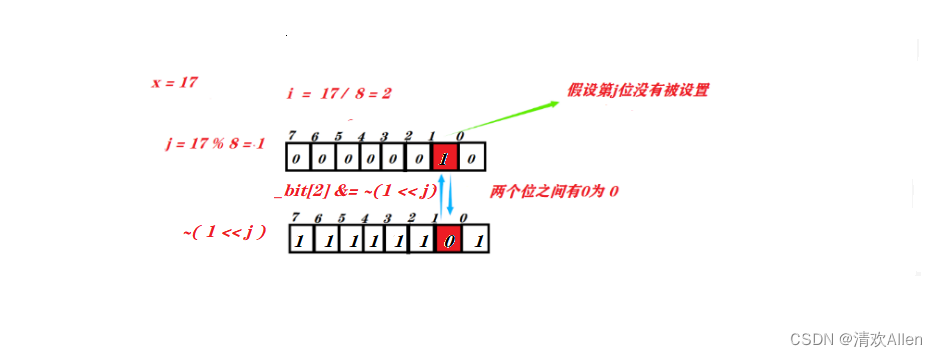
reset成员函数的作用是将x的映射的状态位标为0
其主要有三个步骤:
(1): 计算数据x在第i个char类型大小的字节空间内.
(2): 计算数据x在第i个char类型空间的第j个位中.
(3): 将1左移j位取反后再与第i个类型进行与等运算.
图示如下:
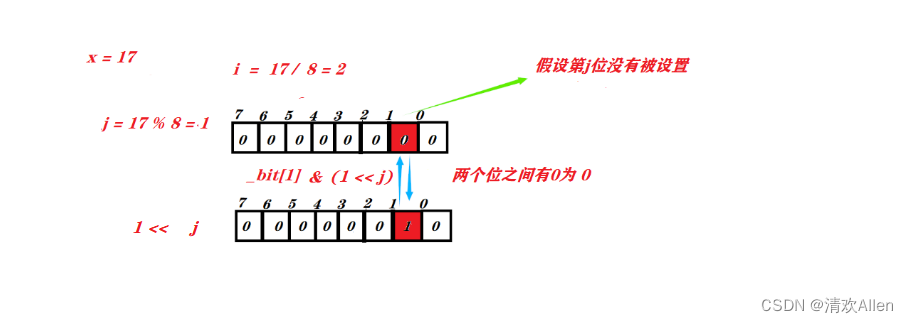
test成员函数的作用是检测x映射的状态位的状态
如果第j位的状态为 0, 那么经过与运算的结果就为0,转换为bool就表示false.
如果第j位的状态位 1, 那么经过与运算的结果为1,转换为bool表示true.
代码如下:
void set(size_t x )
{
size_t i = x / 8;
size_t j = x % 8;
_bit[i] &= ~(1 << j);
}
flip,size,count
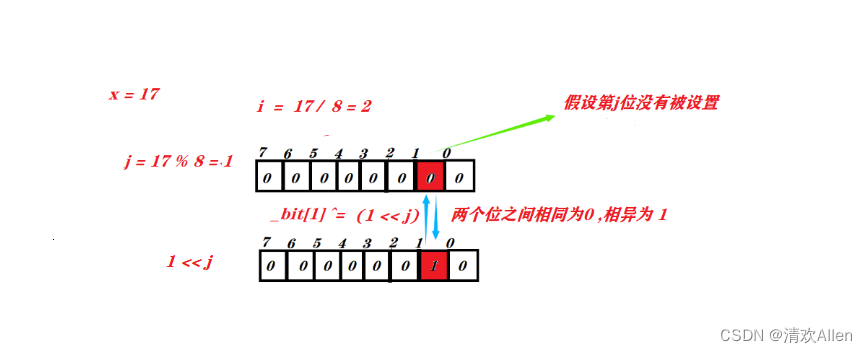
flip成员函数用于反转比特位.
filp成员函数步骤如下:
1: 计算该位位于第i个char类型的第j个比特位.
2: 将1左移j位后再与第i个char类型异或运算.
void flip ( size_t x )
{
size_t i = x / 8;
size_t j = x % 8;
_bit[i] ^= ( 1 << j );
}
size成员函数用于获取位图中可以容纳的位的个数
直接返回非类型模板参数就代表了数据的个数,也就代表了位图的大小.
size_t size()
{
return N;
}
count成员用于获取被设置位的个数
我们知道,获取位图中被设置的位的个数,也就是统计中位图中状态位为1的个数.
步骤如下:
1: 遍历位图,取类型为char大小的比特位n和n-1进行与运算进而得到新的n.(每次计算都使位图状态位为1的个数-1.)
2: 判断n是否为0,如果不为0则继续循环(循环的次数,就代表该char类型比特位为1的个数)
3: 当位图遍历完,每个char类型的比特位循环的总次数就代表了该位图状态为1的总个数.
size_t count()
{
size_t count = 0;
for ( auto e: _bits)
{
char x = e;
while ( x )
{
x = x & (x - 1);
count++;
}
}
return count;
}
none,any,all
none查看位图中是否状态位都为空
在位图中以char类型大小的比特位进行遍历,查看是否为0.
bool none()
{
for ( auto e : _bit )
{
if( e != 0 )
{
return false;
}
}
return true;
}
any函数查看位图中的状态位是否存在1.
bool any()
{
return !none();
}
这里是引用all函数查看位图中的状态位是否都为1.
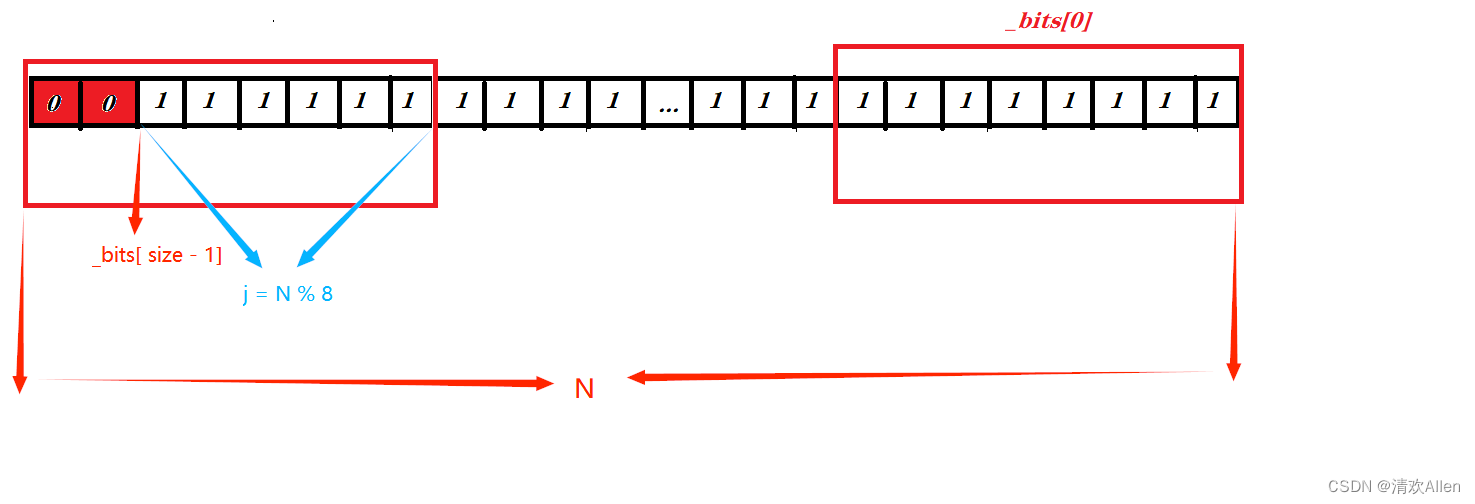
由于我们在构造位图时始终多开了一个char类型大小(8比特位)的空间,且这最后8比特位中只N%8个比特位是有效的,剩下的空间是没有数据映射的,是无效的,此时有两种情况:
步骤如下:
1:检查数据N所占实际的char个数空间大小,即N / 8.
2: 检查最后一个char中有效的比特位是否位1.
bool all()
{
size_t size = _bits.size();
for (size_t i = 0; i < N / 8; i++)
{
if (~_bits[i] != 0)//取反应该为0,否则取反之前不全为1,返回false
return false;
}
for (size_t j = 0; j < N % 8; j++) //再检查最后一个char的前 N%8 个位
{
if ((_bits[ size- 1 ] & (1 << j)) == 0)//最后一个char有多少j个1就循环j次.
return false;
}
return true;
}
位图应用题扩展
题目一:
给定100亿个整数,设计算法找到只出现一次的整数?
我们知道1个位图可以表示两种状态,那么两个位图可以表示四种状态,针对该题,我们可以设计以下三种状态:

为了减少哈希映射位置的计算,我们可以采取复用位图的方式,设计出包含两个位图的类.
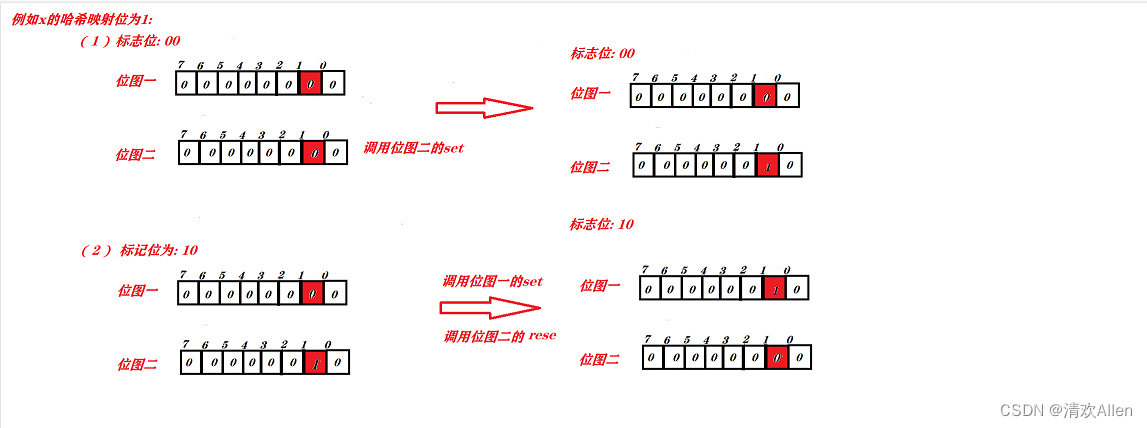
其中成员函数set的作用及步骤如下:
如果x映射位置的状态位为00, 则调用位图2的set,进而实现状态位为01.
如果x映射位置的状态位为01,则调用位图1的set,位图2的reset,进而实现总状态位为10.
图示如下:
代码如下:
template < size_t N >
class twobit_set
{
public:
void set(size_t x)
{
bool inset1 = _bs1.test(x);
bool inset2 = _bs2.test(x);
if ( inset1 == false && inset2 == false ) //如果状态为 00
{
_bs2.set(x); //设计为01;
}
else if (inset1 == false && inset2 == true) //如果状态为 01
{
_bs1.set(x);
_bs2.reset(x); //设计为10
}
}
void print_once_num() //遍历比特位,将数据在位图的状态位为01的数据打印.
{
for ( size_t i = 0; i < N; ++i )
{
if (_bs1.test(i) == false && _bs2.test(i) == true)
{
cout << i << " ";
}
}
}
private:
bit_set<N> _bs1;
bit_set<N> _bs2;
};
代码如下:
题目二:
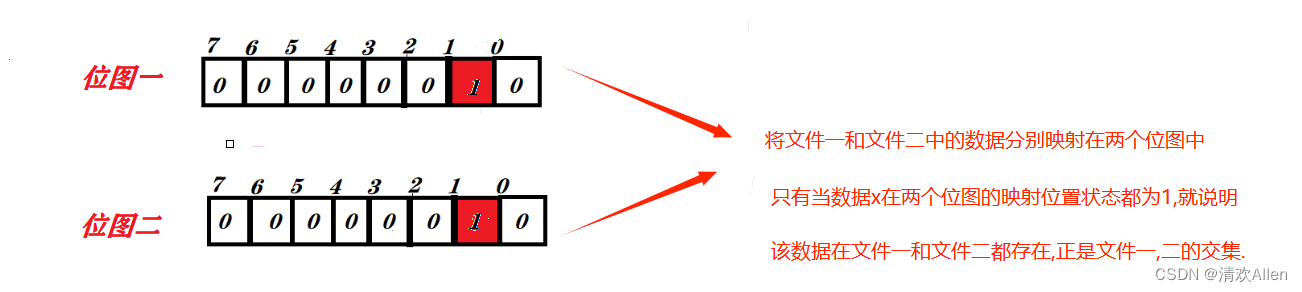
给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件的交集?
题解如下:
template < size_t N >
class twobit_set
{
public:
void set(size_t x) // 00 变 01
{
bool inset1 = _bs1.test(x);
bool inset2 = _bs2.test(x);
if ( inset1 == false && inset2 == false )
{
_bs2.set(x);
}
else if (inset1 == false && inset2 == true) // 01 变 10
{
_bs1.set(x);
_bs2.reset(x);
}
else if (inset1 == true && inset2 == false) // 10 变 11;
{
_bs1.set(x);
_bs2.set(x);
}
}
void print_once_num()
{
for ( size_t i = 0; i < N; ++i )
{
if (_bs1.test(i) == true && _bs2.test(i) == true) //将状态为11的数据打印.
{
cout << i << " ";
}
}
}
private:
bit_set<N> _bs1;
bit_set<N> _bs2;
};
位图模拟实现代码
using namespace std;
namespace myBit
{
template< size_t N >
class bit_set
{
public:
bit_set()
{
_bits.resize(N / 8 + 1, 0);
}
void flip(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
_bits[i] ^= (1 << j);
}
void set(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
_bits[i] |= (1 << j);
}
void reset(size_t x)
{
size_t i = x / 8; //计算在位图的第几个char.
size_t j = x % 8; //计算在char中的第几个位置.
_bits[i] &= ~(1 << j); //只改变第j位的比特位,其他位没有改变.
}
//统计set中1的个数
size_t count()
{
int count = 0;
for (size_t i = 0; i <= N / 8; ++i)
{
char n = _bits[i];
while (n)
{
n = n & (n - 1);
count++;
}
}
return count;
}
// for (auto e : _bits)
// {
// char n = e; //
// while (n)
// {
// n = n & (n - 1);
// count++;
// }
// }
// return count;
//}
size_t size()
{
return N;
}
bool test(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
return _bits[i] & (1 << j);
}
bool all()
{
size_t size = N / 8;
for (size_t i = 0; i < N / 8; i++)
{
if (~_bits[i] != 0)//取反应该为0,否则取反之前不全为1,返回false
return false;
}
//再检查最后一个char的前 N%8 个位
for (size_t j = 0; j < N % 8; j++)
{
if ((_bits[ N - 1 ] & (1 << j)) == 0)//和test的原理一致
return false;
}
return true;
}
bool none()
{
for (auto e : _bits)
{
if (e != 0)
{
return false;
}
}
return true;
}
bool any()
{
return !none();
}
private:
vector<char> _bits;
};
template < size_t N >
class twobit_set
{
public:
void set(size_t x) // 1:00 变 01 2: 01 变 10
{
bool inset1 = _bs1.test(x);
bool inset2 = _bs2.test(x);
if ( inset1 == false && inset2 == false )
{
_bs2.set(x);
}
else if (inset1 == false && inset2 == true)
{
_bs1.set(x);
_bs2.reset(x);
}
else if (inset1 == true && inset2 == false) // 10 变 11;
{
_bs1.set(x);
_bs2.set(x);
}
}
void print_once_num()
{
for ( size_t i = 0; i < N; ++i )
{
if (_bs1.test(i) == false && _bs2.test(i) == true)
{
cout << i << " ";
}
}
}
private:
bit_set<N> _bs1;
bit_set<N> _bs2;
};
void test_set() //测试代码
{
bit_set<9> bit_set;
bit_set.set(0);
bit_set.set(1);
bit_set.set(2);
bit_set.set(3);
bit_set.set(4);
bit_set.set(5);
bit_set.set(6);
bit_set.set(7);
bit_set.set(8);
bit_set.flip(0);
cout << bit_set.none() << endl;
cout << bit_set.count() << endl;
}
}