HF的智能小车车

签到题目，

#include<iostream>

using namespace std;

int main()
{
	string arr;
	cin>>arr;
	if(arr=="R") cout<<"L";
	else if(arr=="L") cout<<"R"<<endl;
	else if(arr=="U") cout<<"D"<<endl;
	else if(arr=="D") cout<<"U"<<endl;
 }

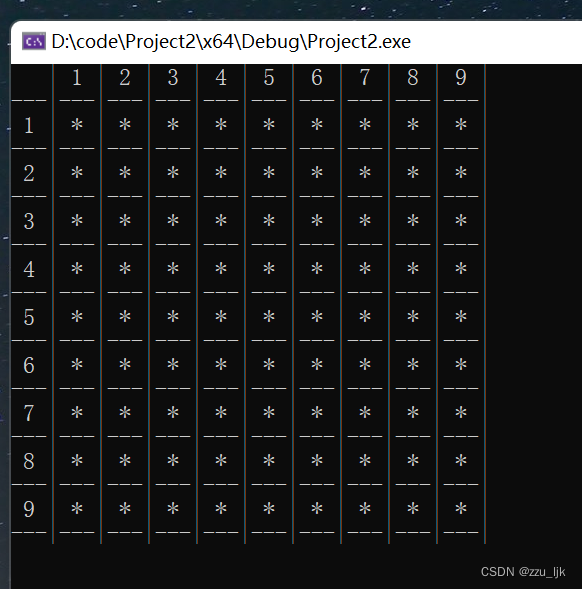
Do you like Van game？

这道题目是个小模拟题目，模拟范围并不大，所以我们可以直接进行模拟。

首先我们发现无非就是三种情况，最开始在1,2,3三个位置，我们可以直接开个变量假设就在初始的三个位置，然后对于每一次的交换，我们都把位置改变，接下来猜一下位置对不对，对了就把对应的答案加一；

代码如下：

#include<iostream>

using namespace std;

int main()
{
	int n;
	cin>>n;
	int a=1,b=2,c=3;//假设abc为初始在123位置 
	int ans1=0,ans2=0,ans3=0;// 记录猜对的次数 
	while(n--)
	{
		int x,y,z;
		cin>>x>>y>>z;
		if(x==a) a=y;
		else if(y==a) a=x;
		
		if(x==b) b=y;
		else if(y==b) b=x;
		
		if(x==c) c=y;
		else if(y==c) c=x;
		//对于每一次交换，如果他交换了，就把他的位置改变 
		if(a==z) ans1++;
		if(b==z) ans2++;
		if(c==z) ans3++;
		//三种初始位置分别计数 
	}
	int ans=max(ans1,ans2);
	ans=max(ans,ans3);//求出最大猜对次数即可，不需要猜位置 
	cout<<ans<<endl;
}

好姐姐的三角形

也是很经典的一道模拟题目，输出经典的三角形，主要需要发现的是外面的空格个数和内层的空格个数，一定要思路清晰，不然空格个数判断错误的话很难改正。

#include<iostream>

using namespace std;

int main()
{
	int n;
	cin>>n;
	while(n--)
	{
		int a;
		char k;
		cin>>a>>k;
		int p=1;
		for(int i=a-1;i>=1;i--)//外层空格数目是逐渐减少，从a-1个开始减少 
		{
			for(int j=1;j<=i;j++) cout<<" ";//这里是外层空格 
			cout<<k;
			if(i!=a-1)//注意，第一层中间没有空格 
			{
				for(int j=1;j<=p;j++) cout<<" ";//如果中间需要空格，进行空格判断，增长规律是p+=2 
				p+=2;
				cout<<k;
			} 
			cout<<endl;
		}
		for(int i=1;i<=2*a-1;i++) cout<<k;//最后一层全是 
		cout<<endl;
		cout<<endl;
	}
 }

帮帮小陈

目前不会写，先放着；

三重循环别想，绝对超时，二分可以优化，但是没想到怎么做；

卷点

这道题目我们需要分类讨论，不难发现，有几个特殊点位需要我们注意

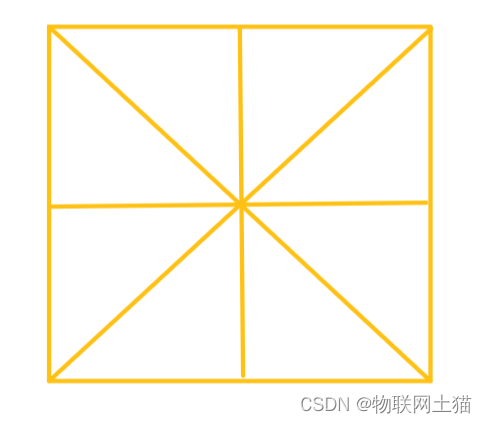
当位于十字和斜线上的时候，我们会发现只有四种情况，可以通过对称实现，而当位于中心点四种情况会重叠，只有一种情况成立，其他情况我们发现都会有八种对称情况，那么根据分析，我们就可以把答案写出来了；

#include<iostream>
#include<set>
using namespace std;
typedef long long LL;
int main()
{
	int n;
	cin>>n;
	while(n--)
	{
		set<LL> se;//这里使用到的是c++STL中的set容器，具体放入set的元素不重复（自动去重） 
		LL a,b,c,d;
		cin>>a>>b>>c>>d;
		se.insert(a);
		se.insert(b);
		se.insert(c);
		se.insert(d);//我们需要特判，这里的面积比其实是高之比 
		
		if(a+b==c+d||a+c==b+d||a+d==b+c)//如果发现有两条边相加相等的情况，说明内部有卷点，如果有卷点，则绝对 
		{                               //存在有两条边相加等于两条边相加，这样三角形高才能和正方形对应 
			if(se.size()==4) cout<<"8"<<endl;//如果发现四条高各不相同，说明不在十字和X上 
			else if(se.size()==2||se.size()==3) cout<<"4"<<endl;//2说明在X上，3说明是在十字上 
			else if(se.size()==1) cout<<"1"<<endl;//四条高相等，只能在中点 
		}
		else cout<<"0"<<endl;//否则高度相加不存在相等的情况肯定无解 
	}
}

/*
补充set：S
<int> 小括号内定义你set可以放入什么类型的数据 
S.insert(A)函数表示把A加入容器。 
s.size()计算s的大小，元素不重复 
s.find(A)！=-1,在set里查找A，不到返回-1 
set的好处就是自动去重，保证每个元素只会出现一次 
*/

签个到就下班

简单题目，签到题

#include<iostream>

using namespace std;

int main()
{
	char a,b;
	string arr;
	cin>>a>>b>>arr;
	int ans=0;
	for(int i=0;i<arr.size();i++)
	{
		if(arr[i]>=a&&arr[i]<=b) cout<<arr[i]<<' ';
	}
}

现在是摸鱼时间

这道题目是一道很搞人的题目。

我们先对式子进行化简，我们可以发现化简到最后得到j-i=arr[j]-arr[i]；说明我们存入数组后，两个位置的下表之差等于他们数组存的数字的差；

那么同学很快就想到了解决方案，我直接暴力循环，只要数组内两个数相减等于下标相减，答案就可以加一，事实上想法没错，但是数据范围在1e6。你是过不去的，会超时，那么我们再想一想，上式还可以化简：j-arr[j]=i-arr[i]也就是说，现在只需要保证下标和数组的差值相等，那么就可以记作一次答案相等；

基于这个思想，我们就可以写出下面这个代码：

#include<iostream>
#include<cstring>
#include<map>
using namespace std;

typedef long long LL;
map<int,int> mp;//这里使用到了map 
int arr[1000010];

int main()
{
    int n;
	LL cnt=0;
	cin>>n;
    
	for(int i=1;i<=n;i++) cin>>arr[i],mp[i-arr[i]]++;//直接计算差值 ，把差值加入到map中 
	for(auto &it:mp)//通过对map差值的遍历，如果出现5次就是10个相等，6个就是15个相等，规律是n个就是1+2+...+n-1 
	{
		int k=it.second;
		for(int i=1;i<k;i++) cnt+=i;//加入我们的答案 
	}
	cout<<cnt<<endl;
	//如果大家不会用map，可以再开一个数组，用这个数组记录差值，差值大小在-999-999之间，数组没负数下标
	//我们可以统一加一个1000，这样范围就在1-1999之间就可以存储，反正我们只要差值的出现次数，不管差值是
	//由谁减谁得到的 
}
/*
map类似字典，根据前一个东西可以定义后一个东西，后一个可以是int类型，也可以是string，甚至可以进行操作；
用法就是直接定义<A,B> A表示字典的第一个关键字，B是字典第二关键字，第二关键字可以进行操作；
具体详细用法请大家去csdn查看； 
*/

现在是摸鱼时间 PLUS

这道题目实际是找两个互质的数字，他们的下标加起来最大是多少，记得不能是1，因为1不是质数不能参与互质运算。

所以很多同学直接暴力，企图循环出1e6的答案，肯定错误，我们发现我们的数据大小在1-1000，但是下标在1-1e6，我们可以想个办法把下标对应到数据上，因为只要数据互质，下标我们只取最大的两个即可，所以我们首先对应下标；

之后对数据进行互质判断，如果互质，直接相加即可，因为我们的第一步已经把下标最大存入这个数，所以直接相加一定是下标最大的相加，这样可以把原本1e6*1e6的算法变为1e3*1e3，可以过掉

#include<iostream>
#include<cstring>
using namespace std;

typedef long long LL;
int arr[1010];

int gcd(int a, int b)
{
    return b>0 ? gcd(b, a % b) : a;
}//判断互质函数，大家也可以写其他判断方法，这个是最简判断 
int main()
{
    int n;
	LL cnt=0;
	cin>>n;
    
	for(int i=1;i<=n;i++) 
	{
		int a;
		cin>>a;
		arr[a]=max(arr[a],i);//将下标对应到数据，且只要最大的 
	}
	int ans=0;
//	for(int i=1;i<=10;i++) cout<<arr[i]<<' ';
	
	for(int i=1;i<=1000;i++)
	{
		for(int j=i;j<=1000;j++)
		{
			if(i==j)//如果天数相同只算1次 
			{
				ans=max(ans,arr[i]);
				if(i==1)//特判样例1 1，因为1 1不是指质数不能进行下面比较，但是1 1的确算作两次摸鱼，所以要特判 
				ans=max(ans,arr[i]*2);
			}
			else if(gcd(i,j)==1&&i!=1&&j!=1)//如果互质，且没有1，就进行摸鱼答案判断 
			{
				ans=max(ans,arr[i]+arr[j]);
			} 
		}
	}
	cout<<ans<<endl;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/470.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！