🎈 作者：Linux猿

🎈 简介：CSDN博客专家🏆，华为云享专家🏆，Linux、C/C++、云计算、物联网、面试、刷题、算法尽管咨询我，关注我，有问题私聊！

🎈 关注专栏： 数据结构和算法成神路【精讲】优质好文持续更新中……🚀🚀🚀

🎈 欢迎小伙伴们点赞👍、收藏⭐、留言💬

一、什么是最小生成树？

二、克鲁斯卡尔（Kruskal）算法

2.1 Kruskal 算法起源

2.2 算法原理

2.3 实例演示

2.4 算法模板

2.5 算法复杂度

2.5.1 时间复杂度

2.5.2 空间复杂度

三、真题练习

四、总结

这篇文章来讲解下图论算法之「克鲁斯卡尔（Kruskal）」，「克鲁斯卡尔（Kruskal）」通常用于求解最小生成树，求解最小生成树的算法还有「普里姆（Prim）」算法和「Boruvka」算法，下面就来看下「克鲁斯卡尔（Kruskal）」算法吧！

🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶

一、什么是最小生成树？

在介绍具体算法之前，先来说下什么是「最小生成树」？

假设在 n 个城市之间铺设网络，使得 n 个城市能够互相通信，已知任意两个城市之间铺设网络的费用，如何使得费用最小？

很显然，只需要铺设 n - 1 条线路即可使得 n 个城市能够互相通信。（n 个点构成一个连通图至少需要 n - 1 条边）。

「最小生成树」是指构造连通网的最小代价生成树，所以最小生成树具有 n 个顶点 n - 1 条边。

构造一个连通网的最小生成树通常有三大算法：「普里姆（Prim）」算法、「克鲁斯卡尔（Kruskal）」以及「Boruvka」算法。

本篇文章来介绍一下「克鲁斯卡尔（Kruskal）」算法，「普里姆（Prim）」算法已经在上一篇文章中讲解过文章链接。

🔶🔶🔶🔶🔶 我是华丽的分割线 🔶🔶🔶🔶🔶

二、克鲁斯卡尔（Kruskal）算法

2.1 Kruskal 算法起源

克鲁斯卡尔是美国人（数学家、统计员、电脑科学家和心理测量师）。1956年，克鲁斯卡尔提出了 Kruskal 算法，它是一个「贪心算法」，主要用于求解「最小生成树」。

2.2 算法原理

假设图为 G，顶点集合为 V，边的集合为 E，按照「克鲁斯卡尔（Kruskal）」算法求解「最小生成树」的步骤如下所示：

（1）首先，建立新图 G1，G1 的顶点集合为 V1，V1等于原图 G 顶点集合 V，边的集合设为 E1，E1 = {}，集合为空；

（2）将原图 G 中所有的边按权值从小到大排序；

（3）从排序后的权值中从小到大依次选择，选择当前排序后权值最小的边（u, v），如果边（u，v）的两个顶点在新图 G1 中连接两个不同的「连通分量」，则将这条边添加到新图 G1 边的集合 E1 中；

（4）重复步骤（3），直到原图 G 中的所有边都选择完，或者新图 G1 中的所有顶点都在同一个「连通分量」中。

2.3 实例演示

下面通过一个实例演示进行说明，假设无向「图G」如下所示。

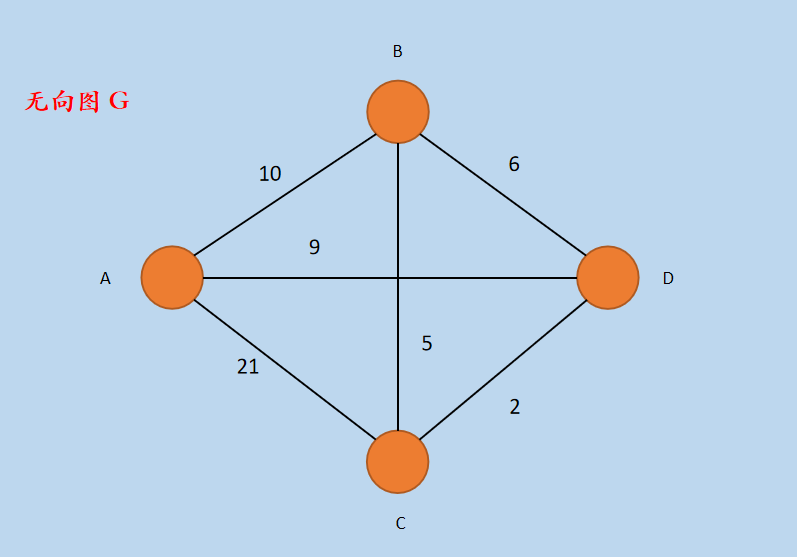
在上图中，包括四个顶点 A、B、C、D 以及相互连接的边，各个边上的数字表示边的权重，上面是一个无向图。

其中，V = {A, B, C, D}, E = {AB, AC, AD, BC, BD, CD}。

（1）初始时 V1 = {A, B, C, D}，E1 = {}，建立新图G1 如下所示。

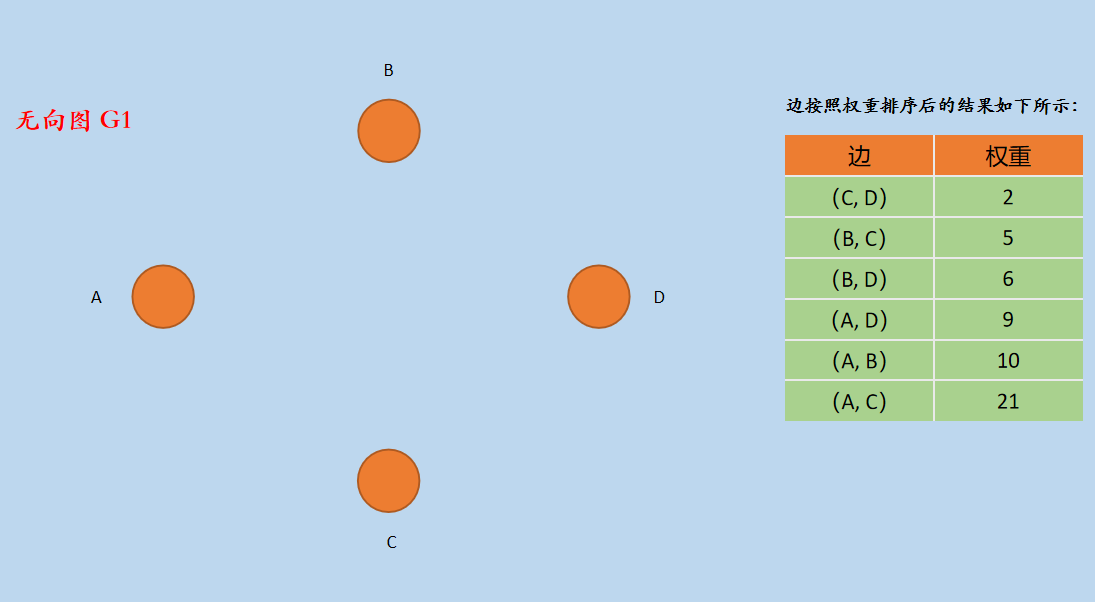
在经过初始化后，无向图 G1 中已经包含原图 G 所有顶点，但是，边的集合 E1 为空，即：V1 = {A，B, C, D}，E1 = {}。

并将原图 G 的边按照权重从小到大排序，如上图中所示。

（2）从排序后的边从小到大开始选择，选择边（C, D），因为 C 和 D 两个顶点在新图 G1 中属于不同的「连通分量」，所以加入到新图 G1 中，加入后图 G1 如下所示：

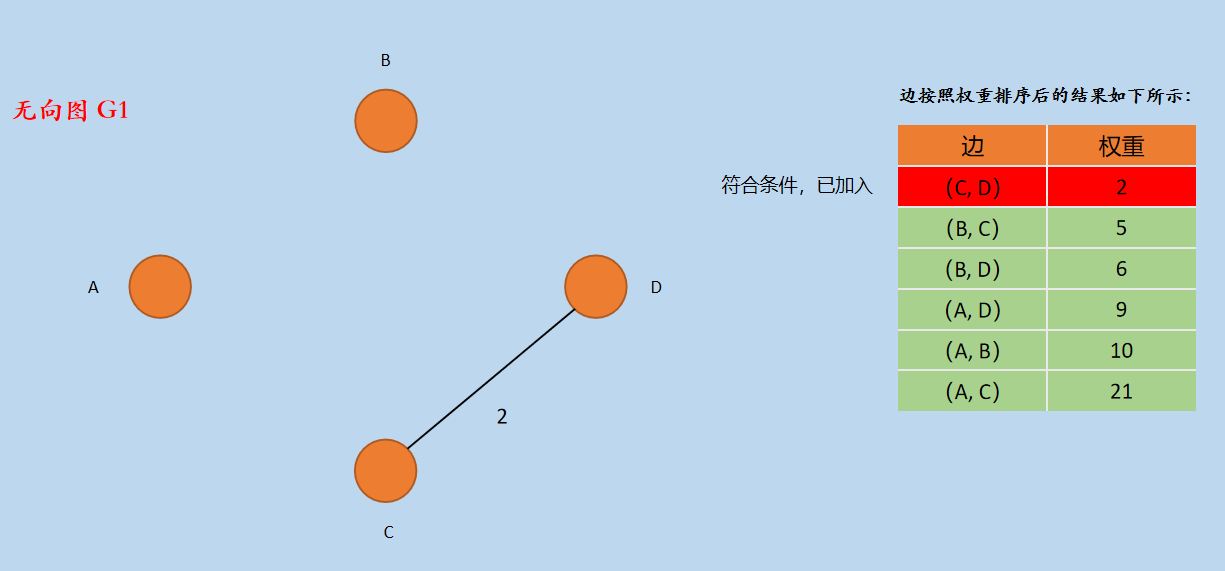
新图 G1的边的集合 E1 = { CD }

（3）按照排序后边的大小，选择边（B, C），因为顶点 B 和顶点 C 属于不同的「连通分量」，所以将（B，C）加入到无向图G1中，如下所示：

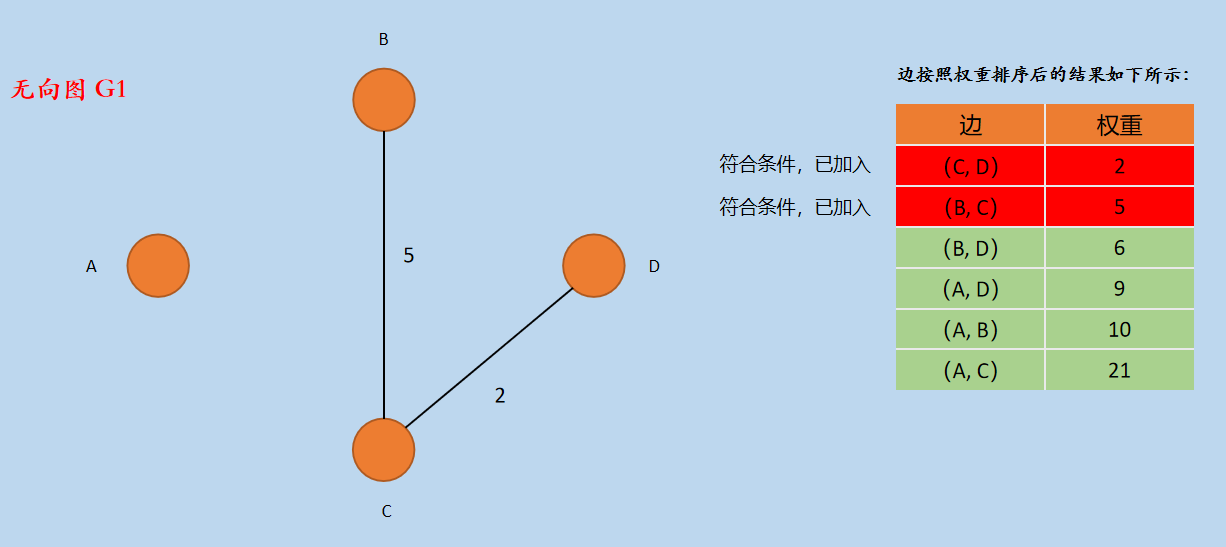
新图 G1 的边的集合 E1 = { CD，BC }。

（4）按照排序后边的权重大小，选择边（B, D），因为顶点 B 和顶点 D 属于相同的「连通分量」，所以（B，D）不能加入到无向图 G1 中。

（5）按照排序后边的权重大小，选择边（A, D），因为顶点 A 和顶点 D 属于不同的「连通分量」，所以将（A，D）加入到无向图 G1 中，如下所示：

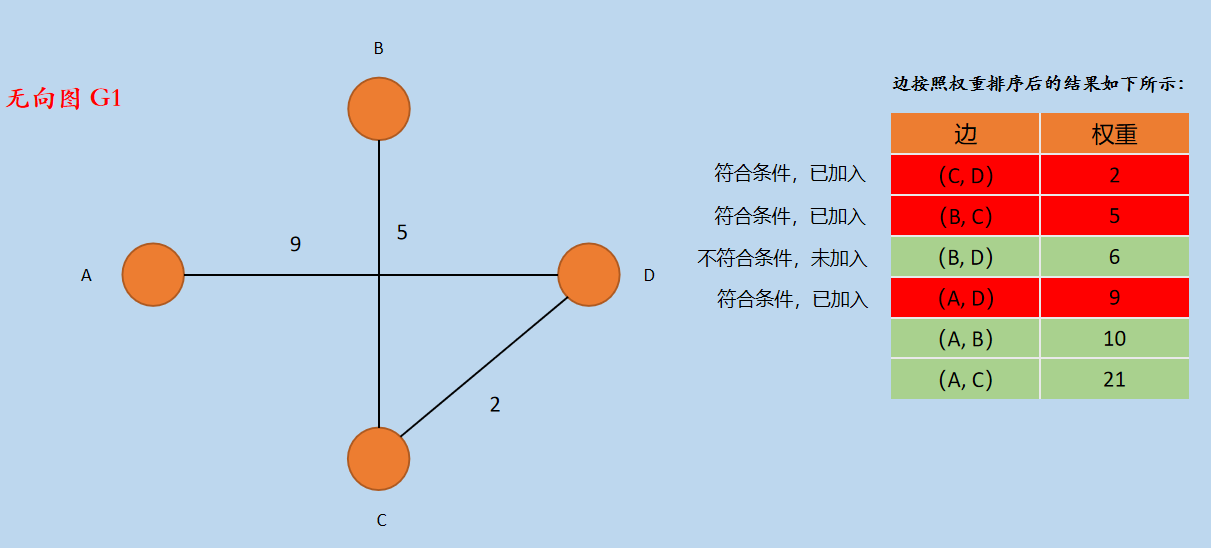
新图G1 的边的集合 E1 = { CD，BC，AD }。

（6）加入边（A, D）后，已经形成了一棵最小生成树，通过 n - 1 条边，连接了 n 个顶点，可以发现剩余的两条边（A，B）和（A, C）如果尝试加入，顶点 A 和顶点 B 属于相同的「连通分量」，顶点 A 和顶点 C 属于相同的「连通分量」，所以都不能加入到图 G1 中。

2.4 算法模板

下面是「克鲁斯卡尔（Kruskal）」算法的算法模板，通过「并查集」查看每次加入边的两个顶点是否为同一个「连通分量」，通过 sort 算法按照权重从小到大排序。

#include<iostream>
#include<algorithm>
using namespace std;
const int SIZE = 1e5 + 5;

int n, m; // n 表示顶点的个数，m 表示边的个数
int father[SIZE];   //记录节点的父节点
// 存储图的边
struct Edge
{
    int u; // 边的顶点
    int v; // 边的顶点
    int w; // 边的权重
}T[SIZE];

/**
 * 通过并查集查找父节点
 */
int find(int u)
{
    if (father[u] != u) {
        father[u] = find(father[u]);
    }
    return father[u];
}

/**
 * 通过 kruskal 计算最小生成树
 * 返回最小生成树的权值和
 */
int kruskal()
{
    //初始化并查集
    for (int i = 1; i <= n; i++)
        father[i] = i;

    //按照边的权值大小排序，使用了 lambda 表达式
    sort(T, T + m, [](const Edge& a, const Edge& b){ return a.w < b.w;});

    //按照权值从小到大选择
    int x, y;
    int num = 0; // 用于统计加入边的个数，可以提前结束下面的 for 循环
    int ans = 0;
    for (int i = 0; i < m; ++i) {
        x = find(T[i].u);
        y = find(T[i].v);
        if (x != y) { // 说明不是一个连通分量
            father[x] = y;
            ans += T[i].w;
            num++;
        }
        if(num == n - 1) break; // 表示新图 G1 中已经有 n - 1 条边，构成了最小生成树
    }
    return num == n - 1 ? ans : -1;
}

/**
 * 获取输入
 * n 表示顶点个数
 * m 表示边的个数
 */
void input() {
    cin>>n>>m;
    //输入 m 条边，其中，u 和 v表示顶点，w 表示边（u, v）的权重
    for(int i = 0; i < m; ++i) {
        cin>>T[i].u>>T[i].v>>T[i].w;
    }
}

/**
 测试数据：
 4 6
 1 2 10
 1 3 21
 1 4 9
 2 3 5
 2 4 6
 3 4 2
 输出结果：16
 选中的边为：(3, 4)、(2, 3)、(1, 4)
**/

int main()
{
    input();
    cout<<kruskal()<<endl;
    return 0;
}

2.5 算法复杂度

2.5.1 时间复杂度

时间复杂度为：O(mlogm)

在上述代码中，耗费时间的操作主要有for 循环初始化 father 数组、sort 排序以及对 m 条边进行 for 循环遍历，时间复杂度分别为：O(n)（for循环 n 时间复杂度）O(mlogm)（快排时间复杂度），O(m)（for 循环 m 时间复杂度），因为这三个时间是串行的，一般取大者为算法的时间复杂度，所以时间复杂度为O(mlogm)。