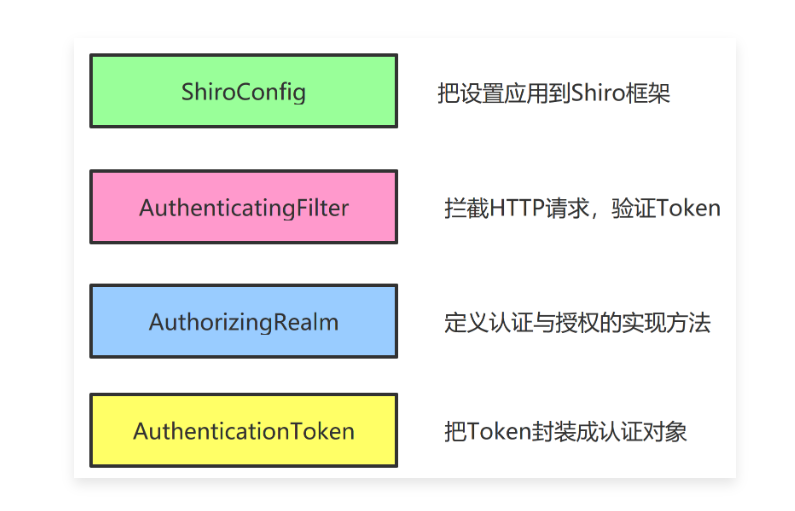
Typora中的数学公式(MarkDown)
添加数学公式方式:
1.选择:段落=>公式
2.快捷键:Ctrl +Shift +M
3.直接输入两个美元符号并回车
展示:
空格:一个斜线\ : a \ b
a
b
a \ b
a b
换行:两个斜线 \ : a \\ b
a
b
a \\ b
ab
分数相乘: \frac{a}{b} \times \frac{c}{d}
a
b
×
c
d
\frac{a}{b} \times \frac{c}{d}
ba×dc
开根号: \sqrt{x} \times \sqrt[n]{y}
x
×
y
n
\sqrt{x} \times \sqrt[n]{y}
x×ny
上标和下标: x^n+ y_3
x
n
+
y
3
x^n+ y_3
xn+y3
向量: \vec{a} \cdot \vec{b} = 0
a
⃗
⋅
b
⃗
=
0
\vec{a} \cdot \vec{b} = 0
a⋅b=0
上划线: \overline{x}
x
‾
\overline{x}
x
极限: \lim_{n\to\infty}n \lim{n}
lim
n
→
∞
n
或
lim
n
\lim_{n\to\infty}n \ 或 \ \lim{n}
n→∞limn 或 limn
积分: \int_0^n f(x)dx \int f(x)dx
∫
0
n
f
(
x
)
d
x
或
∫
f
(
x
)
d
x
\int_0^n f(x)dx \ 或 \ \int f(x)dx
∫0nf(x)dx 或 ∫f(x)dx
求和: \sum_{i=1}^n a_i \sum a_i
∑
i
=
1
n
a
i
或
∑
a
i
\sum_{i=1}^n a_i \ 或 \ \sum a_i
i=1∑nai 或 ∑ai
矩阵:
\bbegin{bmatrix} a&b&c d&e&f \end{bmatrix} \tag{1}
\bbegin{matrix} a&b&c d&e&f \end{matrix} \tag{2}
[
a
b
c
d
e
f
]
(1)
\begin{bmatrix} a&b&c \\ d&e&f \end{bmatrix} \tag{1}
[adbecf](1)
a b c d e f (2) \begin{matrix} a&b&c \\ d&e&f \end{matrix} \tag{2} adbecf(2)
常用数学符号: \cdot \times \div \approx \pm \leq \geq \gt \lt
⋅
×
÷
≈
±
≤
≥
>
<
\cdot \ \times \ \ \div \ \approx \ \pm \ \leq \ \geq \ \gt \ \lt
⋅ × ÷ ≈ ± ≤ ≥ > <
常用逻辑判断符号: \forall \infty \emptyset \exist \nabla \angle \because \therefore
∀
∞
∅
∃
∇
∠
∵
∴
\forall \ \infty \ \emptyset \ \exist \ \nabla \ \angle \ \because \ \therefore
∀ ∞ ∅ ∃ ∇ ∠ ∵ ∴
常用希腊符号: