论文解读者：陈宇文，胡明杰，史铭伟，赵田田

许多实际问题都可以建模为凸优化问题。相比于直接求解原问题，将问题转化为鞍点问题往往会带来好处。求解鞍点问题的一种常用算法是原对偶混合梯度算法 (PDHG)，它在各类问题问题当中均得到了广泛应用。然而，实际应用中遇到的大规模问题会面临较高的计算成本。本文[1]针对对偶变量可分离的鞍点问题提出了PDHG的随机扩展 (SPDHG)。在迭代过程中，可以通过不断积累来自以前迭代的信息来减小方差，进而减少随机性的负面影响。本文分析了一般的凸凹鞍点问题 (convex-concave saddle point problems) 和部分光滑/强凸或完全光滑/强凸问题。本文对任意采样 (arbitrary samplings) 的对偶变量进行分析，并获得已知的确定性结果作为特殊情况。在实验中，本文的多种随机方法在各种成像任务上显著优于确定性变体。

第一部分：问题模型和PDHG算法

1.1 问题形式

设$\mathbb{X}$和${\mathbb{Y}}_i(i=1,\dots ,n)$是实希尔伯特空间，并定义$\mathbb{Y}:={\prod }_{i=1}^n{\mathbb{Y}}_i$。此时我们可以根据${\mathbb{Y}}_i$的维数，将$y\in \mathbb{Y}$对应写作$y=\left(y_1,y_2,\dots ,y_n\right)$。设 f : Y → R ∞ : = R ∪ { + ∞ } f: \mathbb{Y} \rightarrow \mathbb{R}_{\infty}:=\mathbb{R} \cup\{+\infty\} f:Y→R∞​:=R∪{+∞}和$g:\mathbb{X}\to {\mathbb{R}}_{\infty }$是凸函数，且$f$是可分的，可写作$f(y)={\sum }_{i=1}^n{f}_i\left(y_i\right)$。设$\mathbf{A}:\mathbb{X}\to \mathbb{Y}$是有界线性算子，$\mathbf{A}x=({\mathbf{A}}_{1}x,\cdots ,{\mathbf{A}}_{n}x)$。问题可写为
$$\underset{x\in \mathbb{X}}{\min }\left\{\Phi (x):=\sum _{i=1}^n{f}_i\left({\mathbf{A}}_{i}x\right)+g(x)\right\}.$$
如果$f$满足适当的条件，则它相当于求解鞍点问题
$$\underset{x\in \mathbb{X}}{\min }\underset{y\in \mathbb{Y}}{\sup }\left\{\Psi (x,y):=\sum _{i=1}^n⟨{\mathbf{A}}_{i}x,y_i⟩-f_i^{\ast }\left(y_i\right)+g(x)\right\},$$
其中$f_i^{\ast }$是$f_i$的Fenchel共轭函数，而$f^{\ast }(y)={\sum }_{i=1}^n{f}_i^{\ast }\left(y_i\right)$是$f$的共轭函数。设$\mathbb{W}:=\mathbb{X}\times \mathbb{Y}$，我们假设上述问题有最优解$w^{\sharp}\in\mathbb{W} $，并将其写作$w^{{\sharp}=\left(x}{\sharp}, y^{{\sharp}\right)=\left(x}{\sharp}, y_1^{\sharp}, \ldots, y_n^{{\sharp}\right)$。鞍点$w}{\sharp}$满足最优性条件
$${\mathbf{A}}_i{x}^{♯}\in \partial f_i^{\ast }\left(y_i^{♯}\right),i=1,\dots ,n,-{\mathbf{A}}^{\ast }{y}^{♯}\in \partial g\left(x^{♯}\right).$$

1.2 PDHG算法

对于正常数$\tau$，可定义$\mathbb{W}$上的带权范数$\Vert x{\Vert }_{{\tau }^{-1}}^2=⟨{\tau }^{-1}x,x⟩$。由此可给出邻近点算子的定义
$${\mathrm{prox}}_f^{\tau }(y):=\arg \underset{x\in \mathbb{X}}{\min }\left\{\frac{1}{2}\Vert x-y{\Vert }_{{\tau }^{-1}}^2+f(x)\right\}$$
类似地，我们可将$\tau$换成对称正定的矩阵。则PDHG算法可写作
$$\begin{array}{rl}& x^{(k+1)}={\mathrm{prox}}_g^{\mathbf{T}}\left(x^{(k)}-{\mathbf{TA}}^{\ast }{\bar{y}}^{(k)}\right),\\ & y_i^{(k+1)}={\mathrm{prox}}_{f_i^{\ast }}^{{\mathbf{S}}_i}\left(y_i^{(k)}+{\mathbf{S}}_i{\mathbf{A}}_i{x}^{(k+1)}\right),i=1,\dots ,n,\\ & {\bar{y}}^{(k+1)}=y^{(k+1)}+\theta \left(y^{(k+1)}-y^{(k)}\right),\end{array}$$

其中$\mathbf{S}=\mathrm{diag}\left({\mathbf{S}}_1,\dots ,{\mathbf{S}}_n\right)$，${\mathbf{S}}_1,\dots ,{\mathbf{S}}_n$和$\mathbf{T}$都是对称正定的矩阵。

第二部分：Stochastic PDHG

2.1 随机PDHG算法

在PDHG算法中，每一次迭代都需要更新所有$y_i(i=1,\cdots ,n)$的值。我们现在考虑每次抽取 { 1 , ⋯   , n } \{1,\cdots,n\} {1,⋯,n}的一个子集$\mathbb{S}$，然后只更新满足$i\in \mathbb{S}$的$y_i$。其中$\mathbb{S}$的选取满足：对于每次迭代，任意的指标$i$都以$p_i>0$的概率被包含在$\mathbb{S}$中（这样的条件不难满足，常见的选取方式包括：全采样，即$\mathbb{S}$以1的概率取到 { 1 , ⋯   , n } \{1,\cdots,n\} {1,⋯,n}; 连续采样，即$\mathbb{S}$以$p_i$的概率取到 { i } \{i\} {i}）。设$\mathbf{Q}:=\mathrm{diag}\left(p_1^{-1}\mathbf{I},\dots ,p_n^{-1}\mathbf{I}\right)$，则随机PDHG算法可写作

可以看出，SPDHG与PDHG的不同点在于$y_i^{k+1},{\bar{y}}^{k+1}$的更新。SPDHG采用降采样对部分$y_i^{k+1}$进行更新，同时${\bar{y}}^{k+1}$的更新需要乘上新的系数矩阵$\mathbf{Q}$。

2.2 ESO条件

在随机PDHG算法的收敛性分析中，经常用到ESO条件。$\mathbb{S}$和$p_i(i=1,\cdots ,n)$如上文定义。设$\mathbf{C}:\mathbb{X}\to \mathbb{Y}$是有界线性算子，$\mathbf{C}x=({\mathbf{C}}_{1}x,\cdots ,{\mathbf{C}}_{n}x)$。我们说 { v i } ⊂ R n \left\{v_i\right\} \subset \mathbb{R}^n {vi​}⊂Rn满足ESO条件，当且仅当对任意$z\in \mathbb{Y}$有
$${\mathbb{E}}_{\mathbb{S}}{\Vert \sum _{i\in \mathbb{S}}{\mathbf{C}}_i^{\ast }{z}_i\Vert }^2\le \sum _{i=1}^n{p}_i{v}_i{\Vert z_i\Vert }^2.$$

这样的条件也不难满足。对于全采样，我们可取${\mathbf{C}}_i={\mathbf{S}}_i^{1/2}{\mathbf{A}}_i{\mathbf{T}}^{1/2}$和$v_i=\Vert \mathbf{C}{\Vert }^2$；对于连续采样，我们可以取相同的${\mathbf{C}}_i$以及$v_i={\Vert {\mathbf{C}}_i\Vert }^2$。

2.3 收敛速度

在考虑SPDHG收敛性之前，我们首先简单介绍一下Bregman距离$D_h(w,v)$和对偶间隙$G(x,y)$(duality gap)。

1）Bregman距离$D_h(w,v)$的作用与范数 (norm) 类似：

$$\begin{array}{c}{D}_h(w,v):=h(w)-h(v)-⟨\nabla h(v),w-v⟩.\end{array}$$

如果选取$h(w)=\Vert w{\Vert }^2$，那么此时有$D_h(w,v)=\Vert w-v{\Vert }^2$，也就是2-范数。其中，对于本文的minimax问题，作者定义$w:=(x,y)$，并选取$h(w):=g(x)+{\sum }_{i=1}^n{f}^{\ast }(y_i)$。

2）与此同时，对偶间隙$G(x,y)$通常可用来进行收敛性分析，定义如下

$$\begin{array}{c}{G}_{{\mathbb{B}}_1\times {\mathbb{B}}_2}(x,y):=\underset{\tilde{y}\in {\mathbb{B}}_2}{\sup }\Psi (x,\tilde{y})-\underset{\tilde{x}\in {\mathbb{B}}_1}{\inf }\Psi (\tilde{x},y).\end{array}$$

minmax问题最优解$(x^{\ast },y^{\ast })$满足对偶间隙$G(x^{\ast },y^{\ast })=0$。

对于收敛速度，文章中考虑了对应一般凸 (convex)，半强凸 (semi-strongly convex) 和强凸 (strongly convex) 三类情况下Bregman距离$D_h(w^k,w^{\ast })$与对偶间隙$G(w)$的收敛速度。

一般凸问题

此时Bregman距离$D_h(w^k,w^{\ast })$与对偶间隙$G(w)$的收敛速度为$O\left(\frac{1}{K}\right)$(见文中定理4.3)。需要注意的是，此时Bregman距离中$h(w)$不是强凸，它的收敛性质和通常我们理解的范数是有区别的！！！ (感兴趣的同学可以参考原论文中的Remark 4)

半强凸问题

半强凸问题被定义成$g(x)$或者$f_i^{\ast }(y)$中存在其中一个是强凸的。文章中假设$f_i^{\ast }(y)$是强凸的 ($g(x)$一般凸)，那么对偶空间中的Bregman距离性质就会和正常的范数一致，对偶序列 { y k } \{y^k\} {yk}最终能收敛到对偶最优解$y^{\ast }$。同时，当我们采用自适应的缩放矩阵 (adaptive scaling)，那么序列速度将改进为$O\left(\frac{1}{K^2}\right)$(见文中定理5.1)。改进后的Algorithm 3如下所示：

同理，如果假设$g(x)$是强凸的 ($f_i^{\ast }(y)$一般凸)，那么原始空间中的Bregman距离性质就会和正常的范数一致，原始序列 { x k } \{x^k\} {xk}最终能收敛到对偶最优解$x^{\ast }$。并且在论文中Algorithm 2下，序列速度将改进为$O\left(\frac{1}{K^2}\right)$。

强凸问题

如果问题中$g(x)$和$f_i^{\ast }(y)$都是强凸的，那么原始空间和对偶空间中的Bregman距离性质都会和正常的范数一致，序列$\{(x^k,y^k)\}$最终能收敛到对偶最优解$(x^{\ast },y^{\ast })$。并且对于Algorithm 1，序列$\{(x^k,y^k)\}$将以线性速度收敛 (见文中定理6.1)。

另外的证明思路：​

值得一提的是，最近研究人员又发现了另外一种基于随机算子理论 (stochastic operator) 来分析SPDHG收敛速度的方法。感兴趣的同学可以阅读这篇论文[2]。

第三部分：数值实验

本章有四个例子关于total variation，我们选取Huber-TV deblurring (对应Sec 7.3的Algorithm 3实验) 展开说明，剩下的三个例子原理类似。我们首先介绍一下TV operator的基本概念，方便读者理解。

对于$x\in {\mathbb{R}}^{d_1\times d_2}$，TV算子定义如下：

$${\mathcal{R}}_{V^{\beta }}(\mathbf{x})=\sum _{i,j}{\left({\left(x_{i,j+1}-x_{ij}\right)}^2+{\left(x_{i+1,j}-x_{ij}\right)}^2\right)}^{\frac{\beta }{2}}.$$

上述方程的意思是: 计算每一个像素和横向下一个像素的差的平方，加上纵向下一个像素的差的平方; 然后开$\beta /2$次根。在这个例子中，我们考虑一个去模糊的卷积核，它有前向操作符${\mathbf{A}}_1$类似于执行卷积 用一个移动的卷积核15*15像素的在长408，宽544像素的图片上。图片中的噪声用泊松方法在恒定的200像素的背景下，去估计数据的均值694.3。我们进一步假设有知道重建的图像应该是非负的和有上限的100倍。根据正向运算符的性质，只要$x\ge 0,\mathbf{A}x\ge 0$。此时对偶问题下新的KL散度是

$$f_i^{\ast }(z)=\sum _{i=1}^N\{\begin{array}{ll}\frac{r_i^2}{2b_i}{z}_i^2+\left(r_i-\frac{r_i^2}{b_i}\right)z_i+\frac{r_i^2}{2b_i}+\frac{3b_i}{2}-2r_i-b_i\log \left(\frac{b_i}{r_i}\right),& \text{ if }{z}_i<1-\frac{b_i}{r_i},\\ -r_i{z}_i-b_i\log \left(1-z_i\right),& \text{ if }1-\frac{b_i}{r_i}\le z_i<1,\\ \infty ,& \text{ if }{z}_i\ge 1.\end{array}$$

之后，我们可以进行实验前的参数设计。在这个实验中，我们选择$\gamma =0.99$考虑均匀采样，即$p_i=1/n$。在确定性情况下，子集的数量为$n=1$或者在随机情况下$n=3$。初始步长参数被选择为

PDHG: ${\sigma }_i=\tau =\gamma /\Vert \mathbf{A}\Vert \approx 0.095$;
DA-PDHG:${\tilde{\sigma }}_i^{(0)}={\mu }_f/\Vert \mathbf{A}\Vert \approx 0.096,{\tau }^{(0)}=\gamma /\Vert \mathbf{A}\Vert \approx 0.095$;
DA-SPDHG:${\tilde{\sigma }}^{(0)}={\min }_i\frac{{\mu }_i{p}_i^2}{{\tau }^0{\Vert {\mathbf{A}}_i\Vert }^2+2{\mu }_i{p}_i\left(1-p_i\right)}\approx 0.073$,${\tau }^{(0)}=1/\left(n{\max }_i\Vert {\mathbf{A}}_i\Vert \right)\approx 0.032$

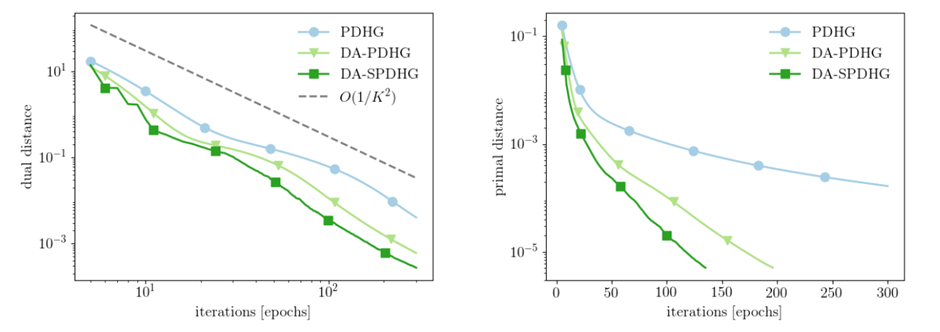
图1 Huber-TV 去模糊双加速 (左图是对偶变量$y$，右图为原始变量$x$)

图1的定量结果表明算法收敛确实有$O\left(\frac{1}{K^2}\right)$的比率，如定理 5.1 所证明的。此外，他们还表明随机化和加速可以结合使用以进一步加速。

在另外一篇论文中[3], 采用确定性PDHG的2000次迭代结果（近似）作为视觉和定量比较的鞍点。我们首先看从 3 中 100 次预期算子评估后的重建图像可以看出，SPDHG比确定性PDHG快得多 (下图2)。虽然使用 PDHG 的重建仍然存在伪影，但使用 SPDHG 重建的图像在 100 次迭代后在视觉上与鞍点非常相似。

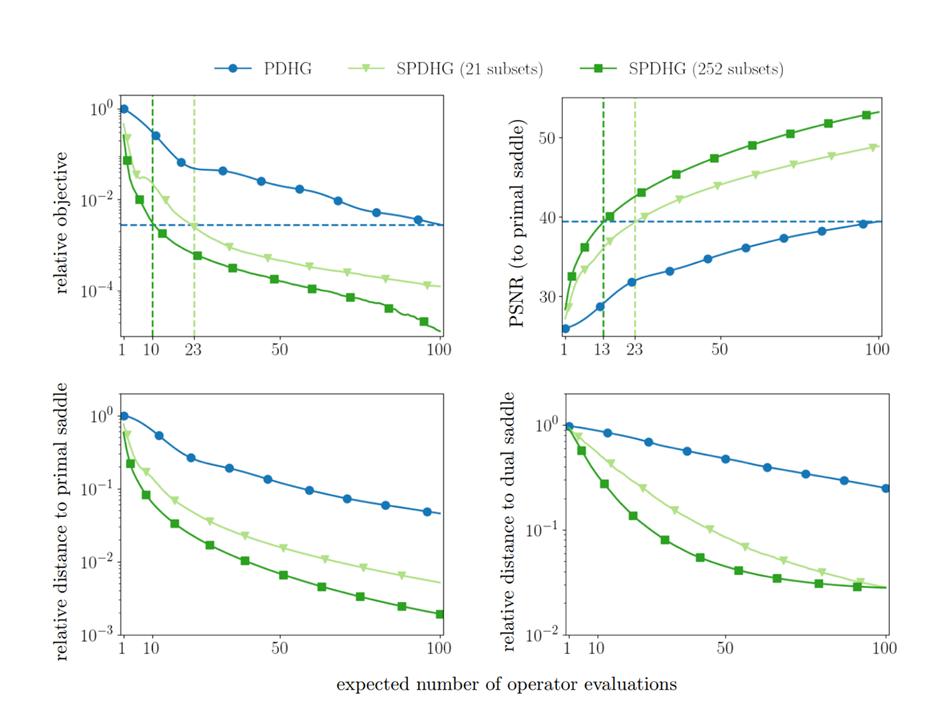
图2. 不同子集SPDGH 和PDGH比较 (横轴是不同数量操作符评估，纵轴是主要鞍点的相对距离)

另外，从图3中看，具有21和252个子集的SPDHG与仅经过 20 次预期操作员评估后的PDHG的比较。PDHG的结果在临床上无用，因为主要的解剖结构尚不可见。 另一方面，随着越来越多的子集，即使付出一点点努力，也可以重建一个合理的 (虽然不完美) 图像。与之相对的SPDHG，随着将像素点分割成越来越多的子集，即使付出⼀点点努力，也可以重建⼀个合理的 (虽然不完美) 图像 (如图3所示)。同时，还很容易看出，随着⼦集越多，伪影越少，这表明随着⼦集越多，算法收敛得越快。

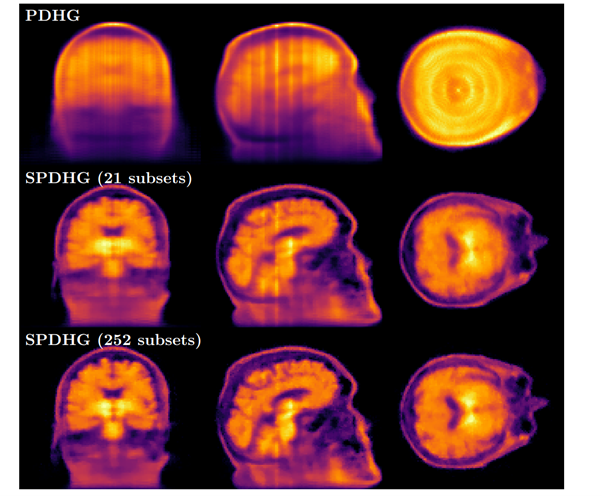
图3: TV先验PET重建, 20个迭代周期下的结果

参考文献：

[1] Chambolle, Ehrhardt, Richtárik & Schönlieb (2018). Stochastic Primal-Dual Hybrid Gradient Algorithm with Arbitrary Sampling and Imaging Applications. SIAM Journal on Optimization, 28(4), 2783–2808.

[2] Ahmet Alacaoglu, Olivier Fercoq, and Volkan Cevher (2022). On the Convergence of Stochastic Primal-Dual Hybrid Gradient. SIAM Journal on Optimization, 32(2), 1288-1318.

[3] Ehrhardt, Matthias & Markiewicz, Pawel & Richtárik, Peter & Schott, Jonathan & Chambolle, Antonin & Schönlieb, Carola-Bibiane. (2017). Faster PET reconstruction with a stochastic primal-dual hybrid gradient method. SPIE Proc (2017).