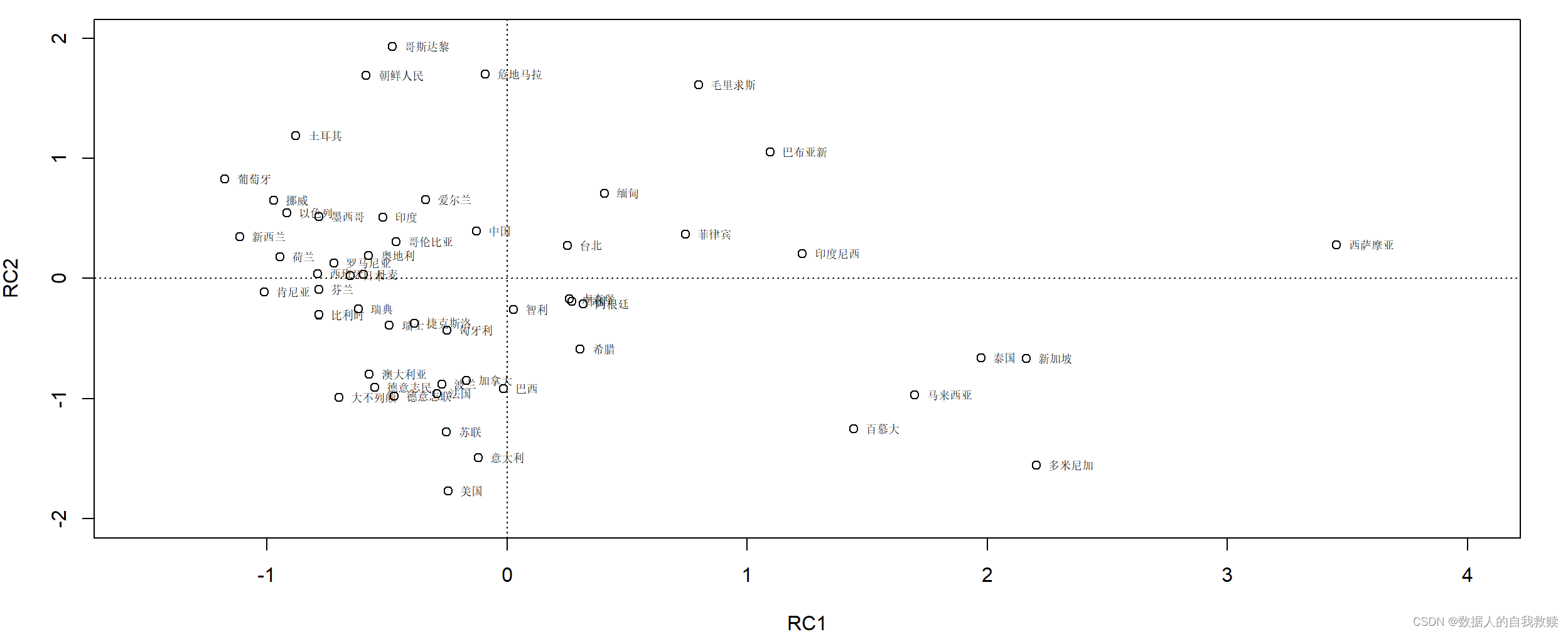
二分搜索
- Arrays.binarySearch(int[] a,int key)源码分析
- 【LeetCode】209. 长度最小的子数组
- 解法1:前缀和 + 暴力解法
- 解法2:前缀和 + 二分搜索
序:使用
Arrays工具类中的binarySearch方法进行二分搜索时,我们知道搜索成功会返回其下标,那么搜索失败它会返回什么呢?分析分析源码。
Arrays.binarySearch(int[] a,int key)源码分析
二分搜索可以针对于任何类型,但大差不差,都是几乎一致的,这里为了方便,说的是整型数据类型的二分方法。
下面聊聊源码:

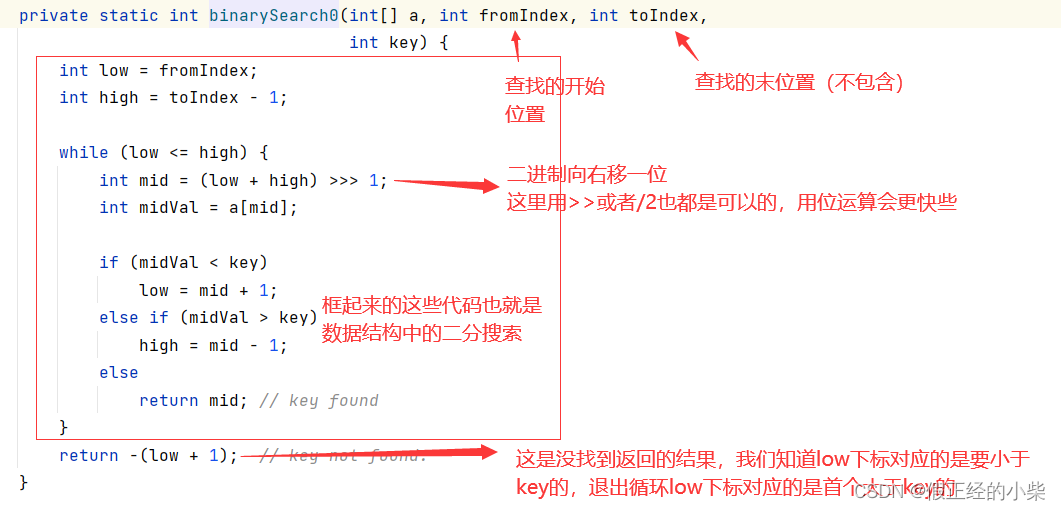
图中可以看出如果没找到返回的是-(low+1)
这里我们还可以看到low出循环是指向首个大于key的下标的,那么low+1就是大于key的第二个了(假设在数组范围内),不是我们一般想要的。
那么没找到如何通过该返回获得
low呢?
- 知道是返回
-(low+1)了,通过数学运算把结果取反-1;- 直接用位运算中的
~取反,我们知道没返回的是个负数,负数补码取反是先-1再取反,也就是-(low+1-1),一样的效果。
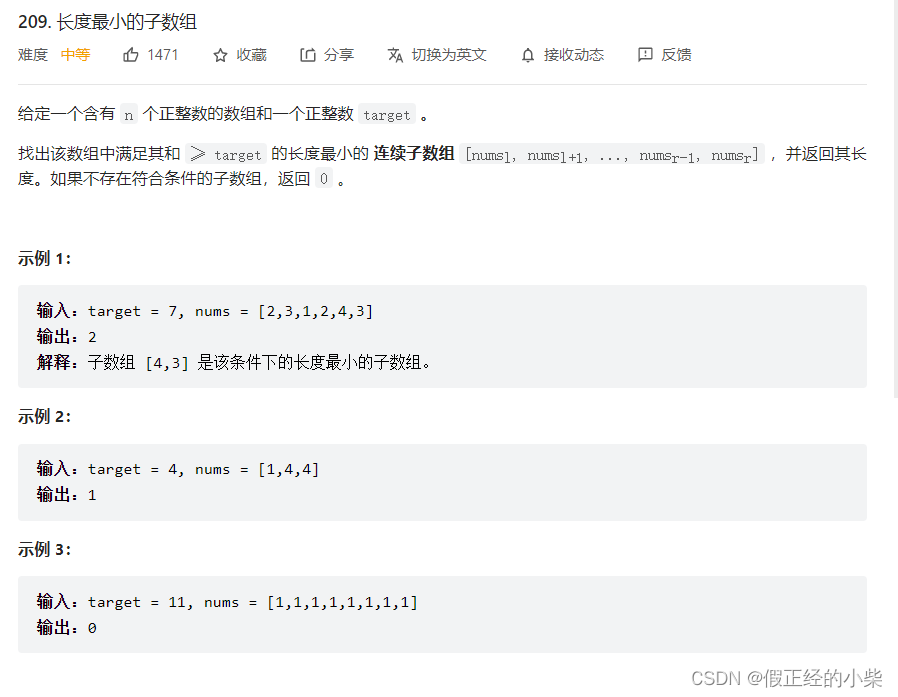
【LeetCode】209. 长度最小的子数组
题目:
解法1:前缀和 + 暴力解法
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int cnt = 0;
int[] pre = new int[nums.length+1];//前缀和
Arrays.fill(pre,0);
for(int i=0;i<nums.length;++i){
pre[i+1] = pre[i] + nums[i];
}
int minLen = 0;
for(int i=1;i<=nums.length;++i){
int sum = minLen==0?pre[i]:pre[i] - pre[i-minLen+1];//看看是否有更小的且符合条件的minLen
int left = 1;
while(sum>=target){
minLen = minLen==0?i-left+1:Math.min(minLen,i-left+1);//更新长度
sum = pre[i] - pre[left];
left++;
}
}
return minLen;
}
}
解法2:前缀和 + 二分搜索
- 求出的前缀和是升序的,满足二分有序搜索条件;
- 所求的是大于target的最小长度==》
pre[i] - pre[left]>=target==>pre[i]>=target + pre[left],也就是求满足该条件下的,i - left + 1的最小值。
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int cnt = 0;
int[] pre = new int[nums.length+1];//前缀和
Arrays.fill(pre,0);
for(int i=0;i<nums.length;++i){
pre[i+1] = pre[i] + nums[i];
}
int minLen = Integer.MAX_VALUE;
for(int i=0;i<=nums.length;++i){
int endTarget = target + pre[i];
int index = Arrays.binarySearch(pre,endTarget);
// 如果index小于零,转换一下,找到首个大于目标的第一个下标
if(index<0){
index = ~index;
}
// 判断下标是否过界,如果超过了数组范围,表示数组内全部小于endTarget
if(index<=nums.length){
minLen = Math.min(minLen,index-i);
}
}
return minLen==Integer.MAX_VALUE?0:minLen;
}
}
解法1代码进行了我进行了优化,所以运行时间未必比下面的慢,看情况各有各好处。







![[oeasy]python0022_ python虚拟机_反编译_cpu架构_二进制字节码_汇编语言](https://img-blog.csdnimg.cn/img_convert/ed53e6b51005e95514adaf4525ce37d3.png)