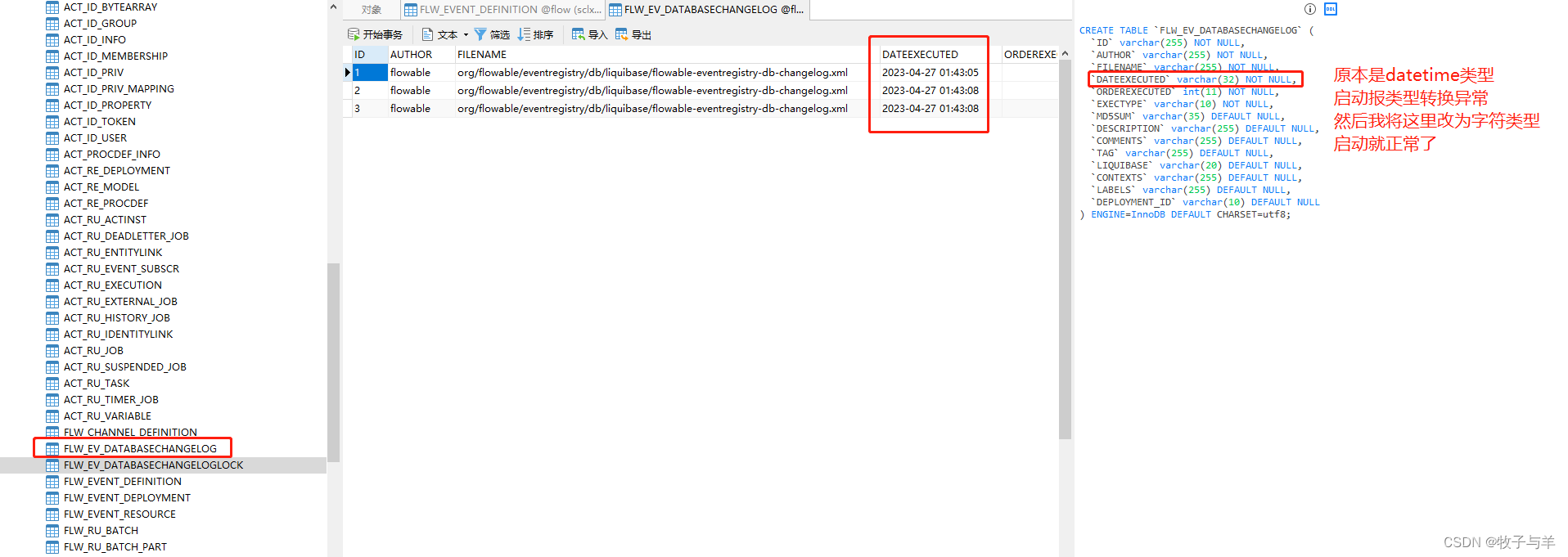
C++算法初级11——01背包问题(动态规划2)
文章目录
- C++算法初级11——01背包问题(动态规划2)
- 问题引入
- 0-1背包问题分析
- 0-1背包问题的形式化分析
- 优化
问题引入
辰辰采药
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
辰辰采药在算法中属于一种很经典的0-1背包问题。更一般的,这种问题可以转化为:
给定n个物品,每个物体有个体积v i和一个价值p i
现有一个容量为V的背包,请问如何选择物品装入背包,使得获得的总价值最大?
0-1背包问题分析
0-1背包问题描述:给定n个物品,每个物体有个体积v i和一个价值p i
现有一个容量为V的背包,请问如何选择物品装入背包,使得获得的总价值最大?
基本思路
考虑到现在我们能做的决策,只有对于每个物品的“选”与“不选”。所以,这个问题就是
- 以“将每一个物品依次放入背包”划分不同阶段
- 而对于每个物品的“选与不选”就是不同决策
考虑到所有的放置前i个物品的方案数可以分为两类:
- 一个是放第i个物品,
- 一个是不放第i个物品
所以下面我们分这两种情况来讨论。因为在决策的过程中,变化的是当前所在的阶段,以及容量的剩余大小。
所以,我们维护一个二维状态f[i,j], 来表示前i个物品,放到体积为j的背包里,可以得到的最大价值。
首先,考虑容量为任意值j时,将前i个物品放入背包的情况。

所以,状态转移方程为
f
[
i
]
[
j
]
=
m
a
x
{
f
[
i
−
1
,
j
]
,
p
[
i
]
+
f
[
i
−
1
]
[
j
−
v
[
i
]
}
f[i][j]=max\{f[i-1,j],p[i]+f[i-1][j-v[i]\}
f[i][j]=max{f[i−1,j],p[i]+f[i−1][j−v[i]}
0-1背包问题的形式化分析
使用动态规划解决问题,需要明确状态设计、转移方程、初始状态和转移方向四个方面。
那现在,让我们来明确一下该0-1背包问题中的动态规划四要素:
- 状态:
用f[i][j]表示前i个物品,放在空间为j的背包里,能获得的最大收益。 - 转移方程:
因为每一个阶段有至多两种选择,所以需要分别计算两种选择的收益后取较大值。
f[i][j] = f[i - 1][j] // j < v[i],表示装不下第i个物品
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + p[i]); // otherwise
- 初始状态:
在一个物品都没放的时候,无论背包大小多少,总价值都是0,即
f[0][j] = 0 // 0 <= j <= V
- 转移方向:
观察转移方程,发现要想保证等式右边的状态一定比左边的状态先算出来,只需要保证i从小到大计算即可。
最终该问题的答案就是f[n,V]。这样,0-1背包问题就可以使用动态规划来解决~
代码
# include <bits/stdc++.h>
using namespace std;
# define N 1002
int n=3;
int V = 70;
vector<int> v = {0,71,69,1};//体积
vector<int> p ={0,100,1,2};//价值
// 第0位,置为0,不参与计算,便于与后面的下标进行统一
int f[N][N];
int main()
{
for(int j=0;j<=V;j++)
f[0][j]=0;
for(int i=1;i<=n;i++)
{
if(v[i]>V)
continue;
for(int j=0;j<=V;j++)
{
if(j<v[i])
f[i][j]=f[i-1][j];
else
f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+p[i]);
}
}
cout<<f[n][V]<<endl;
}
动态规划的主要工作:就是算出不同状态下的结果,然后用相应维数的数组保存。
所以,整个动态规划的过程就是一个”填表“的过程。

优化

滚动数组优化
因为整个动态规划的过程就是一个填表的过程,如下图:
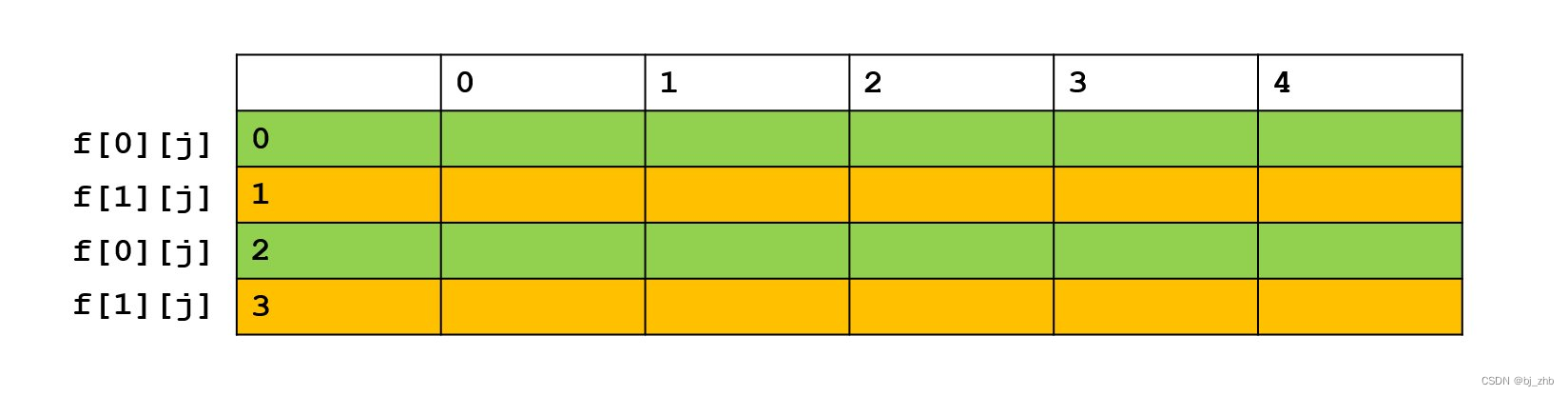
而在本题中,填表的顺序就是:填完上一行,然后填下一行。而且我们发现,下一行的状态,只会用到上一行的状态来转移。所以,当我们在计算第i行时,其实前i−2行的状态就都没必要保留了。所以,我们可以用一种类似于”踩石头过河“的思想。
试想如果我们有一些石头,想利用这些石头过河。
如果石头的数量很多,那么最方便的方法就是用这些石头铺一道石头路,这样我们就可以顺利过河。这就相当于我们可以开很充足的数组,然后把计算的每个阶段都存在数组里。
但如果我们只有两块石头,就过不了河了吗?不是的。我们可以用下图的方法一边走一边挪动石头,这样也可以顺利过河。
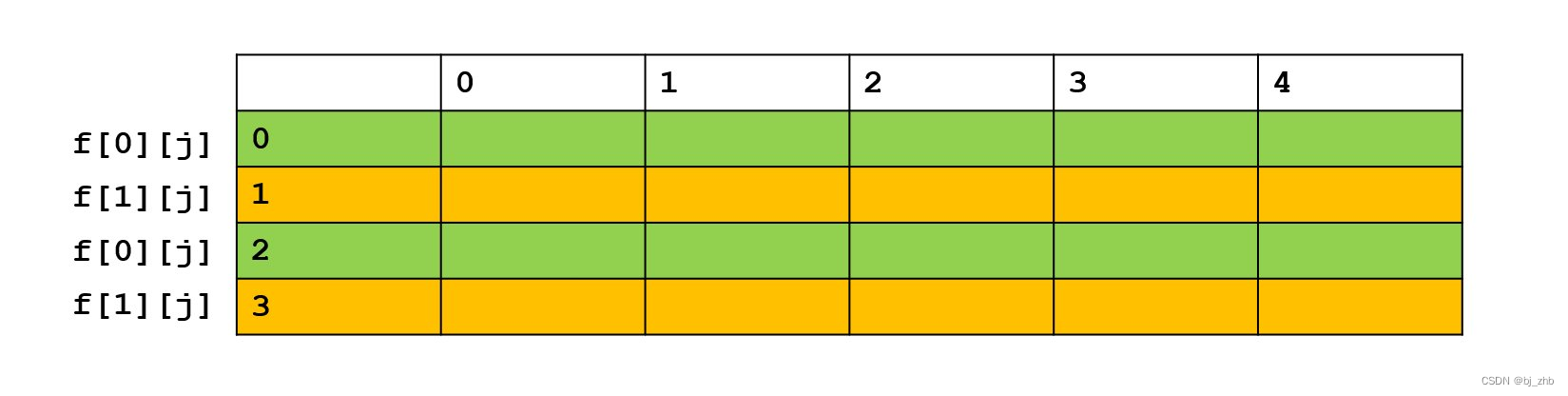
在空间优化的方法中,有一种很常见就是利用过河的思想。这种方法叫做滚动数组。在整个算法过程中,我们只用2×V的数组f[2][V]来记录状态。其中,所有奇数行的状态填入f[1][j]中,所有偶数行的状态填入f[0][j]中,如下图
# include <bits/stdc++.h>
using namespace std;
# define N 1002
int n=3;
int V = 70;
vector<int> v = {0,71,69,1};//体积
vector<int> p ={0,100,1,2};//价值
// 第0位,置为0,不参与计算,便于与后面的下标进行统一
int f[2][N];//f[i][j]表示前i个物品,体积为j的最大价值
int main()
{
for(int i=1;i<=n;i++)
{
for(int j=0;j<=V;j++)
{
if(j<v[i])
f[i&1][j] = f[(i-1)&1][j];
else
f[i&1][j] = max(f[(i-1)&1][j],f[(i-1)&1][j-v[i]]+p[i]);
}
}
cout<<f[n&1][V]<<endl;
return 0;
}
算法优化2 —— 优化到一维数组
那么我们可不可以再进一步优化空间,使得只用一个一维数组就能解决整个问题了呢?
想到之前“踩石头过河”的类比,我们可能会觉得不太可能。但是如果我们进一步分析整个表的填写,如下图:
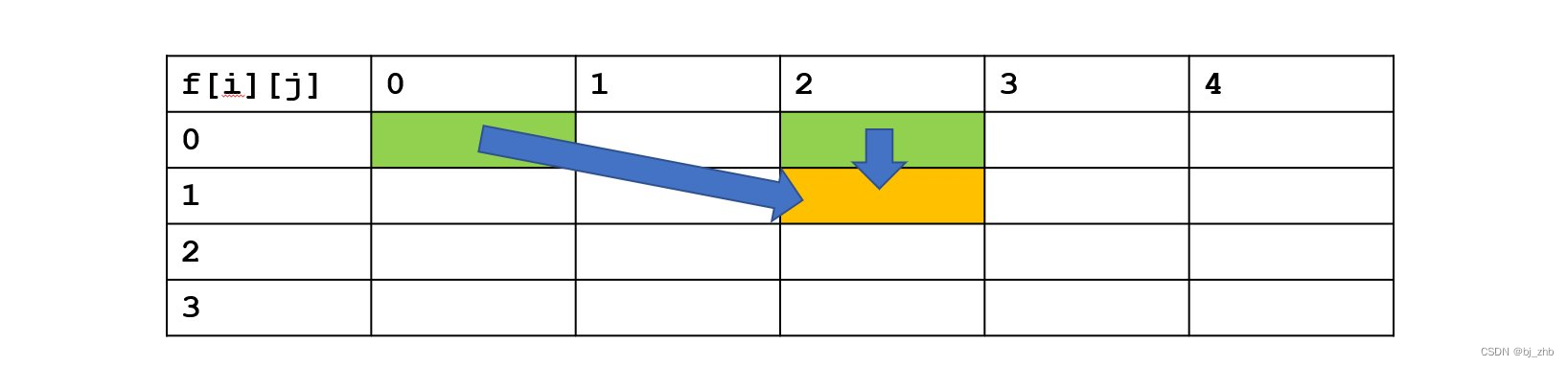
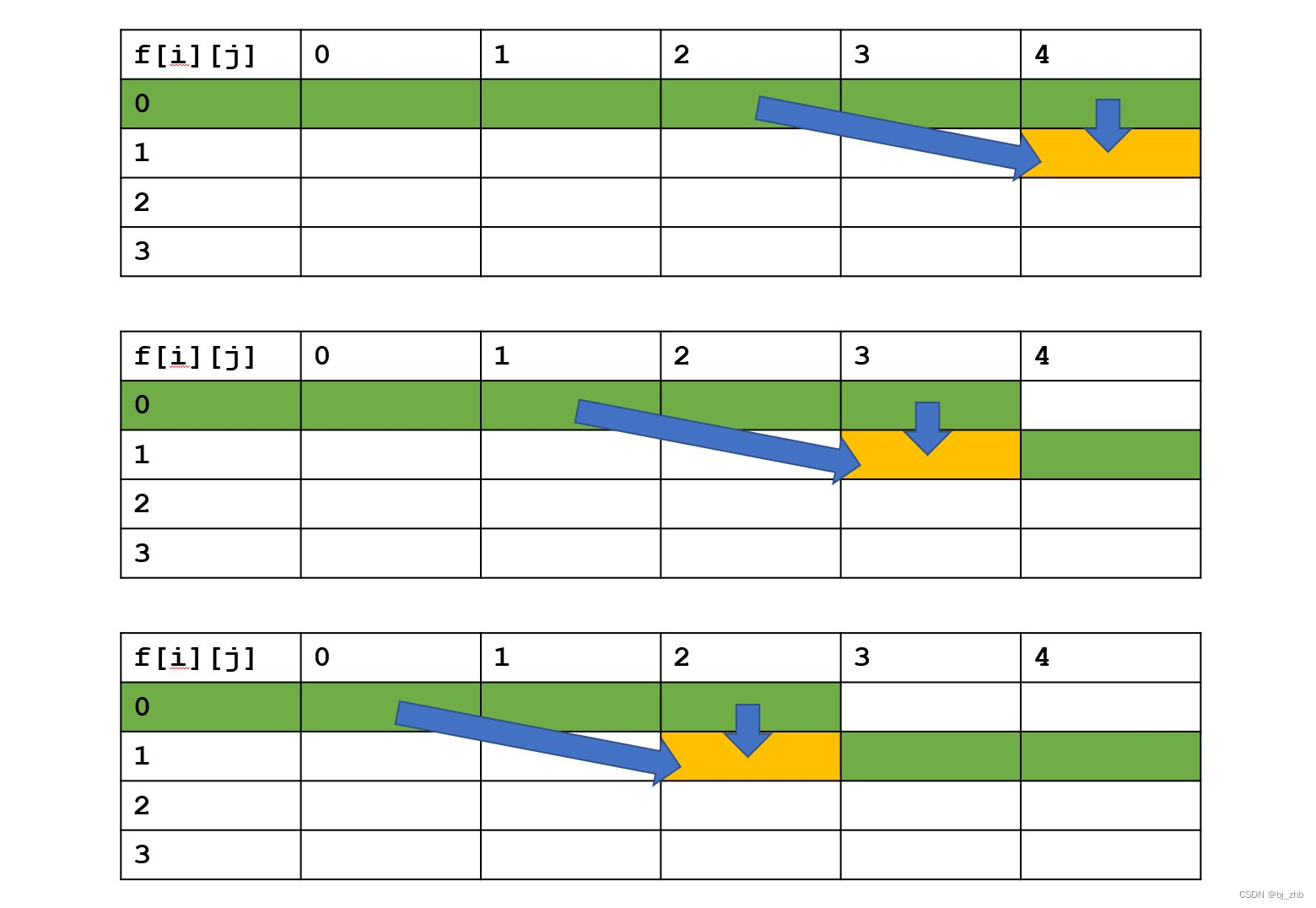
会发现下一行的某个状态,正好是由它上面的元素,以及左上方的某个元素转移而来。所以我们需要保证当计算黄色状态时上面两个绿色状态没有被覆盖掉。所以,当我们计算第i行时,完全可以将j从大到小枚举,这样在计算状态f(i,j)之前,数组f[j]中存储的是状态f[i−1,j],更新完以后,
f[j]中存的状态就是f[i,j]了。如下图:
# include <bits/stdc++.h>
using namespace std;
# define N 1002
int n=3;
int V = 70;
vector<int> v = {0,71,69,1};//体积
vector<int> p ={0,100,1,2};//价值
// 第0位,置为0,不参与计算,便于与后面的下标进行统一
int f[N];
int main()
{
for(int i=1;i<=n;i++)
{
for(int j=V;j>=v[i];j--)
{
f[j] = max(f[j],f[j-v[i]]+p[i]);
}
}
cout<<f[V]<<endl;
return 0;
}

![C嘎嘎~~[类 中篇]](https://img-blog.csdnimg.cn/4820ec7769e145649ebe3453a22b14d8.png)