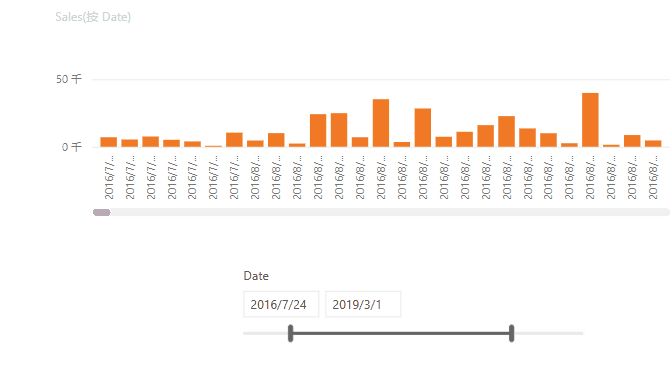
题目描述

给定两个整数数组a和b，计算具有最小差绝对值的一对数值（每个数组中取一个值），并返回该对数值的差

示例：

输入：{1, 3, 15, 11, 2}, {23, 127, 235, 19, 8}
输出：3，即数值对(11, 8)

提示：

1 <= a.length, b.length <= 100000
-2147483648 <= a[i], b[i] <= 2147483647
正确结果在区间 [0, 2147483647] 内

解题思路与代码

这道题呢，首先从正常的思路想嘛，看看能不能暴力破解。也就是两层for循环解决问题。我试了，发现不行。好的那我们就另找方法。

根据这道题的题意。我总结出来两种做题的方法，一种是合并两个数组，然后统一排序，之后遍历整个数组就好了。另一种是给两个数组分别排序，用双指针去遍历数组解决这道问题。

方法一：合并 + 排序

我们这里用到了vector<pair<int,char>>这样的数据结构来解决这个问题。如果说，小伙伴们对pair这种数据结构了解了话，一看到这个，可能就脑子里直接就有答案了。
我们分别把a，b两个数组遍历进合并数组vec中，用sort给它进行排个序。之后挨个元素进行比较就行了。

具体实现请看代码：

class Solution {
public:
    int smallestDifference(vector<int>& a, vector<int>& b) {
        vector<pair<int,char>> vec;
        for(int i = 0; i < a.size(); ++i)
            vec.push_back({a[i],'a'});
        for(int i = 0; i < b.size(); ++i)
            vec.push_back({b[i],'b'});

        sort(vec.begin(),vec.end(),[](const pair<int,char>& l, const pair<int,char>& r) -> bool{ return l.first < r.first;});
        
        int minAbs = INT_MAX;
        for(int i = 1; i < vec.size(); ++i){
            long long vec1 = vec[i-1].first;
            long long vec2 = vec[i].first;
            if(vec[i-1].second != vec[i].second){
                if( vec2 - vec1 > 2147483648) continue;
                else if(vec2 - vec1 < minAbs) minAbs = vec2 - vec1;
            }
        }
        return minAbs;
    }
};

在这里插入图片描述

复杂度分析

时间复杂度：

我们将数组a的元素个数记作n，数组b的元素记作m
第一个for循环，将数组a中的元素放入vec中，需要O(n)的时间。
第二个for循环，将数组b中的元素放入vec中，需要O(m)的时间。
对vec进行排序，时间复杂度为O((n + m) * log(n + m))。
最后一个for循环，遍历整个vec，时间复杂度为O(n + m)。

总的时间复杂度为O((n + m) * log(n + m))。

空间复杂度：

vec数组的长度为n + m，空间复杂度为O(n + m)。除了vec数组，其他变量所占用的空间可以忽略不计。所以总的空间复杂度为O(n + m)。

方法二：排序 + 双指针

在这种方法里，我们先分别将数组a，b中的元素进行排序，之后设置两个指针，分别指向两个数组的首元素。
我们使用一个while循环去遍历两个指针，当两个指针中的任意一个走到头时，就结束此次遍历。
我们每次遍历，都拿a中的元素去减b中的元素，如果是负数，a向前走一步，反之，b向前走一步。每走一步，都计算一次差值，并每次都去与之前的差值进行比较，找出最小的那一个。
遍历完成后返回

具体的代码如下：

class Solution {
public:
    int smallestDifference(vector<int>& a, vector<int>& b) {
        sort(a.begin(),a.end());
        sort(b.begin(),b.end());
        long long minSub = INT_MAX;
        int p1 = 0;
        int p2 = 0;
        while(p1 < a.size() && p2 < b.size()){
            long long sub = a[p1] - b[p2];
            if(sub < 0) ++p1;
            else if(sub > 0) ++p2;
            else return 0;
            minSub = min(minSub,abs(sub));
        }
        return minSub;
    }
};

在这里插入图片描述

复杂度分析

这段代码实现了一个名为smallestDifference的函数，用于求两个整数数组a和b中分别取一个数，使得它们之间的差的绝对值最小。我们将使用n和m分别代表数组a和数组b的元素个数，分析这段代码的最简时间复杂度和空间复杂度。

时间复杂度：

对数组a进行排序，时间复杂度为O(n * log(n))。
对数组b进行排序，时间复杂度为O(m * log(m))。
while循环，在最坏情况下（即数组a和数组b中的元素没有相等的数），需要遍历整个数组a和数组b，时间复杂度为O(n + m)。
合并后的总时间复杂度为：O(n * log(n) + m * log(m) + n + m)。在表示最简时间复杂度时，我们可以忽略线性项n和m，因为它们相对于n * log(n)和m * log(m)的影响较小。因此，最简时间复杂度为O(n * log(n) + m * log(m))。

空间复杂度：