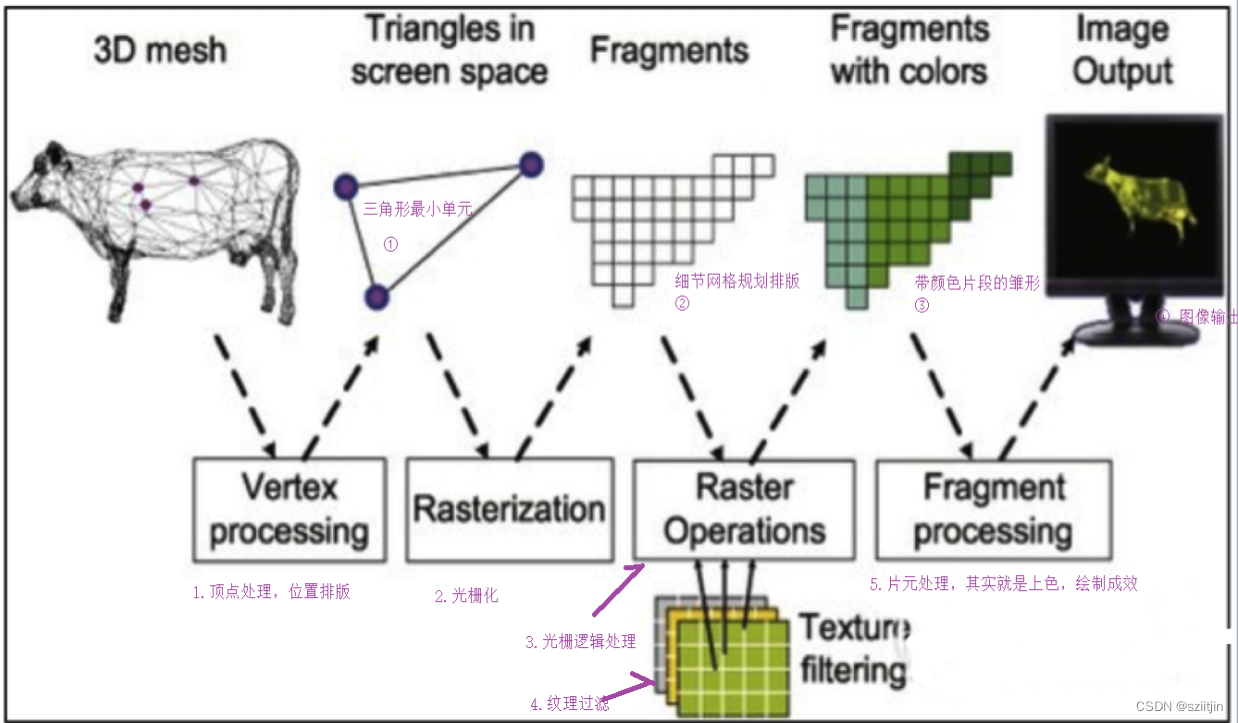
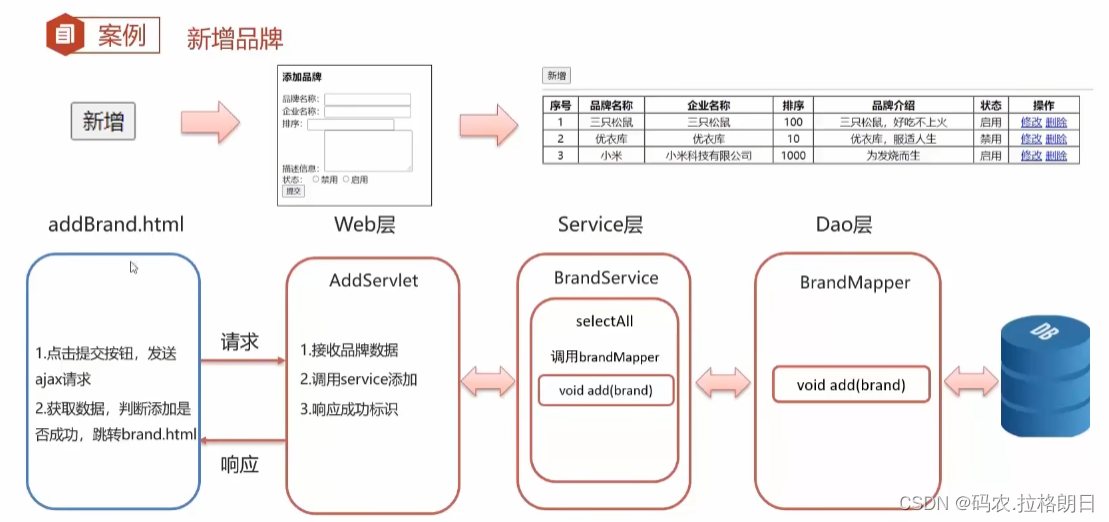
0 概述

随机算法涉及大量概率论知识，有时候难得去仔细看推导过程，当然能够完全了解推导的过程自然是有好处的，如果不了解推导过程，至少记住结论也是必要的。本文总结最常见的一些随机算法的题目，是几年前找工作的时候写的。需要说明的是，这里用到的随机函数 randInt(a, b) 假定它能随机的产生范围 [a,b] 内的整数，即产生每个整数的概率相等（虽然在实际中并不一定能实现，不过不要太在意，这个世界很多事情都很随机）。

1 随机排列数组

假设给定一个数组 A，它包含元素 1 到 N，我们的目标是构造这个数组的一个均匀随机排列。

一个常用的方法是为数组每个元素 A[i] 赋一个随机的优先级 P[i]，然后依据优先级对数组进行排序。比如我们的数组为 A = {1， 2， 3， 4}，如果选择的优先级数组为 P = {36， 3， 97， 19}，那么就可以得到数列 B={2, 4, 1, 3}，因为 3 的优先级最高（为97），而 2 的优先级最低（为3）。这个算法需要产生优先级数组，还需使用优先级数组对原数组排序，这里就不详细描述了，还有一种更好的方法可以得到随机排列数组。

产生随机排列数组的一个更好的方法是原地排列（in-place）给定数组，可以在 O(N) 的时间内完成。伪代码如下：

RANDOMIZE-IN-PLACE ( A , n ) 
	for i ←1 to n do 
		swap A[i] ↔ A[RANDOM(i , n )]

如代码中所示，第 i 次迭代时，元素 A[i] 是从元素 A[i...n]中随机选取的，在第 i 次迭代后，我们就再也不会改变 A[i]。

A[i] 位于任意位置j的概率为 1/n。这个是很容易推导的，比如 A[1] 位于位置 1 的概率为 1/n，这个显然，因为 A[1] 不被1到n的元素替换的概率为 1/n，而后就不会再改变 A[1] 了。而A[1] 位于位置 2 的概率也是 1/n，因为 A[1] 要想位于位置2，则必须在第一次与 A[k] (k=2…n) 交换，同时第二次 A[2] 与 A[k]替换，第一次与 A[k] 交换的概率为(n-1)/n，而第二次替换概率为 1/(n-1)，所以总的概率是 (n-1)/n * 1/(n-1) = 1/n。同理可以推导其他情况。

当然这个条件只能是随机排列数组的一个必要条件，也就是说，满足元素 A[i] 位于位置 j 的概率为1/n 不一定就能说明这可以产生随机排列数组。因为它可能产生的排列数目少于 n!，尽管概率相等，但是排列数目没有达到要求，算法导论上面有一个这样的反例。

算法 RANDOMIZE-IN-PLACE可以产生均匀随机排列，它的证明过程如下：

首先给出k排列的概念，所谓 k 排列就是从n个元素中选取k个元素的排列，那么它一共有 n!/(n-k)! 个 k 排列。

循环不变式：for循环第i次迭代前，对于每个可能的i-1排列，子数组A[1…i-1]包含该i-1排列的概率为 (n-i+1)! / n!。

初始化：在第一次迭代前，i=1，则循环不变式指的是对于每个0排列，子数组A[1…i-1]包含该0排列的概率为 (n-1+1)! / n! = 1。A[1…0]为空的数组，0排列则没有任何元素，因此A包含所有可能的0排列的概率为1。不变式成立。
维持：假设在第i次迭代前，数组的i-1排列出现在 A[1...i-1] 的概率为 (n-i+1) !/ n!，那么在第i次迭代后，数组的所有i排列出现在 A[1...i] 的概率为 (n-i)! / n!。下面来推导这个结论：
- 考虑一个特殊的 i 排列 p = {x₁, x₂, … x_i}，它由一个 i-1 排列 p’ ={x1, x2,…, x_i−1} 后面跟一个 x_i 构成。设定两个事件变量E1和E2：
E1为该算法将排列 p' 放置到 A[1...i-1]的事件，概率由归纳假设得知为 Pr(E1) = (n-i+1)! / n!。
E2为在第 i 次迭代时将 x_i 放入到 A[i] 的事件。
因此我们得到 i 排列出现在 A[1...i] 的概率为 Pr {E2 ∩ E1} = Pr {E2 | E1} Pr {E1}。而Pr {E2 | E1} = 1/(n − i + 1)，所以
Pr {E2 ∩ E1} = Pr {E2 | E1} Pr {E1}= 1 /(n − i + 1) * (n − i + 1)! / n! = (n − i )! / n!。
结束：结束的时候 i=n+1，因此可以得到 A[1...n] 是一个给定 n 排列的概率为 1/n！。

C实现代码如下：

void randomInPlace(int a[], int n)
{
    int i;
    for (i = 0; i < n; i++) {
        int rand = randInt(i, n-1);
        swapInt(a, i, rand);
    }
}

扩展

如果上面的随机排列算法写成下面这样，是否也能产生均匀随机排列？

PERMUTE-WITH-ALL( A , n ) 
	for i ←1 to n do 
		swap A[i] ↔A[RANDOM(1 , n )]

注意，该算法不能产生均匀随机排列。假定 n=3，则该算法可以产生3*3*3=27个输出，而3个元素只有3!=6个不同的排列，要使得这些排列出现概率等于 1/6，则必须使得每个排列出现次数 m 满足m/27=1/6，显然，没有这样的整数符合条件。而实际上各个排列出现的概率如下，如 {1,2,3} 出现的概率为4/27，不等于 1/6。

排列	概率
<1, 2, 3>	4/27
<1, 3, 2>	5/27
<2, 1, 3>	5/27
<2, 3, 1>	5/27
❤️, 1, 2>	4/27
❤️, 2, 1>	4/27

2 随机选取一个数字

题：给定一个未知长度的整数流，如何随机选取一个数？（所谓随机就是保证每个数被选取的概率相等）

解1： 如果数据流不是很长，可以存在数组中，然后再从数组中随机选取。当然题目说的是未知长度，所以如果长度很大不足以保存在内存中的话，这种解法有其局限性。

解2： 如果数据流很长的话，可以这样：

如果数据流在第1个数字后结束，那么必选第1个数字。
如果数据流在第2个数字后结束，那么我们选第2个数字的概率为1/2，我们以1/2的概率用第2个数字替换前面选的随机数，得到新的随机数。
…
如果数据流在第n个数字后结束，那么我们选择第n个数字的概率为1/n，即我们以1/n的概率用第n个数字替换前面选的随机数，得到新的随机数。

一个简单的方法就是使用随机函数 f(n)=bigrand()%n，其中 bigrand() 返回很大的随机整数，当数据流到第 n 个数时，如果 f(n)==0，则替换前面的已经选的随机数，这样可以保证每个数字被选中的概率都是 1/n。如当 n=1 时，则f(1)=0，则选择第 1 个数，当 n=2 时，则第 2 个数被选中的概率都为 1/2，以此类推，当数字长度为 n 时，第 n 个数字被选中的概率为 1/n。代码如下(注：在 Linux/MacOS 下，rand() 函数已经可以返回一个很大的随机数了，就当做bigrand()用了)：

void randomOne(int n)
{
    int i, select = 0;
    for (i = 1; i < n; i++) {
        int rd = rand() % n;
        if (rd == 0) {
            select = i;
        }
    }
    printf("%d\n", select);
}

3 随机选取M个数字

题：程序输入包含两个整数 m 和 n ，其中 m<n，输出是 0~n-1 范围内的 m 个随机整数的有序列表，不允许重复。从概率角度来说，我们希望得到没有重复的有序选择，其中每个选择出现的概率相等。

解1： 先考虑个简单的例子，当 m=2，n=5 时，我们需要从 0~4 这 5 个整数中等概率的选取 2 个有序的整数，且不能重复。如果采用如下条件选取：bigrand() % 5 < 2，则我们选取 0 的概率为2/5。但是我们不能采取同样的概率来选取 1，因为选取了 0 后，我们应该以 1/4 的概率来选取1，而在没有选取0的情况下，我们应该以 2/4 的概率选取1。选取的伪代码如下：

select = m
remaining = n
for i = [0, n)
    if (bigrand() % remaining < select)
         print i
         select--
    remaining--

只要满足条件 m<=n，则程序输出 m 个有序整数，不多不少。不会多选，因为每选择一个数，select--，这样当 select 减到 0 后就不会再选了。同时，也不会少选，因为每次都会remaining--，当 select/remaining=1 时，一定会选取一个数。每个子集被选择的概率是相等的，比如这里5选2则共有 C(5,2)=10 个子集，如 {0，1}，{0，2}...等，每个子集被选中的概率都是 1/10。

更一般的推导，n选m的子集数目一共有 C(n,m) 个，考虑一个特定的 m 序列，如0...m-1，则选取它的概率为m/n * (m-1)/(n-1)*....1/(n-m+1)=1/C(n,m)，可以看到概率是相等的。

Knuth 老爷爷很早就提出了这个算法，他的实现如下：

void randomMKnuth(int n, int m)
{
    int i;
    for (i = 0; i < n; i++) {
        if ((rand() % (n-i)) < m) {
            printf("%d ", i);
            m--;
        }
    }
}

解2： 还可以采用前面随机排列数组的思想，先对前 m 个数字进行随机排列，然后排序这 m 个数字并输出即可。代码如下：

void randomMArray(int n, int m)
{
    int i, j;
    int *x = (int *)malloc(sizeof(int) * n);
    
    for (i = 0; i < n; i++)
        x[i] = i;

    // 随机数组
    for (i = 0; i < m; i++) {
        j = randInt(i, n-1);
        swapInt(x, i, j);
    }

    // 对数组前 m 个元素排序
    for (i = 0; i < m; i++) {
        for (j = i+1; j>0 && x[j-1]>x[j]; j--) {
            swapInt(x, j, j-1);
        }
    }

    for (i = 0; i < m; i++) {
        printf("%d ", x[i]);
    }

    printf("\n");
}

4 rand7 生成 rand10 问题

题：已知一个函数rand7()能够生成1-7的随机数，每个数概率相等，请给出一个函数rand10()，该函数能够生成 1-10 的随机数，每个数概率相等。

解1： 要产生 1-10 的随机数，我们要么执行 rand7() 两次，要么直接乘以一个数字来得到我们想要的范围值。如下面公式(1)和（2）。

idx = 7 * (rand7()-1) + rand7() ---(1) 正确
idx = 8 * rand7() - 7           ---(2) 错误

上面公式 (1) 能够产生 1-49 的随机数，为什么呢？因为 rand7() 的可能的值为 1-7，两个 rand7() 则可能产生 49 种组合，且正好是 1-49 这 49 个数，每个数出现的概率为 1/49，于是我们可以将大于 40 的丢弃，然后取 (idx-1) % 10 + 1 即可。公式（2）是错误的，因为它生成的数的概率不均等，而且也无法生成49个数字。

   1  2  3  4  5  6  7
1  1  2  3  4  5  6  7
2  8  9 10  1  2  3  4
3  5  6  7  8  9 10  1
4  2  3  4  5  6  7  8
5  9 10  1  2  3  4  5
6  6  7  8  9 10  *  *
7  *  *  *  *  *  *  *

该解法基于一种叫做拒绝采样的方法。主要思想是只要产生一个目标范围内的随机数，则直接返回。如果产生的随机数不在目标范围内，则丢弃该值，重新取样。由于目标范围内的数字被选中的概率相等，这样一个均匀的分布生成了。代码如下：

int rand7ToRand10Sample() {
    int row, col, idx;
    do {
        row = rand7();
        col = rand7();
        idx = col + (row-1)*7;
    } while (idx > 40);

    return 1 + (idx-1) % 10;
}

由于row范围为1-7，col范围为1-7，这样idx值范围为1-49。大于40的值被丢弃，这样剩下1-40范围内的数字，通过取模返回。下面计算一下得到一个满足1-40范围的数需要进行取样的次数的期望值：

E(# calls to rand7) = 2 * (40/49) +
                      4 * (9/49) * (40/49) +
                      6 * (9/49)2 * (40/49) +
                      ...

                      ∞
                    = ∑ 2k * (9/49)k-1 * (40/49)
                      k=1

                    = (80/49) / (1 - 9/49)2
                    = 2.45

解2： 上面的方法大概需要2.45次调用 rand7 函数才能得到 1 个 1-10 范围的数，下面可以进行再度优化。对于大于40的数，我们不必马上丢弃，可以对 41-49 的数减去 40 可得到 1-9 的随机数，而rand7可生成 1-7 的随机数，这样可以生成 1-63 的随机数。对于 1-60 我们可以直接返回，而 61-63 则丢弃，这样需要丢弃的数只有3个，相比前面的9个，效率有所提高。而对于61-63的数，减去60后为 1-3，rand7 产生 1-7，这样可以再度利用产生 1-21 的数，对于 1-20 我们则直接返回，对于 21 则丢弃。这时，丢弃的数就只有1个了，优化又进一步。当然这里面对rand7的调用次数也是增加了的。代码如下，优化后的期望大概是 2.2123。

int rand7ToRand10UtilizeSample() {
    int a, b, idx;
    while (1) {
        a = randInt(1, 7);
        b = randInt(1, 7);
        idx = b + (a-1)*7;
        if (idx <= 40)
            return 1 + (idx-1)%10;

        a = idx-40;
        b = randInt(1, 7);
        // get uniform dist from 1 - 63
        idx = b + (a-1)*7;
        if (idx <= 60)
            return 1 + (idx-1)%10;

        a = idx-60;
        b = randInt(1, 7);
        // get uniform dist from 1-21
        idx = b + (a-1)*7;
        if (idx <= 20)
            return 1 + (idx-1)%10;
    }
}

5 趣味概率题

1）称球问题

题：有12个小球，其中一个是坏球。给你一架天平，需要你用最少的称次数来确定哪个小球是坏的，并且它到底是轻了还是重了。

解：之前有总结过二分查找算法，我们知道二分法可以加快有序数组的查找。相似的，比如在数字游戏中，如果要你猜一个介于 1-64 之间的数字，用二分法在6次内肯定能猜出来。但是称球问题却不同。称球问题这里 12 个小球，坏球可能是其中任意一个，这就有 12 种可能性。而坏球可能是重了或者轻了这2种情况，于是这个问题一共有 12*2 = 24 种可能性。每次用天平称，天平可以输出的是 平衡、左重、右重 3 种可能性，即称一次可以将问题可能性缩小到原来的 1/3，则一共 24 种可能性可以在 3 次内称出来(3^3 = 27)。

为什么最直观的称法 6-6 不是最优的？在 6-6 称的时候，天平平衡的可能性是0，而最优策略应该是让天平每次称量时的概率均等，这样才能三等分答案的所有可能性。

具体怎么实施呢？将球编号为1-12，采用 4, 4 称的方法。

我们先将 1 2 3 4 和 5 6 7 8 进行第1次称重。
如果第1次平衡，则坏球肯定在 9-12 号中。则此时只剩下 9-12 4个球，可能性为 9- 10- 11- 12- 9+ 10+ 11+ 12+ 这8种可能。接下来将 9 10 11 和 1 2 3称第2次：如果平衡，则 12 号小球为坏球，将12号小球与1号小球称第3次即可确认轻还是重。如果不平衡，则如果重了说明坏球重了，继续将9和10号球称量，重的为坏球，平衡的话则11为坏球。
如果第1次不平衡，则坏球肯定在 1-8号中。则还剩下的可能性是 1+ 2+ 3+ 4+ 5- 6- 7- 8- 或者 1- 2- 3- 4- 5+ 6+ 7+ 8+，如果是1 2 3 4 这边重，则可以将 1 2 6 和 3 4 5 称，如果平衡，则必然是 7 8 轻了，再称一次7和1，便可以判断7和8哪个是坏球了。如果不平衡，假定是 1 2 6 这边重，则可以判断出 1 2 重了或者 5 轻了，为什么呢？因为如果是3+ 4+ 6-，则 1 2 3 4 比 5 6 7 8 重，但是 1 2 6 应该比 3 4 5 轻。其他情况同理，最多3次即可找出坏球。

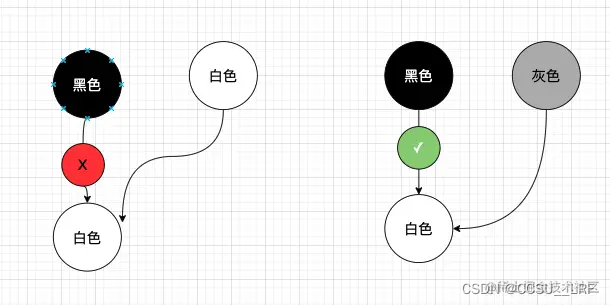
下面这个图更加清晰说明了这个原理。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NecW12n8-1682522423467)(null)]

2）生男生女问题

题：在重男轻女的国家里，男女的比例是多少？在一个重男轻女的国家里，每个家庭都想生男孩，如果他们生的孩子是女孩，就再生一个，直到生下的是男孩为止。这样的国家，男女比例会是多少？

解：还是1：1。在所有出生的第一个小孩中，男女比例是1：1；在所有出生的第二个小孩中，男女比例是1：1；… 在所有出生的第n个小孩中，男女比例还是1：1。所以总的男女比例是1：1。

3）约会问题

题：两人相约5点到6点在某地会面，先到者等20分钟后离去，求这两人能够会面的概率。

解：设两人分别在5点X分和5点Y分到达目的地，则他们能够会面的条件是 |X-Y| <= 20，而整个范围为 S={(x, y): 0 =< x <= 60, 0=< y <= 60}，如果画出坐标轴的话，会面的情况为坐标轴中表示的面积，概率为 (60^2 - 40^2) / 60^2 = 5/9。

4）帽子问题

题：有n位顾客，他们每个人给餐厅的服务生一顶帽子，服务生以随机的顺序归还给顾客，请问拿到自己帽子的顾客的期望数是多少？

解：使用指示随机变量来求解这个问题会简单些。定义一个随机变量X等于能够拿到自己帽子的顾客数目，我们要计算的是 E[X]。对于 i=1, 2 ... n，定义 X_i =I {顾客i拿到自己的帽子}，则 X=X₁+X₂+…X_n。由于归还帽子的顺序是随机的，所以每个顾客拿到自己帽子的概率为1/n，即 P_r(X_i=1)=1/n，从而 E(X_i)=1/n，所以E(X)=E(X₁ + X₂ + …X_n)= E(X₁)+E(X₂)+…E(X_n)=n*1/n = 1，即大约有1个顾客可以拿到自己的帽子。

5）生日悖论

题：一个房间至少要有多少人，才能使得有两个人的生日在同一天？

解：对房间k个人中的每一对(i, j)定义指示器变量 X_ij = {i与j生日在同一天} ，则i与j生日相同时，X_ij=1，否则 X_ij=0。两个人在同一天生日的概率 Pr(X_ij=1)=1/n 。则用X表示同一天生日的两人对的数目，则 E(X)=E(∑k_i=1∑k_j=i+1X_ij) = C(k,2)*1/n = k(k-1)/2n，令 k(k-1)/2n >=1，可得到 k>=28，即至少要有 28 个人，才能期望两个人的生日在同一天。