目录
- 一、问题描述
- 二、Elman网络预测上证股市开盘价原理
- 三、算法步骤
- 3.1 加载数据
- 3.2 构造样本集
- 3.3 划分训练集和测试集
- 3.4 创建Elman神经网络
- 3.5 网络训练
- 3.6 测试
- 四、结果展示
一、问题描述
选择2005年6月30日至2006年12月1日的上证开盘价进行预测分析。数据保存在elm_stock.mat文件中,共计337条开盘价格,保存为double类型的向量中,开盘价的走势如下图所示。


二、Elman网络预测上证股市开盘价原理
采用过去的股价预测下一期股价,因此相当于一个时间序列问题,可以用Elman神经网络求解。
x
n
=
f
(
x
n
−
1
,
x
n
−
2
,
x
n
−
N
)
{x_n} = f\left( {{x_{n - 1}},{x_{n - 2}},{x_{n - N}}} \right)
xn=f(xn−1,xn−2,xn−N)
对于给定的337条开盘价数据,首先将其划分为训练样本和测试样本。以训练样本为例,抽取
x
1
∼
x
N
{x_1} \sim{x_N}
x1∼xN组成第一个样本,其中
(
x
1
,
x
2
,
⋯
,
x
N
−
1
)
\left( {{x_1},{x_2}, \cdots ,{x_{N - 1}}} \right)
(x1,x2,⋯,xN−1)为自变量,
x
N
{x_N}
xN为目标函数值;抽取
x
2
∼
x
N
+
1
{x_2} \sim{x_{N+1}}
x2∼xN+1组成第二个样本,其中
(
x
2
,
x
3
,
⋯
,
x
N
)
\left( {{x_2},{x_3}, \cdots ,{x_{N}}} \right)
(x2,x3,⋯,xN)为自变量,
x
N
+
1
{x_{N+1}}
xN+1为函数值,以此类推,最终形成以下训练矩阵:
[
x
1
x
2
x
i
x
2
x
3
x
i
+
1
⋯
⋯
⋯
x
N
−
1
x
N
x
N
x
N
+
1
]
\left[ \begin{array}{l} {x_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_i}\\ {x_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_3}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_{i + 1}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots \\ {x_{N - 1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_N}\\ {x_N}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_{N + 1}} \end{array} \right]
x1x2xix2x3xi+1⋯⋯⋯xN−1xNxNxN+1
主要流程图如下:
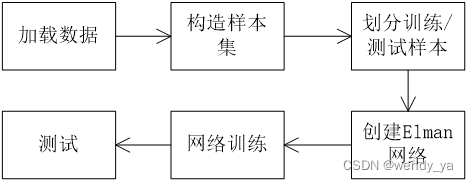
三、算法步骤
主要步骤如下:
3.1 加载数据
代码如下:
%% 清除工作空间中的变量和图形
clear,clc
close all
% 加载337个上证指数开盘价格
load elm_stock
whos
列出当前工作空间中的变量:
Name Size Bytes Class Attributes
price 337x1 2696 double
3.2 构造样本集
抽取 x 1 ∼ x N {x_1} \sim{x_N} x1∼xN组成第一个样本,其中 ( x 1 , x 2 , ⋯ , x N − 1 ) \left( {{x_1},{x_2}, \cdots ,{x_{N - 1}}} \right) (x1,x2,⋯,xN−1)为自变量, x N {x_N} xN为目标函数值,以此类推,代码如下:
% 数据个数
n=length(price);
% 确保price为列向量
price=price(:);
% x(n) 由x(n-1),x(n-2),...,x(n-L)共L个数预测得到.
L = 6;
% price_n:每列为一个构造完毕的样本,共n-L个样本
price_n = zeros(L+1, n-L);
for i=1:n-L
price_n(:,i) = price(i:i+L);
end
这里取N=6,即当期的开盘价,应由当期之前6期的开盘价计算得到。这一步将最初长度为337向量转化为7x331矩阵。
3.3 划分训练集和测试集
将前380份样本作为训练样本,最后51分样本作为测试样本 :
trainx = price_n(1:6, 1:280);
trainy = price_n(7, 1:280);
testx = price_n(1:6, 290:end);
testy = price_n(7, 290:end);
3.4 创建Elman神经网络
MATLAB神经网络工具箱提供了newelm与elmannet函数,都可以建立Elman反馈网络。这里采用elmannet函数,它只需要三个参数,分别指定延迟、隐含层神经元个数和训练函数。
% 包含15个神经元,训练函数为traingdx
net=elmannet(1:2,15,'traingdx');
% 设置显示级别
net.trainParam.show=1;
% 最大迭代次数为2000次
net.trainParam.epochs=2000;
% 误差容限,达到此误差就可以停止训练
net.trainParam.goal=0.00001;
% 最多验证失败次数
net.trainParam.max_fail=5;
% 对网络进行初始化
net=init(net);
3.5 网络训练
先归一化再训练。
%训练数据归一化
[trainx1, st1] = mapminmax(trainx);
[trainy1, st2] = mapminmax(trainy);
% 测试数据做与训练数据相同的归一化操作
testx1 = mapminmax('apply',testx,st1);
testy1 = mapminmax('apply',testy,st2);
% 输入训练样本进行训练
[net,per] = train(net,trainx1,trainy1);
训练过程如下:

3.6 测试
进行测试时应使用归一化后的数据,得出实际输出后再将输出结果反归一化为正常的数据。
% 将训练数据输入网络进行测试
train_ty1 = sim(net, trainx1);
train_ty = mapminmax('reverse', train_ty1, st2);
% 将测试数据输入网络进行测试
test_ty1 = sim(net, testx1);
test_ty = mapminmax('reverse', test_ty1, st2);
四、结果展示
预测值与真实值比较如下:
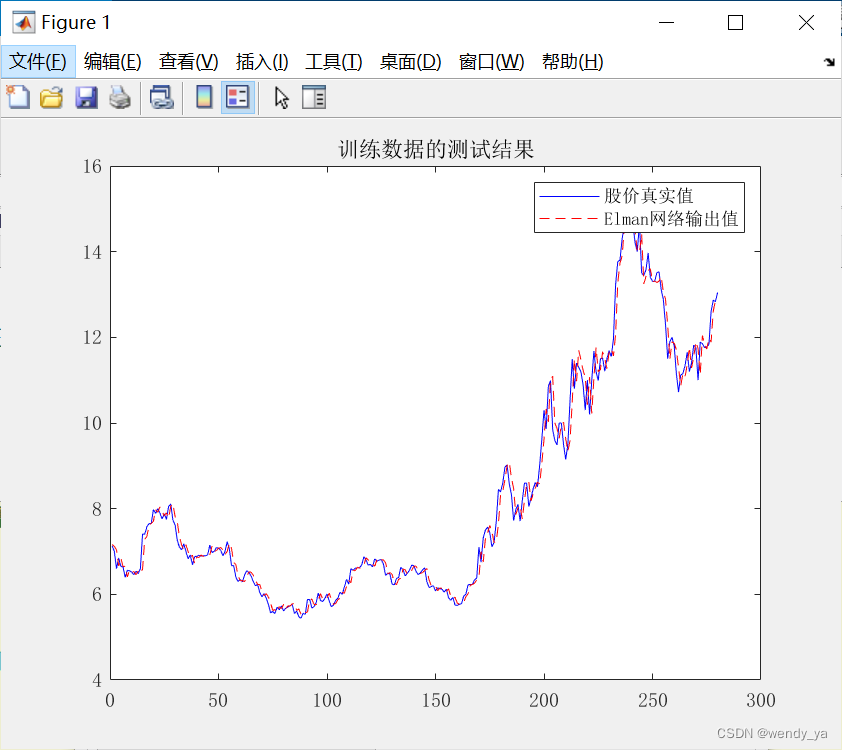
以上便是完整代码了,如果还是不懂,可以下载源码,参考资源:https://download.csdn.net/download/didi_ya/87734622。
制作不易,如果对你有所帮助,记得点个赞哟~