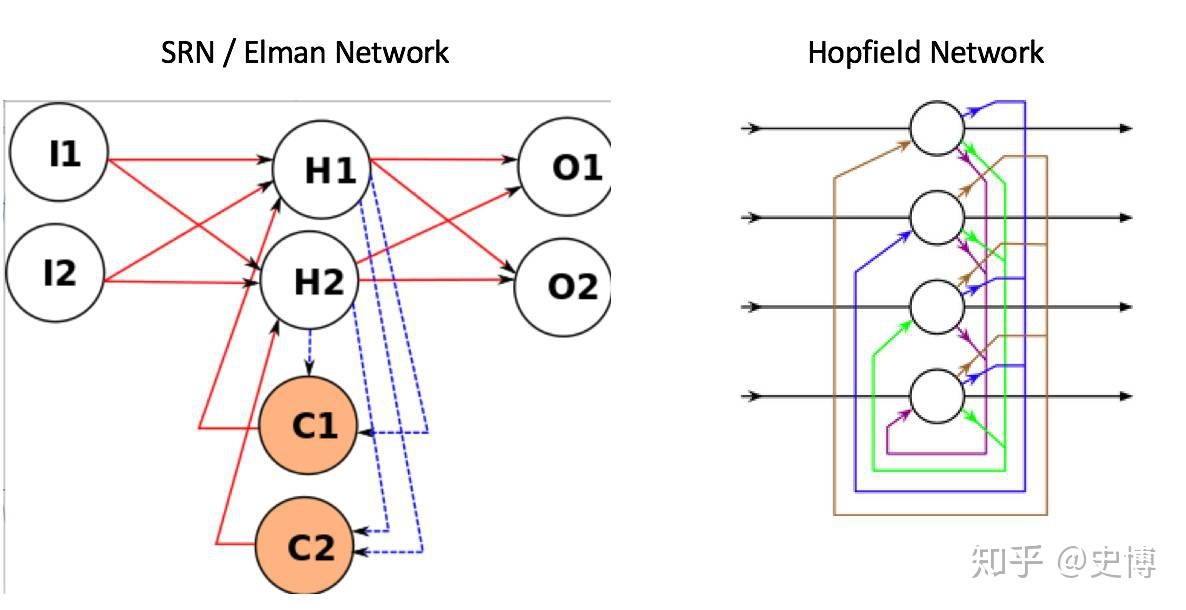
连续Hopfield神经网络
连续Hopfield神经网络(Continuous Hopfield Network, CHN)是一种基于能量最小化原理的神经网络模型,与离散Hopfield网络相比,它的状态是连续的,典型地采用实数值或者概率分布。在优化连续Hopfield神经网络时,需要考虑以下几个方面:
-
选择合适的激活函数:激活函数是神经元的输出与输入之间的非线性映射,对于连续Hopfield网络,常见的激活函数有Sigmoid、Tanh和ReLU等。选择合适的激活函数可以提高网络的性能。
-
设计合适的能量函数:连续Hopfield网络的核心是能量函数,它描述了网络状态的稳定性。设计一个合适的能量函数有助于提高网络的收敛速度和稳定性。
-
权重矩阵初始化:权重矩阵的初始化对网络性能有很大影响,常用的初始化方法包括随机初始化、He初始化和Xavier初始化等。合适的初始化策略可以加快网络的收敛速度并提高性能。
-
学习率调整:学习率是神经网络中的一个重要超参数,它决定了权重更新的速度。采用适当的学习率策略,如固定学习率、衰减学习率或自适应学习率,可以提高优化效果。
-
正则化:正则化是一种防止过拟合的方法,通过在损失函数中添加正则项来实现。常见的正则化方法包括L1正则化、L2正则化和Dropout等。适当的正则化策略可以提高网络的泛化能力。
-
训练策略:对于连续Hopfield网络的训练,可以采用批量梯度下降、随机梯度下降或小批量梯度下降等方法。不同的训练策略对收敛速度和性能有不同的影响,因此需要根据实际问题选择合适的训练方法。
-
模型选择与评估:在训练过程中,可以采用交叉验证、模型选择与超参数调整等技巧,以选出最佳模型和参数设置。此外,还需要合理设计评估指标,以便准确地衡量网络性能。
综上所述,优化连续Hopfield神经网络涉及多个方面的策略和技巧,需要根据实际问题和数据集进行调整,以达到最佳性能。
TSP(旅行商问题,Traveling Salesman Problem)
我们以TSP(旅行商问题,Traveling Salesman Problem)为例,说明如何使用连续Hopfield神经网络进行优化。
TSP问题是一个经典的组合优化问题,要求在给定一组城市和它们之间的距离后,找到一条访问每个城市恰好一次并回到起始城市的最短路径。
在这个例子中,我们可以通过优化连续Hopfield神经网络来求解TSP问题。
-
网络表示:首先,我们需要将TSP问题表示为连续Hopfield神经网络。假设有N个城市,我们可以用一个N×N的矩阵X表示网络状态,其中每个元素x_ij表示城市i在访问顺序中的第j个位置的概率。
-
能量函数:接下来,我们需要设计一个能量函数来度量网络状态的优劣。一个常用的能量函数为:
E(X) = A * (Σ_i(Σ_j x_ij - 1)^2 + Σ_j(Σ_i x_ij - 1)^2) + B * Σ_i Σ_j Σ_k d_ik * x_ij * x_k(j+1)
其中A和B是权衡因子,d_ik是城市i和城市k之间的距离。第一项保证每个城市只被访问一次,第二项保证每个位置只有一个城市,第三项表示总路径长度。
- 动力学方程:为了优化能量函数,我们需要根据能量函数的梯度构造动力学方程。在这个例子中,我们可以采用sigmoid函数作为激活函数,并使用梯度下降法进行优化:
dx_ij/dt = -∂E/∂x_ij + γ * f(x_ij) * (1 - f(x_ij))
其中f(x_ij) = 1/(1 + exp(-β * x_ij)),γ和β是超参数。
-
参数设置与优化:在实际优化过程中,我们需要选择合适的权衡因子A和B,以及超参数γ和β。这些参数可以通过交叉验证或网格搜索等方法进行调整。此外,我们还需要设置合适的学习率和训练策略,例如可以使用自适应学习率和小批量梯度下降法。
-
解码与评估:最后,我们需要将网络状态矩阵X解码为TSP问题的解。常见的解码方法是取每行和每列的最大概率值所对应的城市和位置。然后我们可以计算解的总路径长度,以评估连续Hopfield神经网络求解TSP问题的性能。
通过以上步骤,我们可以使用连续Hopfield神经网络进行TSP问题的优化。
Code
diff_u
% % % % 计算du
function du=diff_u(V,d)
global A D
n=size(V,1);
sum_x=repmat(sum(V,2)-1,1,n);
sum_i=repmat(sum(V,1)-1,n,1);
V_temp=V(:,2:n);
V_temp=[V_temp V(:,1)];
sum_d=d*V_temp;
du=-A*sum_x-A*sum_i-D*sum_d;energy
% % % % % 计算能量函数
function E=energy(V,d)
global A D
n=size(V,1);
sum_x=sumsqr(sum(V,2)-1);
sum_i=sumsqr(sum(V,1)-1);
V_temp=V(:,2:n);
V_temp=[V_temp V(:,1)];
sum_d=d*V_temp;
sum_d=sum(sum(V.*sum_d));
E=0.5*(A*sum_x+A*sum_i+D*sum_d);main
%% 连续Hopfield神经网络的优化—旅行商问题优化计算
%% 清空环境变量、定义全局变量
clear all
clc
global A D
%% 导入城市位置
load city_location
%% 计算相互城市间距离
distance = dist(citys,citys');
%% 初始化网络
N = size(citys,1);
A = 200;
D = 100;
U0 = 0.1;
step = 0.0001;
delta = 2 * rand(N,N) - 1;
U = U0 * log(N-1) + delta;
V = (1 + tansig(U/U0))/2;
iter_num = 10000;
E = zeros(1,iter_num);
%% 寻优迭代
for k = 1:iter_num
% 动态方程计算
dU = diff_u(V,distance);
% 输入神经元状态更新
U = U + dU*step;
% 输出神经元状态更新
V = (1 + tansig(U/U0))/2;
% 能量函数计算
e = energy(V,distance);
E(k) = e;
end
%% 判断路径有效性
[rows,cols] = size(V);
V1 = zeros(rows,cols);
[V_max,V_ind] = max(V);
for j = 1:cols
V1(V_ind(j),j) = 1;
end
C = sum(V1,1);
R = sum(V1,2);
flag = isequal(C,ones(1,N)) & isequal(R',ones(1,N));
%% 结果显示
if flag == 1
% 计算初始路径长度
sort_rand = randperm(N);
citys_rand = citys(sort_rand,:);
Length_init = dist(citys_rand(1,:),citys_rand(end,:)');
for i = 2:size(citys_rand,1)
Length_init = Length_init+dist(citys_rand(i-1,:),citys_rand(i,:)');
end
% 绘制初始路径
figure(1)
plot([citys_rand(:,1);citys_rand(1,1)],[citys_rand(:,2);citys_rand(1,2)],'o-')
for i = 1:length(citys)
text(citys(i,1),citys(i,2),[' ' num2str(i)])
end
text(citys_rand(1,1),citys_rand(1,2),[' 起点' ])
text(citys_rand(end,1),citys_rand(end,2),[' 终点' ])
title(['优化前路径(长度:' num2str(Length_init) ')'])
axis([0 1 0 1])
grid on
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
% 计算最优路径长度
[V1_max,V1_ind] = max(V1);
citys_end = citys(V1_ind,:);
Length_end = dist(citys_end(1,:),citys_end(end,:)');
for i = 2:size(citys_end,1)
Length_end = Length_end+dist(citys_end(i-1,:),citys_end(i,:)');
end
disp('最优路径矩阵');V1
% 绘制最优路径
figure(2)
plot([citys_end(:,1);citys_end(1,1)],...
[citys_end(:,2);citys_end(1,2)],'o-')
for i = 1:length(citys)
text(citys(i,1),citys(i,2),[' ' num2str(i)])
end
text(citys_end(1,1),citys_end(1,2),[' 起点' ])
text(citys_end(end,1),citys_end(end,2),[' 终点' ])
title(['优化后路径(长度:' num2str(Length_end) ')'])
axis([0 1 0 1])
grid on
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
% 绘制能量函数变化曲线
figure(3)
plot(1:iter_num,E);
ylim([0 2000])
title(['能量函数变化曲线(最优能量:' num2str(E(end)) ')']);
xlabel('迭代次数');
ylabel('能量函数');
else
disp('寻优路径无效');
end