| 题目 | 难度 | 备注 |
|---|---|---|
| 2471. 逐层排序二叉树所需的最少操作数目 | 1635 | BFS + 置换环 + 离散化 |
| 2641. 二叉树的堂兄弟节点 II | 1677 | BFS |
文章目录
- 周赛二叉树问题
- [2471. 逐层排序二叉树所需的最少操作数目](https://leetcode.cn/problems/minimum-number-of-operations-to-sort-a-binary-tree-by-level/)
- [2641. 二叉树的堂兄弟节点 II](https://leetcode.cn/problems/cousins-in-binary-tree-ii/)
周赛二叉树问题
2471. 逐层排序二叉树所需的最少操作数目
难度中等27
给你一个 值互不相同 的二叉树的根节点 root 。
在一步操作中,你可以选择 同一层 上任意两个节点,交换这两个节点的值。
返回每一层按 严格递增顺序 排序所需的最少操作数目。
节点的 层数 是该节点和根节点之间的路径的边数。
示例 1 :
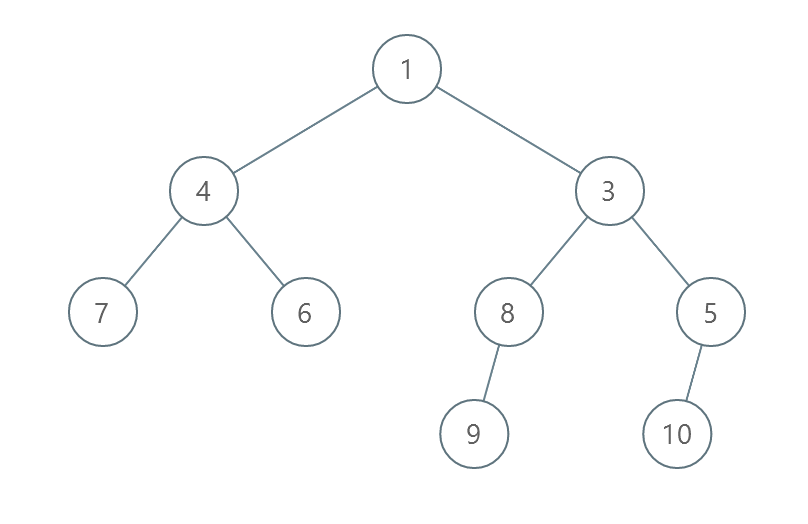
输入:root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出:3
解释:
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作,所以返回 3 。
可以证明 3 是需要的最少操作数目。
示例 2 :
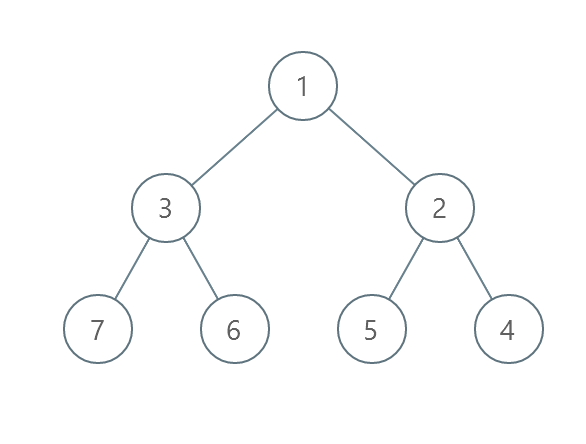
输入:root = [1,3,2,7,6,5,4]
输出:3
解释:
- 交换 3 和 2 。第 2 层变为 [2,3] 。
- 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。
- 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
共计用了 3 步操作,所以返回 3 。
可以证明 3 是需要的最少操作数目。
提示:
- 树中节点的数目在范围
[1, 105]。 1 <= Node.val <= 105- 树中的所有值 互不相同 。
题解:https://leetcode.cn/problems/minimum-number-of-operations-to-sort-a-binary-tree-by-level/solution/by-liu-wan-qing-zjlj/
以计算使得 [7, 6, 8, 5] 严格递增需要的最小交换次数为例,画出置换环算法图解如下:
经典问题:置换环求解数组排序需要的最小交换次数
置换环的思想为 : 对每个节点,将其指向其排序后应该放到的位置,直到首位相接形成了一个环。
具体实现思想:
- 使用 Map 哈希表记录每个节点值以及其应该放到的位置
- 从头到尾遍历初始数组,使用
flag[]数组标记当前元素是否已经参与过(即已经被加入环中),对已经参与过的数组则不再需要遍历。每次成环结束,记录成环个数 loop。 - 最终最小交换次数为 :数组长度 - 成环个数(
nums.size() - loop)
置换环算法一般情况代码如下:
// 返回使得 nums 递增需要的最小交换元素次数
public int minChanges(int[] nums){
int[] copy = Arrays.copyOf(nums, nums.length);
Arrays.sort(copy); // 排序,获得有序的nums数组copy
// 离散化:记录元素原本应该出现的位置 i
HashMap<Integer, Integer> map = new HashMap<>();
for(int i=0; i<copy.length; i++){
map.put(copy[i], i);
}
boolean[] flag = new boolean[nums.length]; // 用于标记 nums[i] 是否已经被加入环中
int loop = 0; // 环的个数
for(int i=0; i<nums.length; i++){
if(!flag[i]){
int j = i;
while(!flag[j]){ // 画环
int index = map.get(nums[j]); // 当前节点指向的实际存放位置,画环过程
flag[j] = true; // 将 j 加入环中
j = index; // 将当前节点移动到环上下个节点
}
loop++; // 环数递增
}
}
return nums.length - loop; // 最小交换次数为 : 数组长度 - 环数
}
代码实现
class Solution {
public int minimumOperations(TreeNode root) {
int res = 0;
if(root == null) return res;
Deque<TreeNode> dq = new ArrayDeque<>();
dq.add(root);
while(!dq.isEmpty()){
List<Integer> levellist = new ArrayList<>();
int size = dq.size();
while(size-- > 0){
TreeNode node = dq.poll();
levellist.add(node.val);
if(node.left != null) dq.add(node.left);
if(node.right != null) dq.add(node.right);
}
// 计算该数组排序需要的最小交换次数:置换环
int loop = 0;
List<Integer> tmp = new ArrayList<>(levellist);
Collections.sort(levellist);
boolean[] flag = new boolean[tmp.size()];
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < tmp.size(); i++){
map.put(levellist.get(i), i);
}
for(int i = 0; i < tmp.size(); i++){
if(!flag[i]){
int j = i;
while(!flag[j]){
int index = map.get(tmp.get(j));
flag[j] = true;
j = index;
}
loop++;
}
}
res += (tmp.size() - loop);
}
return res;
}
}
2641. 二叉树的堂兄弟节点 II
难度中等0
给你一棵二叉树的根 root ,请你将每个节点的值替换成该节点的所有 堂兄弟节点值的和 。
如果两个节点在树中有相同的深度且它们的父节点不同,那么它们互为 堂兄弟 。
请你返回修改值之后,树的根 root 。
注意,一个节点的深度指的是从树根节点到这个节点经过的边数。
示例 1:
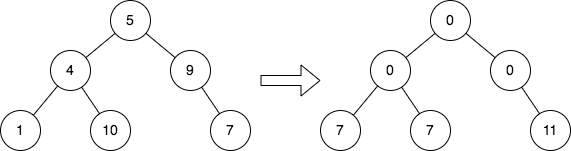
输入:root = [5,4,9,1,10,null,7]
输出:[0,0,0,7,7,null,11]
解释:上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
- 值为 5 的节点没有堂兄弟,所以值修改为 0 。
- 值为 4 的节点没有堂兄弟,所以值修改为 0 。
- 值为 9 的节点没有堂兄弟,所以值修改为 0 。
- 值为 1 的节点有一个堂兄弟,值为 7 ,所以值修改为 7 。
- 值为 10 的节点有一个堂兄弟,值为 7 ,所以值修改为 7 。
- 值为 7 的节点有两个堂兄弟,值分别为 1 和 10 ,所以值修改为 11 。
示例 2:

输入:root = [3,1,2]
输出:[0,0,0]
解释:上图展示了初始的二叉树和修改每个节点的值之后的二叉树。
- 值为 3 的节点没有堂兄弟,所以值修改为 0 。
- 值为 1 的节点没有堂兄弟,所以值修改为 0 。
- 值为 2 的节点没有堂兄弟,所以值修改为 0 。
提示:
- 树中节点数目的范围是
[1, 105]。 1 <= Node.val <= 104
BFS遍历
https://leetcode.cn/problems/cousins-in-binary-tree-ii/solution/bfssuan-liang-ci-pythonjavacgo-by-endles-b72a/
站在父节点的视角,去看下一层节点的取值:(站在父节点的位置上解决子节点的问题)!!!启发点:对于一个节点 x 来说,它的所有堂兄弟节点值的和,等价于 x 这层的所有节点值之和,减去 x 及其兄弟节点的值之和
BFS层序遍历二叉树,对于每一层:
首先,遍历当前层的每个节点,通过节点的左右儿子,计算下层的节点值之和 nextLevelSum;
然后,再次遍历当前层的每个节点 x,计算 x 的左右儿子的节点值之和 childrenSum,更新 x 的左右儿子的节点值为nextLevelSum - childrenSum。
class Solution {
public TreeNode replaceValueInTree(TreeNode root) {
root.val = 0;
// 使用List和临时变量tmp来模拟队列(Deque没有get方法)
List<TreeNode> q = new ArrayList<>();
q.add(root);
while(!q.isEmpty()){
// 用临时遍历保存本层节点,后面需要计算本层节点x左右儿子的节点值之和
List<TreeNode> tmp = q;
q = new ArrayList<>();
int nextLevelSum = 0; // 下一层的节点之和
// 获取下层节点和的同时进行BFS操作
for(TreeNode node : tmp){
if(node.left != null){
q.add(node.left);
nextLevelSum += node.left.val;
}
if(node.right != null){
q.add(node.right);
nextLevelSum += node.right.val;
}
}
// 再次遍历,更新下一层的节点值
for(TreeNode node : tmp){
int childSum = (node.left != null ? node.left.val : 0) +
(node.right != null ? node.right.val : 0);
if(node.left != null) node.left.val = nextLevelSum - childSum;
if(node.right != null) node.right.val = nextLevelSum - childSum;
}
}
return root;
}
}