背包问题题型

• 等和子集 —0-1背包能否装满
• 最后一块石头—0-1背包尽量装满
• 目标和—0-1背包装满，且有多少种装的方式（组合问题）

1049. 最后一块石头的重量 II

• 题目链接：代码随想录

• 解题思路：

  本题是尽量凑成重量相同的两堆，然后进行碰撞

public int lastStoneWeightII(int[] stones) {
    //定义dp数组，dp数组是重量的背包
    //dp[i]表示重量为i的背包能放下最大容量的石头
    int[] dp = new int[1501];

    //sum[i]既表示重量也表示价值
    int sum = 0;
    for (int stone : stones) {
        sum += stone;
    }

    int target = sum / 2;

    for(int i = 0; i < stones.length; i++) {//表示石头
        for(int j = target;j >= stones[i];j--){//表示背包重量
            dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
        }
    }

    //和上一题处理唯一不同的地方
    //半和target最多能装满的的价值
    //(sum - dp[target])表示剩下的价值，一定比dp[target]大，因为target向下取整
    return (sum - dp[target]) - dp[target];
}

494. 目标和

• 题目链接：代码随想录

求组合类问题的0-1背包问题都是dp[j] += dp[j - nums[i]]

• 解题思路：
  1.dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法
  2.dp[j] += dp[j - nums[i]]
  3.初始化： dp[0] 为 1
  4.遍历顺序：从后向前遍历

• 图像理解：

  1.left部分和的推导

  

  2.递归公式的推导

  

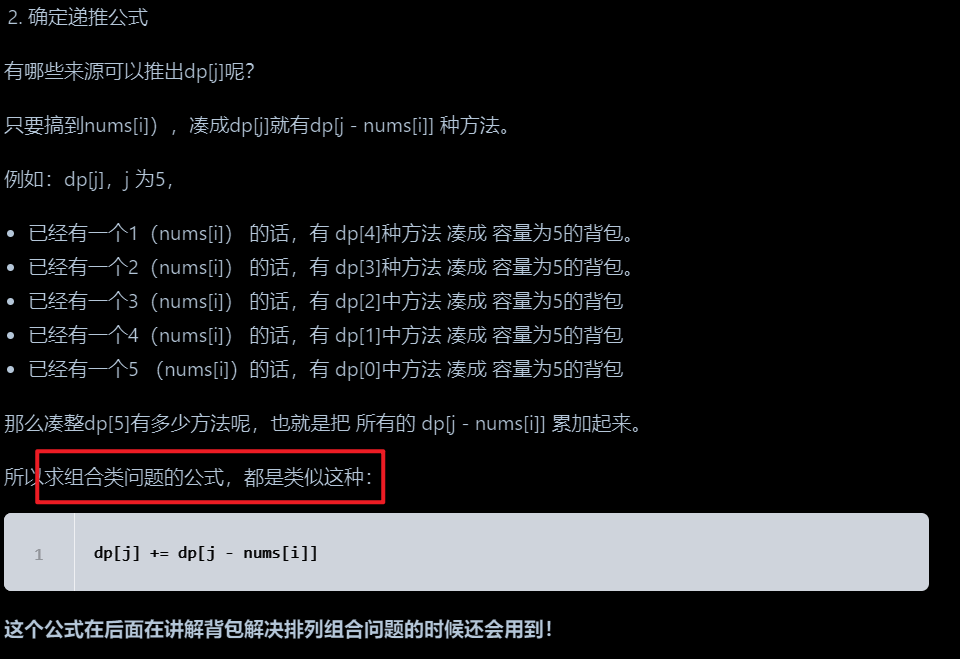
  3.过程

  

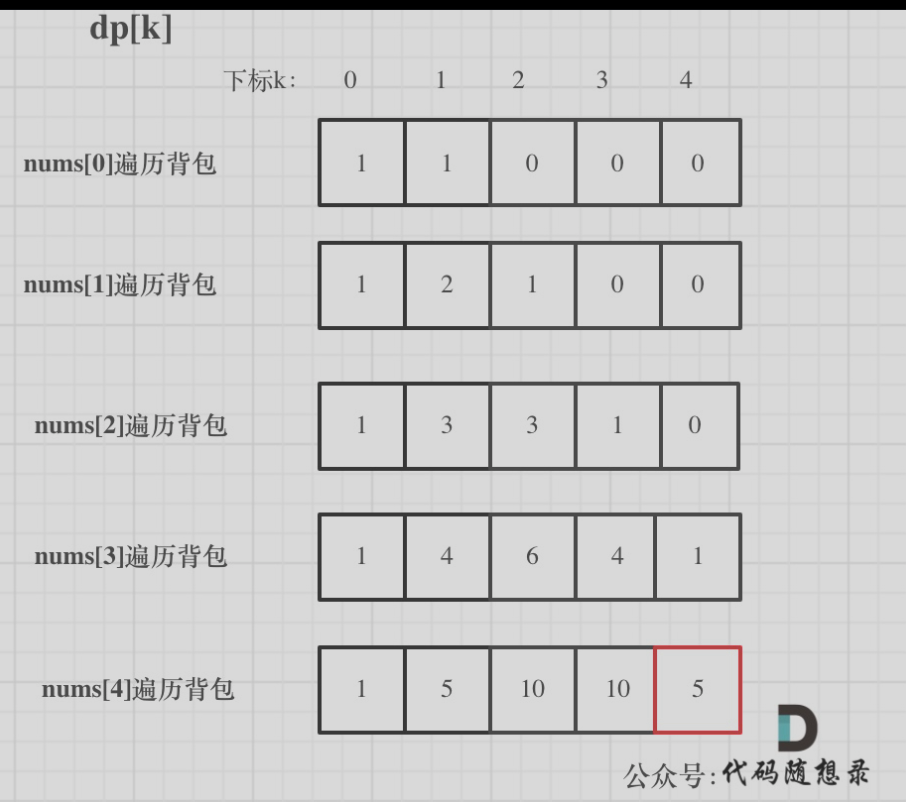
public int findTargetSumWays(int[] nums, int target) {
    int sum = 0;
    for (int i = 0; i < nums.length; i++) sum += nums[i];

    //防止target目标过大
    if ( target < 0 && sum < -target) return 0;

    //没有组合的情况
    if ((target + sum) % 2 != 0) return 0;

    int size = (target + sum) / 2;//左边集合的应该有的值
    if(size < 0) size = -size;

    int[] dp = new int[size + 1];
    dp[0] = 1;

    for (int i = 0; i < nums.length; i++) {
        for (int j = size; j >= nums[i]; j--) {
            dp[j] += dp[j - nums[i]];
        }
    }
    return dp[size];
}

474.一和零

• 题目链接[代码随想录]