前言

本文介绍了算法实验排序中减治法的程序设计。减治法是一种常用的算法设计技术，它通过减少问题的规模来求解问题。减治法可以应用于排序问题，例如插入排序、选择排序和快速排序等。本文将分析这些排序算法的原理、实现和性能，并给出相应的程序代码和测试结果。

本文中使用的语言是C语言，使用的工具是devc++

实验内容

给出一个记录序列，用堆排序的方法将其进行升序排列，输出结果，输出时要求有文字说明。请任选一种语言编写程序实现上述算法，并分析其算法复杂度。

实验目的

（1）掌握堆的有关概念；

（2）掌握堆排序的基本思想和其算法的实现过程；

（3）熟练掌握筛选算法的实现过程；

（4）在掌握的基础上编程实现堆排序的具体实现过程。

实验分析

这个题目要求使用堆排序的方法将一个记录序列进行升序排列，并输出结果和文字说明。需要选择一种编程语言来实现堆排序算法，并分析其算法复杂度。这个题目考察了对堆排序算法的理解和应用能力，以及你对编程语言的掌握程度和代码风格的规范性。需要注意以下几点：

堆排序算法是一种基于二叉堆结构的排序方法，它利用了二叉堆的性质，即堆顶元素是最大或最小值，来不断地选出序列中的最大或最小值，并将其放在正确的位置。它分为两个步骤：构建堆和调整堆。构建堆是从最后一个非叶子节点开始，自下而上地调整每个节点，使其满足大顶堆或小顶堆的性质。调整堆是从最后一个元素开始，将堆顶元素与末尾元素交换，然后调整剩余的元素为新的堆，重复这个过程直到只剩一个元素。
堆排序算法的时间复杂度为O(nlogn)，空间复杂度为O(1)。它是一种原地排序算法，不需要额外的空间来存储数据。它的时间复杂度是由构建堆和调整堆的次数决定的，每次构建或调整堆都需要O(logn)的时间，而总共需要进行n次构建或调整，所以总的时间复杂度为O(nlogn)。它的空间复杂度是由交换元素所需的辅助空间决定的，每次交换只需要一个临时变量来存储数据，所以总的空间复杂度为O(1)。

实验过程

流程演示

首先，我们从最后一个非叶子节点开始，自下而上构建大顶堆。最后一个非叶子节点的索引是(n/2-1)，其中n是序列的长度。在这个例子中，n=9，所以最后一个非叶子节点的索引是3，对应的元素是6。我们从这个节点开始，依次向上调整每个节点，使其满足大顶堆的性质。调整的过程是：比较当前节点和它的左右孩子，如果当前节点小于它的左右孩子中的任何一个，就交换它们，并递归地调整被交换的子树。调整后的结果如下：

        9
      /   \
     8     7
    / \   / \
   6   5 4   3
  / \
 2   1

然后，我们将堆顶元素与末尾元素交换，即将9和1交换，这样我们就得到了序列中的最大值，并将其放在了正确的位置。交换后，我们将剩余的元素（除了最后一个）看作一个新的堆，并对其进行调整，使其满足大顶堆的性质。调整后的结果如下：

        8
      /   \
     6     7
    / \   / \
   2   5 4   3
 /
1

接着，我们重复上面的步骤，将堆顶元素与末尾元素交换，即将8和2交换，这样我们就得到了序列中的第二大值，并将其放在了正确的位置。交换后，我们将剩余的元素（除了最后两个）看作一个新的堆，并对其进行调整，使其满足大顶堆的性质。调整后的结果如下：

我们继续重复上面的步骤，直到只剩一个元素为止。每次交换和调整后，我们都会得到序列中的一个最大值，并将其放在了正确的位置。最终，我们得到了升序排列的序列[1, 2, 3, 4, 5, 6, 7, 8, 9]

写出伪代码

//定义一个交换函数，接受一个数组和两个索引作为参数，交换这两个索引对应的元素
swap(arr, i, j):
  temp <- arr[i]
  arr[i] <- arr[j]
  arr[j] <- temp

//定义一个调整函数，接受一个数组，一个数组的长度，和一个需要调整的节点的索引作为参数，调整该节点和它的子树，使其满足大顶堆的性质
heapify(arr, n, i):
  largest <- i //假设当前节点为最大值
  left <- 2 * i + 1 //左孩子的索引
  right <- 2 * i + 2 //右孩子的索引
  //如果左孩子存在且大于当前节点，更新最大值的索引
  if left < n and arr[left] > arr[largest]:
    largest <- left
  //如果右孩子存在且大于当前节点，更新最大值的索引
  if right < n and arr[right] > arr[largest]:
    largest <- right
  //如果最大值不是当前节点，交换它们，并递归地调整被交换的子树
  if largest != i:
    swap(arr, i, largest)
    heapify(arr, n, largest)

//定义一个堆排序函数，接受一个数组和一个数组的长度作为参数，对该数组进行升序排列
heapSort(arr, n):
  //从最后一个非叶子节点开始，自下而上地构建大顶堆
  for i from n / 2 - 1 to 0:
    heapify(arr, n, i)
  //从最后一个元素开始，将堆顶元素与末尾元素交换，然后调整剩余的元素为新的大顶堆，重复这个过程直到只剩一个元素
  for i from n - 1 to 1:
    swap(arr, 0, i)
    heapify(arr, i, 0)

//定义一个打印函数，接受一个数组和一个数组的长度作为参数，打印该数组中的每个元素
printArray(arr, n):
  for i from 0 to n - 1:
    print arr[i] and a space
  print a newline

//测试代码
main():
  //通过键盘输入序列的长度和元素
  print "请输入序列的长度："
  read n //读取序列的长度
  print "请输入序列的元素："
  arr <- an array of size n //动态分配内存空间存储序列
  for i from 0 to n - 1:
    read arr[i] //读取每个元素
  
  //输出原始序列
  print "原始序列："
  printArray(arr, n)
  
  //使用堆排序算法对序列进行升序排列
  heapSort(arr, n)
  
  //输出排序结果
  print "排序结果："
  printArray(arr, n)

实验代码

#include <stdio.h>
#include <stdlib.h>

//交换数组中的两个元素
void swap(int arr[], int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

//调整数组中的元素，使其满足大顶堆的性质
void heapify(int arr[], int n, int i) {
    int largest = i; //假设当前节点为最大值
    int left = 2 * i + 1; //左孩子的索引
    int right = 2 * i + 2; //右孩子的索引
    //如果左孩子存在且大于当前节点，更新最大值的索引
    if (left < n && arr[left] > arr[largest]) {
        largest = left;
    }
    //如果右孩子存在且大于当前节点，更新最大值的索引
    if (right < n && arr[right] > arr[largest]) {
        largest = right;
    }
    //如果最大值不是当前节点，交换它们，并递归调整被交换的子树
    if (largest != i) {
        swap(arr, i, largest);
        heapify(arr, n, largest);
    }
}

//堆排序算法
void heapSort(int arr[], int n) {
    //从最后一个非叶子节点开始，自下而上构建大顶堆
    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(arr, n, i);
    }
    //从最后一个元素开始，将堆顶元素与末尾元素交换，然后调整剩余的元素为新的大顶堆，重复这个过程直到只剩一个元素
    for (int i = n - 1; i > 0; i--) {
        swap(arr, 0, i);
        heapify(arr, i, 0);
    }
}

//打印数组
void printArray(int arr[], int n) {
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

//测试代码
int main() {
    //通过键盘输入序列的长度和元素
    printf("请输入序列的长度：\n");
    int n;
    scanf("%d", &n); //读取序列的长度
    printf("请输入序列的元素：\n");
    int *arr = (int *)malloc(sizeof(int) * n); //动态分配内存空间存储序列
    for (int i = 0; i < n; i++) {
        scanf("%d", &arr[i]); //读取每个元素
    }
    
    //输出原始序列
    printf("原始序列：\n");
    printArray(arr, n);
    
    //使用堆排序算法对序列进行升序排列
    heapSort(arr, n);
    
    //输出排序结果
    printf("排序结果：\n");
    printArray(arr, n);
    
    //释放内存空间
    free(arr);
    
    return 0;
}

代码详解

代码分为以下几个部分：

交换数组中的两个元素的函数swap，它接受一个数组和两个索引作为参数，然后将这两个索引对应的元素互换位置。
调整数组中的元素，使其满足大顶堆的性质的函数heapify，它接受一个数组，一个数组的长度，和一个需要调整的节点的索引作为参数。它首先假设当前节点为最大值，然后比较它和它的左右孩子，如果左右孩子中有比它大的，就更新最大值的索引。如果最大值不是当前节点，就交换它们，并递归地调整被交换的子树。
堆排序算法的函数heapSort，它接受一个数组和一个数组的长度作为参数。它首先从最后一个非叶子节点开始，自下而上构建大顶堆。然后从最后一个元素开始，将堆顶元素与末尾元素交换，然后调整剩余的元素为新的大顶堆，重复这个过程直到只剩一个元素。
打印数组的函数printArray，它接受一个数组和一个数组的长度作为参数。它遍历数组中的每个元素，并打印出来。
测试代码的主函数main，它定义了一个待排序的序列，并调用了heapSort函数对其进行排序，并打印了排序前后的结果。

运行结果

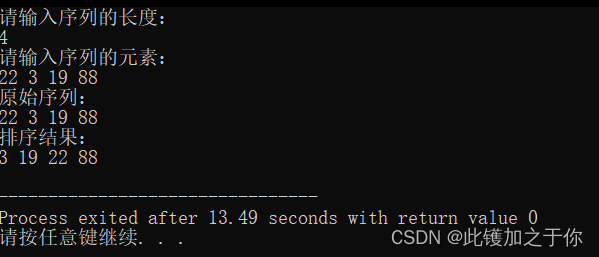
总结

减治法是一种算法设计策略，它的基本思想是将一个规模为n的问题转化为一个规模为n-1的子问题，然后利用子问题的解来求解原问题。减治法可以分为三种类型，分别是减去一个常量、减去一个常数因子和减去一个可变因子。在排序问题中，减治法有很多应用，例如插入排序、堆排序等。

插入排序是一种基于减一法的排序算法，它的过程类似于扑克牌抓牌时的排序。每次从未排序的序列中取出一个元素，将其插入到已排序的序列中合适的位置，使得已排序的序列仍然有序。插入排序的时间复杂度为O(n^2)，空间复杂度为O(1)。插入排序是一种稳定的排序算法，也就是说，相同元素的相对顺序不会改变。

堆排序是一种基于减去常数因子的排序算法，它的过程利用了堆这种数据结构。堆是一种特殊的完全二叉树，它满足堆序性质，即每个节点的值都不小于（或不大于）其子节点的值。堆可以分为最大堆和最小堆，分别用于降序和升序排列。堆排序的过程分为两个步骤：建堆和调整堆。建堆是将一个无序的数组构造成一个堆，调整堆是每次将堆顶元素与最后一个元素交换，并将剩余的元素重新调整成一个堆，直到只剩下一个元素。堆排序的时间复杂度为O(nlogn)，空间复杂度为O(1)。堆排序是一种不稳定的排序算法，也就是说，相同元素的相对顺序可能会改变。