1.问题简介

多臂老虎机问题可以被看作简化版的强化学习问题，算是最简单的“和环境交互中的学习”的一种形式，不存在状态信息，只有动作和奖励。多臂老虎机中的探索与利用（exploration vs. exploitation）问题一直以来都是一个特别经典的问题，理解它能够帮助我们学习强化学习。

2.问题介绍

2.1问题定义

在多臂老虎机（multi-armed bandit，MAB）问题中，有一个拥有 K根拉杆的老虎机，拉动每一根拉杆都对应一个关于奖励的概率分布R。我们每次拉动其中一根拉杆，就可以从该拉杆对应的奖励概率分布中获得一个奖励。我们在各根拉杆的奖励概率分布未知的情况下，从头开始尝试，目标是在操作 T次拉杆后获得尽可能高的累积奖励。由于奖励的概率分布是未知的，因此我们需要在“探索拉杆的获奖概率”和“根据经验选择获奖最多的拉杆”中进行权衡。

2.2形式化描述

多臂老虎机问题可以表示为一个元组 $\left \langle A,R \right \rangle$ ，其中：

A为动作集合，其中一个动作表示拉动一个拉杆。若多臂老虎机一共有K根拉杆，那动作空间就是集合 $\left \{ a_{1},\cdots a_{i},\cdots ,a_{k}\right \}$ ，我们用 $a_{t}\ni A$ 表示任意一个动作；
R为奖励概率分布，拉动每一根拉杆的动作a都对应一个奖励概率分布R(r|a)，拉动不同拉杆的奖励分布通常是不同的。

假设每个时间步只能拉动一个拉杆，多臂老虎机的目标为最大化一段时间步T内累积的奖励: $max\sum_{t=1}^{T}r_{i},r_{i}~R(\cdot |a_{t})$

其中 $a_{t}$ 表示在第t时间步拉动某一拉杆的动作， $r_{t}$ 表示动作 $a_{t}$ 获得的奖励。

对于每一个动作a，定义其期望奖励为:

于是，至少存在一根拉杆，它的期望奖励不小于拉动其他任意一根拉杆，我们将该最优期望奖励表示为:

懊悔(regret)定义为拉动当前拉杆的动作a与最优拉杆的期望奖励差，即 :

$R(a)=Q^{*}-Q(a)$

累积懊悔（cumulative regret）即操作 T次拉杆后累积的懊悔总量，对于一次完整的T步决策 $\left \{ a_{1},a_{2},\cdots ,a_{T} \right \}$ ，累积懊悔为：

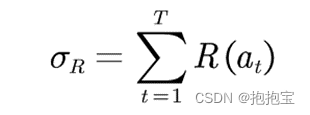
MAB 问题的目标为最大化累积奖励，等价于最小化累积懊悔。

为了知道拉动哪一根拉杆能获得更高的奖励，我们需要估计拉动这根拉杆的期望奖励。由于只拉动一次拉杆获得的奖励存在随机性，所以需要多次拉动一根拉杆，然后计算得到的多次奖励的期望，其算法流程如下所示：

以上 for 循环中的第四步如此更新估值，是因为这样可以进行增量式的期望更新，为什么不按照常规方法将所有数求和再除以次数呢？具体原因如下：

因为如果将所有数求和再除以次数，其缺点是每次更新的时间复杂度和空间复杂度均为 O(n)。而采用增量式更新，时间复杂度和空间复杂度均为O(1) 。

3. 代码实现

以下代码来实现一个拉杆数为 10 的多臂老虎机。其中拉动每根拉杆的奖励服从伯努利分布（Bernoulli distribution），即每次拉下拉杆有P的概率获得的奖励为 1，有1-P的概率获得的奖励为 0。奖励为 1 代表获奖，奖励为 0 代表没有获奖。

# 导入需要使用的库,其中numpy是支持数组和矩阵运算的科学计算库,而matplotlib是绘图库
import numpy as np
import matplotlib.pyplot as plt


class BernoulliBandit:
    """ 伯努利多臂老虎机,输入K表示拉杆个数 """
    def __init__(self, K):
        self.probs = np.random.uniform(size=K)  # 随机生成K个0～1的数,作为拉动每根拉杆的获奖
        # 概率
        self.best_idx = np.argmax(self.probs)  # 获奖概率最大的拉杆
        self.best_prob = self.probs[self.best_idx]  # 最大的获奖概率
        self.K = K

    def step(self, k):
        # 当玩家选择了k号拉杆后,根据拉动该老虎机的k号拉杆获得奖励的概率返回1（获奖）或0（未
        # 获奖）
        if np.random.rand() < self.probs[k]:
            return 1
        else:
            return 0


np.random.seed(1)  # 设定随机种子,使实验具有可重复性
K = 10
bandit_10_arm = BernoulliBandit(K)
print("随机生成了一个%d臂伯努利老虎机" % K)
print("获奖概率最大的拉杆为%d号,其获奖概率为%.4f" %
      (bandit_10_arm.best_idx, bandit_10_arm.best_prob))

接下来我们用一个 Solver 基础类来实现上述的多臂老虎机的求解方案。需要实现下列函数功能：根据策略选择动作、根据动作获取奖励、更新期望奖励估值、更新累积懊悔和计数。在下面的 MAB 算法基本框架中，我们将根据策略选择动作、根据动作获取奖励和更新期望奖励估值放在 run_one_step() 函数中，由每个继承 Solver 类的策略具体实现。而更新累积懊悔和计数则直接放在主循环 run() 中。

class Solver:
    """ 多臂老虎机算法基本框架 """
    def __init__(self, bandit):
        self.bandit = bandit
        self.counts = np.zeros(self.bandit.K)  # 每根拉杆的尝试次数
        self.regret = 0.  # 当前步的累积懊悔
        self.actions = []  # 维护一个列表,记录每一步的动作
        self.regrets = []  # 维护一个列表,记录每一步的累积懊悔

    def update_regret(self, k):
        # 计算累积懊悔并保存,k为本次动作选择的拉杆的编号
        self.regret += self.bandit.best_prob - self.bandit.probs[k]
        self.regrets.append(self.regret)

    def run_one_step(self):
        # 返回当前动作选择哪一根拉杆,由每个具体的策略实现
        raise NotImplementedError

    def run(self, num_steps):
        # 运行一定次数,num_steps为总运行次数
        for _ in range(num_steps):
            k = self.run_one_step()
            self.counts[k] += 1
            self.actions.append(k)
            self.update_regret(k)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/464561.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！