题目

请根据二叉树的前序遍历，中序遍历恢复二叉树，并打印出二叉树的右视图

数据范围： 0≤n≤10000
要求： 空间复杂度 O(n)，时间复杂度 O(n)

如输入[1,2,4,5,3],[4,2,5,1,3]时，通过前序遍历的结果[1,2,4,5,3]和中序遍历的结果[4,2,5,1,3]可重建出以下二叉树：

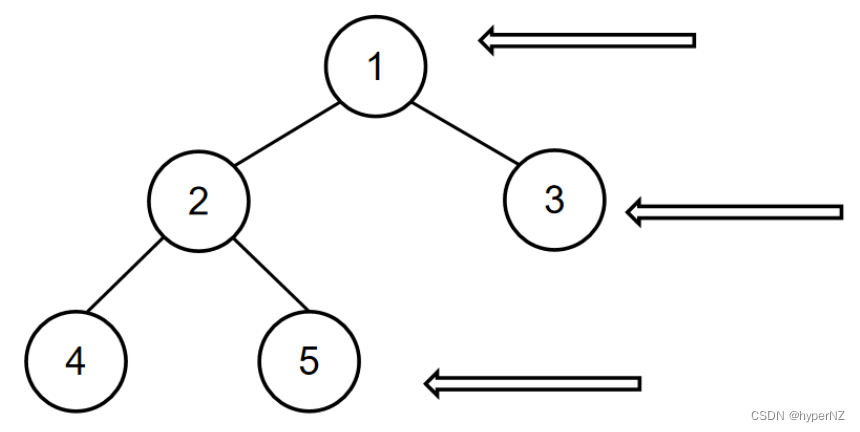
所以对应的输出为[1,3,5]。

示例1

输入：[1,2,4,5,3],[4,2,5,1,3]

返回值：[1,3,5]

备注：二叉树每个节点的值在区间[1,10000]内，且保证每个节点的值互不相同。

---

思路：BM40 + 层序遍历

• 利用BM40的做法根据二叉树的前序遍历，中序遍历恢复二叉树。
• 二叉树的右视图就是二叉树每一层的最后一个节点的集合。
• 故层序遍历，并将当前层的最后一个节点记录下，即为所求。

语法：Integer类型的List转为int[]数组：使用stream

List list = new ArrayList<>();
int[] arr = list.stream().mapToInt(Integer::valueOf).toArray();

---

代码

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 求二叉树的右视图
     * @param xianxu int整型一维数组 先序遍历
     * @param zhongxu int整型一维数组 中序遍历
     * @return int整型一维数组
     */
    public int[] solve (int[] xianxu, int[] zhongxu) {//输出右视图
        TreeNode root = BuildTree(xianxu, zhongxu);
        List<Integer> res = new ArrayList<Integer>();//收集结果
        //边界条件
        if (root.left == null && root.right == null) {
            res.add(root.val);
            return res.stream().mapToInt(Integer::valueOf).toArray();
        }

        //层序遍历
        Queue<TreeNode> que = new LinkedList<TreeNode>();
        que.offer(root);
        while (!que.isEmpty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode cur = que.poll();
                if (cur.left != null) {
                    que.add(cur.left);
                }
                if (cur.right != null) {
                    que.add(cur.right);
                }
                if (i == size - 1) {
                    res.add(cur.val);
                }
            }
        }
        return res.stream().mapToInt(Integer::valueOf).toArray();
    }

    public static TreeNode BuildTree(int[] pre, int[] vin) {//重建二叉树
        if (pre.length == 0 || vin.length == 0) {
            return null;
        }
        if (pre.length == 1 && vin.length == 1 && pre[0] == vin[0]) {
            return new TreeNode(pre[0]);
        }

        TreeNode root = new TreeNode(pre[0]);
        int n = pre.length;
        //在中序序列中找根，递归构建左右子树
        for (int i = 0; i < n; i++) {
            if (vin[i] == pre[0]) {
                root.left = BuildTree(Arrays.copyOfRange(pre, 1, i + 1), Arrays.copyOfRange(vin, 0, i));
                root.right = BuildTree(Arrays.copyOfRange(pre, i + 1, n), Arrays.copyOfRange(vin, i + 1, n));
                break;
            }
        }
        return root;
    }
}