根据已经有数据进行预测的研究方法有很多,包括arima模型、指数平滑法、灰色预测等,本文针对马尔可夫预测进行阐述。比如研究中国移动,中国联通和中国电信三家运营商,他们的用户可以互相携号转网,已经当前3家运营商的市场份额,而且也能测试出用户转网的可能性,那么将来3家运营商的市场份额情况如何,即利用当前已知的两项数据,分别是当前的市场份额、用户接下来使用运营商的可能性(即转移概率矩阵),则可预测将来3家运营商的市场份额情况。
上述中提及‘3家运营商’,马尔可夫预测模型中称其为‘3种状态’。另3家运营商的当前市场份额情况,专业术语称为‘初始概率值’,即最初情况下运营商的市场份额情况,类似下图中3家运营商的市场份额分别是55%,25%和20%。
另外,接下来(比如明年)用户使用运营商的可能性,比如下图中移动用户明年还是使用移动的可能性是0.8,移动用户使用电信的可能性是0.15,移动用户使用联通的可能性是0.05,当然还有类似电信或者联通用户,接下来选择运营商的各个概率情况,3家运营商组成3*3的转移概率矩阵。
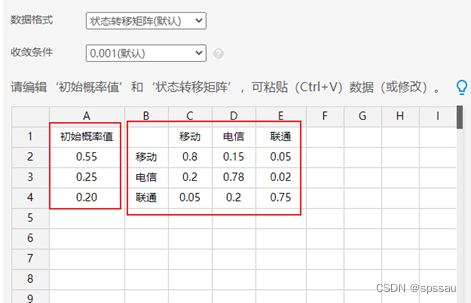
马尔可夫预测案例
背景
当前3家运营商分别的市场占比为0.55,0.25和0.2,但是有携号转网政策后,用户可自由的切换运营商,当前从调查数据中可得到,移动用户预期下年还会使用移动的比例是80%,使用电信的比例是15%,联通的比例是5%。电信用户接下来会使用移动的比例是20%,继续使用电信的比例是78%,使用联通的比例是2%。联通用户接下来使用移动的比例是5%,电信为20%,继续使用联通的比例是75%。现希望预期后续比如10年后,3家运营商的市场份额情况如何。
结合3家公司当前的市场份额即‘初始概率值’,以及3家公司分别的转移概率即‘状态转移矩阵’,将数据录入到SPSSAU中,如下图所示:
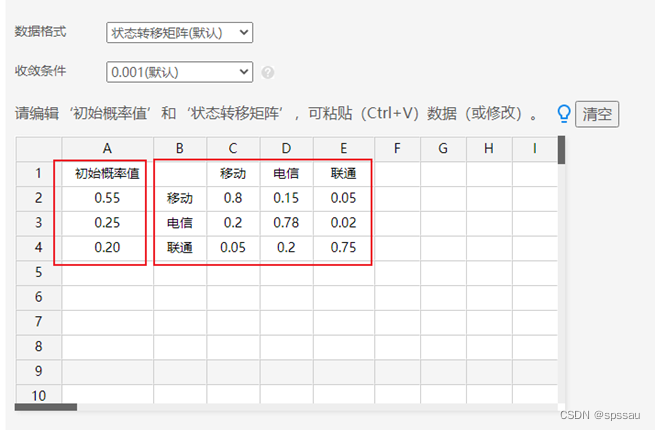
理论
马尔可夫预测涉及3个术语名词,如下说明:
| 术语 | 说明 |
| 状态 | 比如3家运营商,当前使用某运营(比如当前使用联通)就是一种状态 |
| 初始概率值 | 比如当前3家运营商分别的市场占有率情况 |
| 状态转移矩阵 | 预期接下来的3种状态的来回转移可能性,组成的数学矩阵 |
马尔可夫预测的理论在于,利用当前概率值,以及接下来的转移概率,比如当年3家运营商的市场占比比,下1周期(比如明年)运营商使用的转移概率。计算明年后的市场占比,并且再基于‘明年的市场占比’作为‘初始概率值’,接着计算后年的市场占比等,一直循环下去。那么什么时候结束呢,即何时达到市场均衡呢,此时就靠‘收敛条件’这个参数来控制,系统默认是0.001,即误差小于千分之1(即来回变化不会高于千分之1时),此时模型停止计算。
特别提示:
- SPSSAU支持两种数据格式,分别是‘状态转移矩阵’和‘状态数据’。‘状态转移矩阵’要求提供‘初始概率值’和‘状态转移矩阵’。如果是‘状态数据’则需要提供‘初始概率值’和‘原始状态数据’,系统会结合‘原始状态数据’自动计算出‘状态转移矩阵’,进而进行模型预测。
- 关于‘原始状态数据’:其指类似‘121313113’的状态数据。比如数字123分别代表移动、电信和联通,121313113指:移动->电信->移动->联通->移动->联通->移动->移动->联通。用户先使用移动然后再使用电信再使用移动再使用联通再使用移动再使用联通,来回这样的转移,系统会结合这样的转移计算出3种状态(3家运营商)的‘状态转移矩阵’。
操作
本例子操作如下:
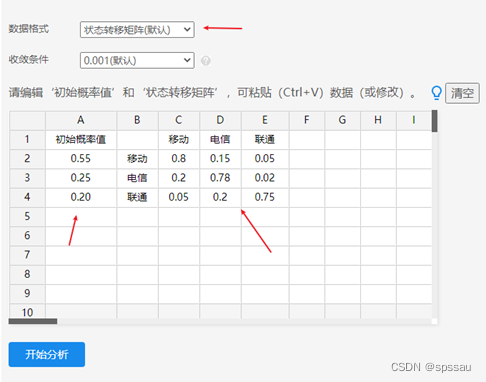
输入好初始概率值和状态转移矩阵,并且选择收敛条件为0.001(默认值),得到分析结果。另特别提示,有时候我们只有状态数据数字而没有转移概率,此时可自行计算出‘状态转移矩阵’后使用。也可直接选择状态数据序列,让SPSSAU自动计算‘状态转移矩阵’数据,操作如下图所示
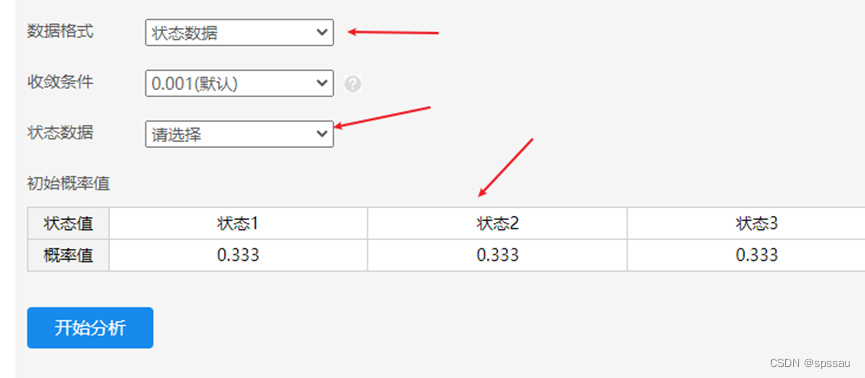
SPSSAU输出结果
SPSSAU共输出3个表格和1个图。分别如下说明:
| 表格或图 | 说明 |
| 基本信息 | 即初始概率值汇总表格 |
| 状态转移矩阵 | 展示状态转移矩阵数据 |
| 状态转移图 | 将状态转移矩阵使用图形形式展示出来 |
| 有限次状态转移概率分布图 | 展示马尔可夫预测的中间过程及结果 |
文字分析
| 基本信息 | |
| 项 | 初始概率 |
| 移动 | 0.55 |
| 电信 | 0.25 |
| 联通 | 0.2 |
上表格将初始概率值进行展示,无特别意义。
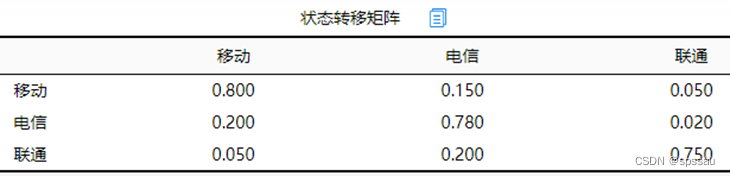
上表格中展示‘状态转移矩阵’表格,无特别意义。
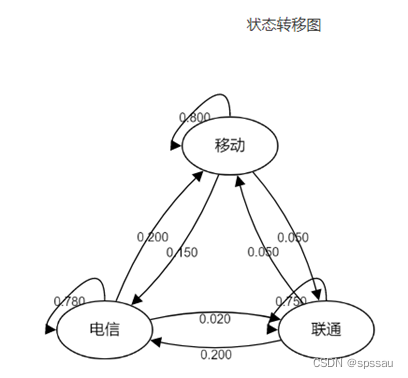
上图直观展示状态转移矩阵信息,比如移动用户明年还使用移动的可能性为0.8,明年使电信可能性为0.2,明年使用联通的可能性为0.05等。
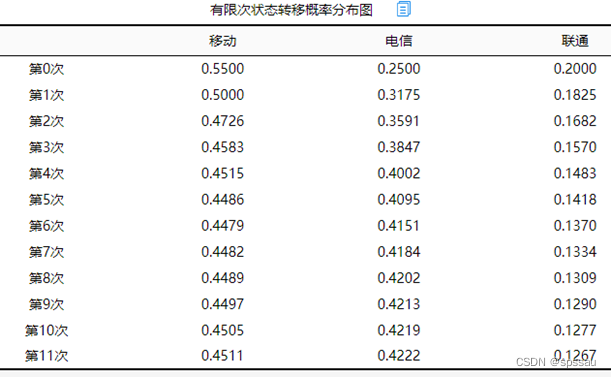
上表格展示‘有限次状态转移概率分布’,其实际意义为‘初始概率值’不停的变化不停的迭代过程,直至最终‘概率值’即市场份额稳定下来(误差低于‘收敛条件’即千分之1)。
第0次指初始概率值,即最初的市场份额占比情况。
经过10次的转移,即第10次时,模型已经收敛(即第9次和第10次的差值小于千分之1)。但SPSSAU依旧给出第11次的结果,用于进一步确认模型的收敛性。
即上述最终市场占比上,经过10次(或者10年后),移动、电信和联通3家运营商的市场占比分别是45.05%,42.19%和12.77%。最初时该占比依次为55%,25%和20%。显然移动和联通的用户有一部分均转移成电信用户。从数据角度可警示,只有企业持续创新服务用户,其才能保持市场优势永葆青春。
剖析
涉及以下几个关键点,分别如下:
- 马尔可夫预测的数据格式?
SPSSAU支持两种数据格式,分别是‘状态转移矩阵’和‘状态数据’。‘状态转移矩阵’要求提供‘初始概率值’和‘状态转移矩阵’。如果是‘状态数据’则需要提供‘初始概率值’和‘原始状态数据’,系统会结合‘原始状态数据’自动计算出‘状态转移矩阵’,进而进行模型预测。建议是提供‘状态转移矩阵’格式数据。