线索二叉树原理
遍历二叉树的其实就是以一定规则将二叉树中的结点排列成一个线性序列，得到二叉树中结点的先序序列、中序序列或后序序列。这些线性序列中的每一个元素都有且仅有一个前驱结点和后继结点。

但是当我们希望得到二叉树中某一个结点的前驱或者后继结点时，普通的二叉树是无法直接得到的，只能通过遍历一次二叉树得到。每当涉及到求解前驱或者后继就需要将二叉树遍历一次，非常不方便。

于是是否能够改变原有的结构，将结点的前驱和后继的信息存储进来。
————————————————
原文链接：https://blog.csdn.net/S_999999/article/details/86157532

总结：即利用起每个节点的空链域，使其指向其前驱或后继，排序后在头或为且有空领域没有前驱或后继则指向空。我们创建树的时候，定义lTag，lTag，都先赋值为0，当其左右子树为空时将l/rTag赋值为1.

树的图形状：

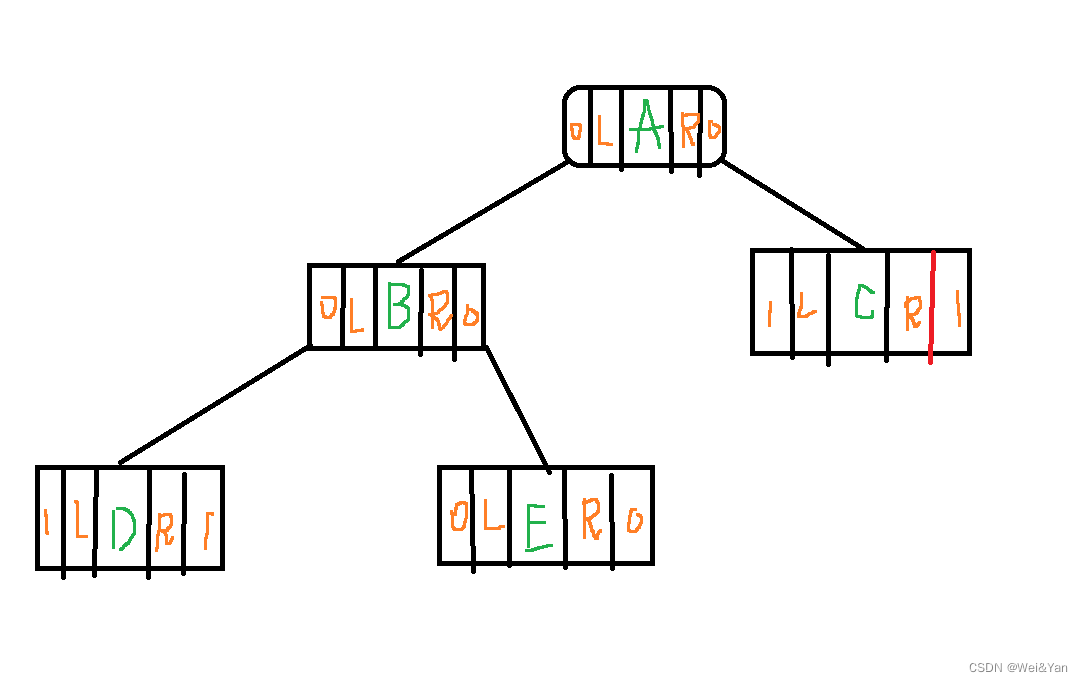
代码思路及其参代码（含讲解）

我们根据树的形状先创建其代码构建树

结构体的创建
typedef DataType;
typedef struct TreeNode
{
	DataType data;//存放的数据
	struct TreeNode* left, * right;//左右孩子指针
	int lTag, rTag;//左右是否为空领域的标志
}ThreadTreeNode;

 

构建树：
int main()
{
	ThreadTreeNode* A = (ThreadTreeNode*)malloc(sizeof(ThreadTreeNode));
	A->left = NULL;
	A->right = NULL;
	A->data = 'A';
	A->lTag = 0;
	A->rTag = 0;
	ThreadTreeNode* B = (ThreadTreeNode*)malloc(sizeof(ThreadTreeNode));
	B->left = NULL;
	B->right = NULL;
	B->data = 'B';
	B->lTag = 0;
	B->rTag = 0;
	ThreadTreeNode* C = (ThreadTreeNode*)malloc(sizeof(ThreadTreeNode));
	C->left = NULL;
	C->right = NULL;
	C->data = 'C';
	C->lTag = 0;
	C->rTag = 0;
	ThreadTreeNode* D = (ThreadTreeNode*)malloc(sizeof(ThreadTreeNode));
	D->left = NULL;
	D->right = NULL;
	D->data = 'D';
	D->lTag = 0;
	D->rTag = 0;
	ThreadTreeNode* E = (ThreadTreeNode*)malloc(sizeof(ThreadTreeNode));
	E->left = NULL;
	E->right = NULL;
	E->data = 'E';
	E->lTag = 0;
	E->rTag = 0;
	//赋值
	A->data = 'A';
	A->left = B;
	A->right = C;
	B->data = 'B';
	B->left = D;
	B->right = E;
    return 0；
}

 前序线索二叉树的构造

思路：

二叉树的线索化过程，分为两大步：

第一步：使用前序遍历，将二叉树线索化

1.定义一个全局变量当作前驱节点（每次节点遍历的时候其前驱节点一直在改变所以用全局变量）

preNode=NULL；

2. 使用前序遍历，递归的为每个节点线索化

a.给当前节点设置前驱节点

检查当前节点的左孩子节点是否为空

若为空，则对齐左指针线索化，指向preNode（上一次访问的节点）

若不为空，则递归的向左访问

b.给当前节点设置后继节点（给前一个节点设置其后继线索eg如我们上图的D判断其前一个节点B的右子树是否为空，若为空则右子树指向当前指针D，若不为空则不做处理）

c.设置当前节点为前一个节点（preNode的迭代）

3.前序访问的时候最后一个结点右指针没后继，则要单独处理让右指针的rTag赋值为1.

第二部：再定义一个函数，重新遍历线索二叉树

ThreadTreeNode* preNode = NULL;
void PreOrderThread(ThreadTreeNode* node)
{
	if (node == NULL)
	{//判空，若节点为空则直接返回
		return;
	}
	if (node->left == NULL)
	{//如果当前节点不为空且其左子树为空则对齐左子树进行线索化
		node->left = preNode;
		node->lTag = 1;
	}
//因为我们不知道后继节点，所以我们就遍历到下一个节点的时候再去设置上一个节点的的后继，此时上一个节点就是当前节点的前驱节点preNode，对其preNode的右子树进行判断
	if (preNode != NULL && preNode->right == NULL)
	{//如果前驱节点不为空且前驱节点的右孩子为空则对其设置后继（右子树线索化）
		preNode->right = node;
		preNode->rTag = 1;
	}
	preNode = node;//线索化完后我们让当前节点赋值为前驱节点使其进行迭代
	if (node->lTag == 0)//我们在访问其左子树的时候要先对其tag判断，如果其tag为0则说明其左子树不为空链域或还没有被线索化。如果我们不判断则当期访问ltag为1的节点则会访问到当前节点左子树线索化后指向的节点就是其前驱节点，这样会进入死循环，右子树同理也要进行判断
	{
		PreOrderThread(node->left);
	}
	if (node->rTag == 0)
	{
		PreOrderThread(node->right);
	}
}
//因为前序线索化时最后一个指针的右子树没有后继，则要对其单独处理，但也不能再函数递归过程中进行防止每次函数递归都会处理一次所以我们单独当整个递归完后再进行设置。
//解决方法：我们把线索化递归放进一个函数中，使其先进性线索化的递归，等整个线索化函数结束后再去处理最后一个指针，因为preNode一直在按前序顺序迭代，当迭代到最后一次的时候正好为最后一个节点，要让最后一个节点的rTag赋值为1，则直接让preNode的rTag为1即可。
void CreatePreOrderThread(ThreadTreeNode* root)
{
	preNode = NULL;
	if (root != NULL)
	{
		PreOrderThread(root);
		if (preNode != NULL)
		{
			preNode->rTag = 1;
		}
	}
}

 遍历线索化后的二叉树

 

利用递归思路进行遍历访问
void PreOrder(ThreadTreeNode* node)
{//先判空，不为空我们再进行处理
	if (node != NULL)
	{
		printf("%c->", node->data);
//我们再进行递归前先判断其lTag是否为0，如果为0则说明其左子树在线索化前不为空链域，则可以访问其左子树，如果不为0，则说明其左为空领域不能递归访问。我们不需要对右子树进行判断，因为右子树是否为空它都会按前序的顺序一直向后走不会出现循环
		if (node->lTag == 0)
		{
			PreOrder(node->left);
		}//lTag和rTag为串行关系，要么lTag要么rTag,我们不需要对右子树进行判断
		else
		{
			PreOrder(node->right);
		}
	}
}

总代码： 

#include <stdio.h>
#include  <stdlib.h>

typedef DataType;
typedef struct TreeNode
{
	DataType data;
	struct TreeNode* left, * right;
	int lTag, rTag;
}ThreadTreeNode;

ThreadTreeNode* preNode = NULL;
void PreOrderThread(ThreadTreeNode* node)
{
	if (node == NULL)
	{
		return;
	}
	if (node->left == NULL)
	{
		node->left = preNode;
		node->lTag = 1;
	}
	if (preNode != NULL && preNode->right == NULL)
	{
		preNode->right = node;
		preNode->rTag = 1;
	}
	preNode = node;
	if (node->lTag == 0)
	{
		PreOrderThread(node->left);
	}
	if (node->rTag == 0)
	{
		PreOrderThread(node->right);
	}
}
void CreatePreOrderThread(ThreadTreeNode* root)
{
	preNode = NULL;
	if (root != NULL)
	{
		PreOrderThread(root);
		if (preNode != NULL)
		{
			preNode->rTag = 1;
		}
	}
}
void PreOrder(ThreadTreeNode* node)
{
	if (node != NULL)
	{
		printf("%c->", node->data);
		if (node->lTag == 0)
		{
			PreOrder(node->left);
		}
		else
		{
			PreOrder(node->right);
		}
	}
}
int main()
{
	ThreadTreeNode* A = (ThreadTreeNode*)malloc(sizeof(ThreadTreeNode));
	A->left = NULL;
	A->right = NULL;
	A->data = 'A';
	A->lTag = 0;
	A->rTag = 0;
	ThreadTreeNode* B = (ThreadTreeNode*)malloc(sizeof(ThreadTreeNode));
	B->left = NULL;
	B->right = NULL;
	B->data = 'B';
	B->lTag = 0;
	B->rTag = 0;
	ThreadTreeNode* C = (ThreadTreeNode*)malloc(sizeof(ThreadTreeNode));
	C->left = NULL;
	C->right = NULL;
	C->data = 'C';
	C->lTag = 0;
	C->rTag = 0;
	ThreadTreeNode* D = (ThreadTreeNode*)malloc(sizeof(ThreadTreeNode));
	D->left = NULL;
	D->right = NULL;
	D->data = 'D';
	D->lTag = 0;
	D->rTag = 0;
	ThreadTreeNode* E = (ThreadTreeNode*)malloc(sizeof(ThreadTreeNode));
	E->left = NULL;
	E->right = NULL;
	E->data = 'E';
	E->lTag = 0;
	E->rTag = 0;
	//赋值
	A->data = 'A';
	A->left = B;
	A->right = C;
	B->data = 'B';
	B->left = D;
	B->right = E;
	CreatePreOrderThread(A);
	PreOrder(A);
		return 0;
}

运行结果：