0401概述-最短路径-加权有向图-数据结构和算法(Java)

news2024/10/6 12:24:13

文章目录

    • 1 最短路径
    • 2 最短路径的性质
    • 3 加权有向图的数据结构
      • 3.1 加权有向边
      • 3.2 加权有向图
    • 4 最短路径
      • 4.1 最短路径API
      • 4.2 最短路径的数据结构
      • 4.3 边的松弛
      • 4.4 顶点的松弛
    • 结语

1 最短路径

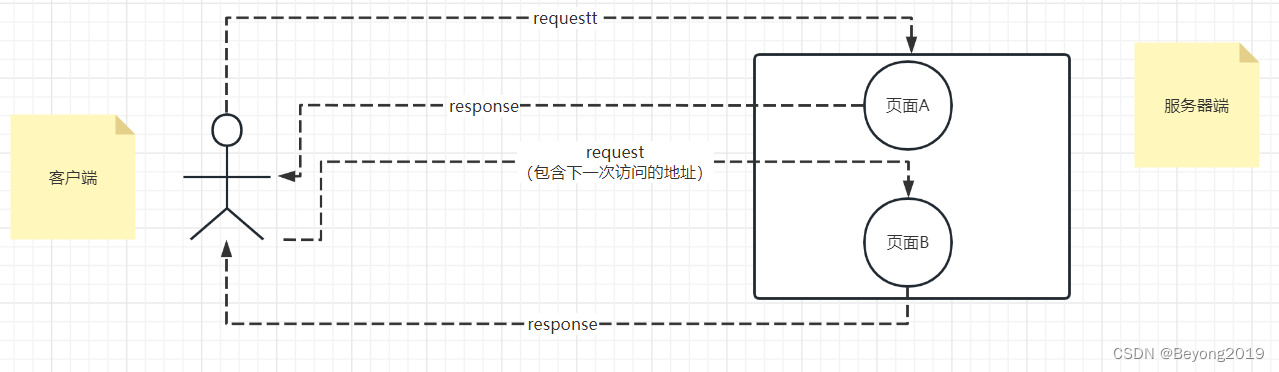
如图1-1所示，一幅加权有向图和其中的一条最短路径：

在这里插入图片描述

定义：在一幅加权有向图中，从顶点t到顶点s的最短路径是所有从s到t的路径中权重最小者。

**单点最短路径。**给定一幅加权有向图和一个起点s，回答“从s到给定目的顶点v是否存在一条有向路径？如果有，找出最短（总权重最小）的那条路径。“等类似问题。

2 最短路径的性质

最短路径问题的基本定义很简单，但是有些问题需要我们解决：

  • **路径上有向的。**最短路径需要考虑到各条边的方向。
  • **权重不一定等价于距离。**权重可以表示时间、花费等，也不一定 和距离的远近成正比。
  • **并不是所有顶点都是可达的。**如果t并不是从s可达的，那么就不存在任何路径，也就不存在从s到t到最短路径。为了简化问题，我们的样图都是强连通的。
  • **父权重会使问题更复杂。**我们暂时假设边的权重都是正的（或零），父权重在后面讨论。
  • 最短路径一般都是简单的。我们的算法会忽略构成环的零权重边，因此找到的最短路径都不会含有环。
  • **最短路径不一定是唯一的。**从一个顶点到达另一个顶点的权重最小的路径可能有多条，我们只要找到其中一条即可。
  • **可能存在平行边或自环。**平行边中的权重最小者才会被选中，最短路径也不可能包含自环（除非自环的权重为零，但我们会忽略它）。为零避免歧义我们隐式地假设平行边不存在，用v->w表示从v到w到边。

我们的重点是单点最短路径问题，其中给出起点s，计算的结果是一棵最短路径树（SPT），它包含了顶点s到所有可达到顶点的最短路径。如图2-1所示：

在这里插入图片描述

给定一幅加权有向图和一个顶点s，以s为起点的一颗最短路径树树图的一幅子图，它包含s和从s可达的所有顶点。这颗有向树的根结点为s，树中的每条路径都是有向图中的一条最短路径。

3 加权有向图的数据结构

3.1 加权有向边

有向边的数据结构比无向边简单，因为有向边只有一个方向，这里定义了from()和to()方法，API如下表3.1-1所示：

public classDirectedEdge
publicDirectedEdge(int v, int w, double weight)
public doubleweight()边的权重
public intfrom()指出这条边的顶点
public intto()这条边指向的顶点
public StringtoString()对象的字符串表示

有向边DirectedEdge源代码3.1-1如下所示：

package edu.princeton.cs.algs4;
/**
 *  有向边
 */

public class DirectedEdge { 
    /**
    * 边的起点
    */
    private final int v;
    /**
    * 边的终点
    */  
    private final int w;
    /**
    * 边的权重
    */  
    private final double weight;

    /**
     * 初始化权重weight，从顶点v指向w的有向边
     * @param v 边的起点
     * @param w 边的终点
     * @param weight 边的权重
     */
    public DirectedEdge(int v, int w, double weight) {
        if (v < 0) throw new IllegalArgumentException("Vertex names must be non-negative integers");
        if (w < 0) throw new IllegalArgumentException("Vertex names must be non-negative integers");
        if (Double.isNaN(weight)) throw new IllegalArgumentException("Weight is NaN");
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    /**
     * 返回边的起点
     * @return 边的起点
     */
    public int from() {
        return v;
    }

    /**
     * 边的终点
     * @return 边的终点
     */
    public int to() {
        return w;
    }

    /**
     * 边的权重
     * @return 边的权重 
     */
    public double weight() {
        return weight;
    }

    /**
     * 边的字符串表示
     * @return 边的字符串表示
     */
    public String toString() {
        return v + "->" + w + " " + String.format("%5.2f", weight);
    }
}

3.2 加权有向图

加权有向图API如下表3.2-1所示：

public classEdgeWeightedDigraph
publicEdgeWeightedDigraph(int V)初始化含有V个顶点的空有向图
publicEdgeWeightedDigraph(In in)从输入流读取取构造加权有向图
public intV()顶点总是
public intE()边的总数
public voidaddEdge(DirectedEdge e)添加一条有向边
public Iterable<DirectedEdge>adj(int v)从v指出的边
public Iterable<DirectedEdge>eges()该有向图的所有边
public StringtoString加权有向图的字符串表示

加权有向图EdgeWeightedDigraph 源代码3.2-1如下所示：

package edu.princeton.cs.algs4;

import java.util.NoSuchElementException;

/**
 *  加权有向图
 */
public class EdgeWeightedDigraph {
    private static final String NEWLINE = System.getProperty("line.separator");

    /**
    * 顶点总数
    */  
    private final int V;
  
    /**
    * 边的总数
    */  
    private int E;
  
    /**
    * 顶点指出的边
    */  
    private Bag<DirectedEdge>[] adj;
  
    /**
    * 入度
    */  
    private int[] indegree;
    
    /**
     * 初始化V个顶点的空有向图
     *
     * @param  V 顶点数
     */
    public EdgeWeightedDigraph(int V) {
        if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be non-negative");
        this.V = V;
        this.E = 0;
        this.indegree = new int[V];
        adj = (Bag<DirectedEdge>[]) new Bag[V];
        for (int v = 0; v < V; v++)
            adj[v] = new Bag<DirectedEdge>();
    }

    /**
     * 初始化v个顶点e条边的加权有向图
     *
     * @param  顶点总是
     * @param  边的总数
     */
    public EdgeWeightedDigraph(int V, int E) {
        this(V);
        if (E < 0) throw new IllegalArgumentException("Number of edges in a Digraph must be non-negative");
        for (int i = 0; i < E; i++) {
            int v = StdRandom.uniform(V);
            int w = StdRandom.uniform(V);
            double weight = 0.01 * StdRandom.uniform(100);
            DirectedEdge e = new DirectedEdge(v, w, weight);
            addEdge(e);
        }
    }

    /**  
     * 从输入流读取数据初始化加权有向图
     *
     * @param  输入流
     */
    public EdgeWeightedDigraph(In in) {
        if (in == null) throw new IllegalArgumentException("argument is null");
        try {
            this.V = in.readInt();
            if (V < 0) throw new IllegalArgumentException("number of vertices in a Digraph must be non-negative");
            indegree = new int[V];
            adj = (Bag<DirectedEdge>[]) new Bag[V];
            for (int v = 0; v < V; v++) {
                adj[v] = new Bag<DirectedEdge>();
            }

            int E = in.readInt();
            if (E < 0) throw new IllegalArgumentException("Number of edges must be non-negative");
            for (int i = 0; i < E; i++) {
                int v = in.readInt();
                int w = in.readInt();
                validateVertex(v);
                validateVertex(w);
                double weight = in.readDouble();
                addEdge(new DirectedEdge(v, w, weight));
            }
        }   
        catch (NoSuchElementException e) {
            throw new IllegalArgumentException("invalid input format in EdgeWeightedDigraph constructor", e);
        }
    }

    /**
     * 用一个加权有向图初始化加权有向图
     *
     * @param  加权有向图G
     */
    public EdgeWeightedDigraph(EdgeWeightedDigraph G) {
        this(G.V());
        this.E = G.E();
        for (int v = 0; v < G.V(); v++)
            this.indegree[v] = G.indegree(v);
        for (int v = 0; v < G.V(); v++) {
            // reverse so that adjacency list is in same order as original
            Stack<DirectedEdge> reverse = new Stack<DirectedEdge>();
            for (DirectedEdge e : G.adj[v]) {
                reverse.push(e);
            }
            for (DirectedEdge e : reverse) {
                adj[v].add(e);
            }
        }
    }

    /**
     * 顶点总数
     *
     * @return 顶点总是
     */
    public int V() {
        return V;
    }

    /**
     * 边的总数
     *
     * @return 边的总数
     */
    public int E() {
        return E;
    }

    /**
    * 校验顶点v
    */
    private void validateVertex(int v) {
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
    }

    /**
     * 添加一条有向边e
     *
     * @param  e 有向边e
     */
    public void addEdge(DirectedEdge e) {
        int v = e.from();
        int w = e.to();
        validateVertex(v);
        validateVertex(w);
        adj[v].add(e);
        indegree[w]++;
        E++;
    }


    /**
     * 顶点v的指出边
     *
     * @param  v 顶点v
     * @return 顶点v指出的边
     */
    public Iterable<DirectedEdge> adj(int v) {
        validateVertex(v);
        return adj[v];
    }

    /**
     * 顶点v的出度
     *
     * @param  v 顶点v
     * @return 顶点v的出度
     */
    public int outdegree(int v) {
        validateVertex(v);
        return adj[v].size();
    }

    /**
     * 顶点v的入度
     *
     * @param  v 顶点v
     * @return 顶点v的入度
     */
    public int indegree(int v) {
        validateVertex(v);
        return indegree[v];
    }

    /**
     * 所有边
     *
     * @return 所有边
     */
    public Iterable<DirectedEdge> edges() {
        Bag<DirectedEdge> list = new Bag<DirectedEdge>();
        for (int v = 0; v < V; v++) {
            for (DirectedEdge e : adj(v)) {
                list.add(e);
            }
        }
        return list;
    } 

    /**
     * 加权有向图的字符串表示
     * @return 加权有向图的字符串表示
     */
    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(V + " " + E + NEWLINE);
        for (int v = 0; v < V; v++) {
            s.append(v + ": ");
            for (DirectedEdge e : adj[v]) {
                s.append(e + "  ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }
}

加权有向图示意图3.2-1如下所示：

在这里插入图片描述

4 最短路径

4.1 最短路径API

public classSP
publicSP(EdgeWeightedDigraph G, int s)构造函数
public doubledistTo(int v)从顶点s到顶点v的距离，不存在路径为无穷大
public booleanhasPathTo(int v)是否存在从顶点s到v的路径
public Iterable<DirectedEdge>pathTo(int v)从顶点s到v的路径，不存在为null

4.2 最短路径的数据结构

表示最短路径 所需的数据结构很简单，如下图4.2-1所示：

在这里插入图片描述

  • 最短路径树中的边。使用一个由顶点索引的DirectedEdge对象的父链接数组edgeTo[],其中edgeTo[v]的值为连接v和它的父结点的边。
  • 到达起点的距离。由顶点索引的distTo[],其中distTo[v]表示从起点s到v的已知最短路径的长度。

我们约定edgeTo[s]为null，distTo[s]值为0。同时约定，从起点到不可达到顶点的距离均为Double.POSITIVE_INFINITY。

4.3 边的松弛

我们的最短路径API的实现都基于一个被称为松弛的操作。

  • 边的松弛。放松边v->w意味着检查从s到w到最短路径是否是先从s到v，然后在由v到w。如果是，则根据这个情况更新数据结构的内容。由v到w到最短路径是distTo[v]与e.weight()之和-如果这个值小于distTo[w],称这条边失效了并将它忽略；如果这个值更新，就更新数据。代码实现4.3-1如下所示：

        private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
        }
    }

如下图4.3-1所示：

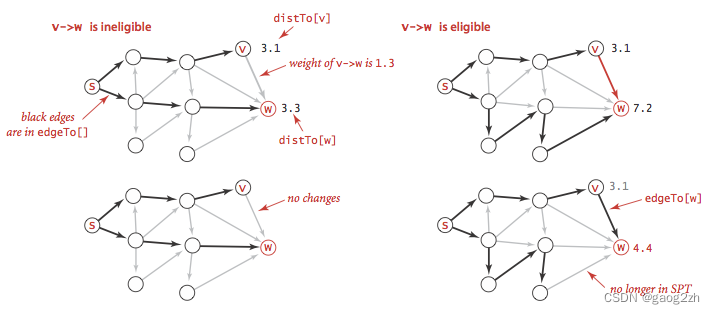
在这里插入图片描述

显示的是边的放松操作之后可能出现的两种情况。一种情况边失效（做边的例子），不更新任何数据；另外一种情况是v->w到达w的最短路径（右边的例子），这将会更新edgeTo[w]和distTo[w]。

4.4 顶点的松弛

实际上，实现会放松从一个顶点这出的所有边。从任意distTo[v]为有限值的顶点v指向任意distTo[]为无穷的顶点的边都是有效的。如果v被放松，那么这些有效边都会被添加到edgeTo[]中。某条从起点指出的边将会是第一天被加入edgeTo[]中的边。算法会谨慎选择起点，使得每次顶点松弛操作都能得出到达某个顶点的更短路径，最好逐渐找出到达某个顶点的最短路径。

顶点松弛代码4.4-1如下所示：

private void relax(EdgeWeightedDigraph G, int) {
	for(DirectedEdge e: G.adj(v)) {
		int w = e.to();
		if(distTo[w] > distTo[v]+ e.weight) {
			distTo[w] = distTo[v] + e.weight;
			edgeTo[w] = e;
		}
	}
}

结语

如果小伙伴什么问题或者指教，欢迎交流。

❓QQ:806797785

⭐️源代码仓库地址：https://gitee.com/gaogzhen/algorithm

参考链接:

[1][美]Robert Sedgewich,[美]Kevin Wayne著;谢路云译.算法：第4版[M].北京：人民邮电出版社，2012.10.p412-419.

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/461605.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

事务—MySQL

事务—MySQL

文章目录 1.事务的四大特性1.1原子性1.2一致性1.3隔离性1.4持久性 2.并发访问中存在的一些问题2.1丢失更新2.2脏读2.3不可重复读2.4幻读 3.隔离级别解决一致性的问题3.1未提交读3.2提交读3.3可重复读3.4可串行化 4.不同隔离级别可以解决的问题 1.事务的四大特性 1.1原子性 事…
阅读更多...
BBR原版/魔改/plus/锐速/七合一脚本linux加速脚本/硬盘挂载/cc防御/宝塔

BBR原版/魔改/plus/锐速/七合一脚本linux加速脚本/硬盘挂载/cc防御/宝塔

BBR原版/魔改/plus/锐速七合一脚本linux加速脚本/硬盘挂载/CC防御/宝塔 新云分享的七合一脚本&#xff0c;包含原版BBR、魔改BBR、bbrplus以及锐速可选。 在vultr上Centos 7, Debian 8/9, Ubuntu 16/18测试通过&#xff0c;不支持ovz。 安装指令&#xff1a;复制下面命令在s…
阅读更多...
Openswan安装和简单配置

Openswan安装和简单配置

Openswan安装和简单配置 安装环境&#xff1a; 操作系统&#xff1a;Ubuntu20.0.4TLS 用户权限&#xff1a;root下载Openswan: wget https://github.com/xelerance/Openswan/archive/refs/tags/v3.0.0.zip安装Openswan: 解压Openswan&#xff1a;&#xff08;PS&#xff1a…
阅读更多...
[golang gin框架] 26.Gin 商城项目-前台自定义商品列表模板, 商品详情数据渲染,Markdown语法使用

[golang gin框架] 26.Gin 商城项目-前台自定义商品列表模板, 商品详情数据渲染,Markdown语法使用

一.前台自定义商品列表模板 当在首页分类点击进入分类商品列表页面时&#xff0c;可以根据后台分类中的分类模板跳转到对应的模板商品列表页面 1.管理后台商品分类模板设置如下图所示 2.代码展示 (1).商品控制器方法Category()完善 修改controllers/frontend/productController…
阅读更多...
大模型竞逐，再造AI新格局

大模型竞逐，再造AI新格局

作者 | 辰纹 来源 | 洞见新研社 “面对AI时代&#xff0c;所有产品都值得用大模型重做一次。” 这是阿里巴巴集团董事会主席兼CEO、阿里云智能集团CEO张勇在2023阿里云峰会上对AIGC&#xff08;生成式AI&#xff09;进化的判断&#xff0c;在这背后则是由ChatGPT为起始点&…
阅读更多...
Shiro学习笔记，一篇就够用了

Shiro学习笔记，一篇就够用了

目录 一、Shiro基础 1.1Shiro定义: 1.2Shiro架构: 1.3快速上手: 二、Spring整合Shiro 2.1导入spring整合shiro的依赖 2.2两个配置类 寻找maven版本号:Maven Repository: org.apache.shiro shiro-core (mvnrepository.com) Shiro官网:Apache Shiro | Simple. Java. Securi…
阅读更多...
C. Trailing Loves (or L‘oeufs?)(求某个质因子在n的阶乘中的个数 + 思维)

C. Trailing Loves (or L‘oeufs?)(求某个质因子在n的阶乘中的个数 + 思维)

Problem - C - Codeforces Aki喜欢数字&#xff0c;尤其是那些带有尾随零的数字。例如&#xff0c;数字9200有两个尾随零。Aki认为数字拥有的尾随零越多&#xff0c;它就越漂亮。 然而&#xff0c;Aki认为&#xff0c;一个数字拥有的尾随零的数量并不是固定的&#xff0c;而是…
阅读更多...
微搭低代码调用第三方API

微搭低代码调用第三方API

目录 1 创建项目2 获取实时天气API3 创建APIs4 小程序中调用总结 应粉丝要求&#xff0c;我们本篇介绍一下微搭中如何调用第三方API。我们的应用开发中比较常见的一类需求是开发一个天气的功能&#xff0c;方便用户访问应用的时候实时的看到今天最新的天气情况。 第三方的天气…
阅读更多...
虚拟机安装使用经验

虚拟机安装使用经验

1 VMware 跟 VirtualBox 在网络上可以看到很多对比的资料&#xff0c;比如这篇: VirtualBox 和 VMware的区别 VMware 分商业版跟非商业版&#xff0c;我们这里仅讨论非商业版&#xff0c;也就是 VMware Workstation Player&#xff0c;支持在 Linux、Windows、Mac OS 等系统上…
阅读更多...
docker容器：Docker consul的容器服务更新与发现

docker容器：Docker consul的容器服务更新与发现

目录 一、Docker consul 1、什么是服务注册与发现 2、什么是consul 3、consul部署 ①实验目的 ②实验环境及拓扑 ③consul配置 ④registrator后端配置 ⑤测试发现功能是否正常 4、consul-template部署 ①准备template nginx模板文件 ②编译安装nginx ③安装templa…
阅读更多...
LVS-keepalived

LVS-keepalived

文章目录 一、keepalived1、KEEPALIVED作用2、KEEPALIVED原理3、KEEPALIVED工作模式4、KEEPLIVED问题及优化 二、实验1.LVSKeepalived 高可用群集 总结 一、keepalived 1、KEEPALIVED作用 保证负载均衡的高可用性&#xff0c;完美解决了LVS所有问题&#xff0c;可以检查后端服…
阅读更多...
【随笔】转发/转向(服务器重定向，服务器转发，服务器跳转)和重定向（客户端重定向，客户端转发，客户端跳转）

【随笔】转发/转向(服务器重定向，服务器转发，服务器跳转)和重定向（客户端重定向，客户端转发，客户端跳转）

文章目录 1.转发&#xff08;转向&#xff09;和重定向图解2.例子3.区别 1.转发&#xff08;转向&#xff09;和重定向图解 图&#xff1a;转发&#xff08;转向&#xff09; 图&#xff1a;重定向 2.例子 转发&#xff1a;A找B要钱&#xff0c;B没钱&#xff0c;于是B向C…
阅读更多...
OSPF路由协议解释

OSPF路由协议解释

目录 OSPF路由协议OSPF数据包类型OSPF邻区状态OSPF的邻接关系建立过程 路由名词解释OSPF开源项目 OSPF路由协议 OSPF简介 1、&#xff08;Open Shortest Path First&#xff09;&#xff0c;开放式最短路径优先&#xff0c;它属于链路状态路由协议&#xff0c;大部分路由将由O…
阅读更多...
ChatGPT进化的过程简介

ChatGPT进化的过程简介

Chat GPT可以做什么&#xff1f; 分点列条的回答问题 写代码或SQL 翻译 语法检查 ChatGPT官方还未公开论文&#xff0c;ChatGPT有一个“孪生兄弟”InstructGPT&#xff0c;InstructGPT有论文&#xff0c;可以根据InstructGPT论文推导ChatGPT的训练过程&#xff1a; ChatGPT的…
阅读更多...
React函数组件语法(N)

React函数组件语法(N)

文章目录 react学习的说明新的官网全力投入现代React与Hooks React简介概述官网特点生态 React脚手架create-react-app官网创建和启动项目项目结构sass支持 Vite创建和启动项目项目结构常见配置 虚拟DOM什么是虚拟DOM虚拟DOM优缺点优点&#xff1a;缺点&#xff1a; 虚拟DOM实现…
阅读更多...
MySQL死锁的原因和处理方法

MySQL死锁的原因和处理方法

MySQL死锁的原因和处理方法 表的死锁产生原因解决方案 行级锁死锁产生原因1解决方案1产生原因2产生原因3解决方案 表的死锁 产生原因 用户A访问表A(锁住了表A),然后又访问表B&#xff1b;另一个用户B访问表B(锁住了表B),然后企图访问表A;这时用户A由于用户B已经锁住表B,它必须…
阅读更多...
LeetCode349. 两个数组的交集

LeetCode349. 两个数组的交集

题目链接 LeetCode349. 两个数组的交集 题目描述 题解 题解一&#xff08;Java&#xff09; 作者&#xff1a;仲景 因为数据范围和长度都限制在1000&#xff0c;所以直接使用数组即可 因为数据范围和长度都在1000内&#xff0c;所以碰到数字可以直接arr[i] i来表示这个数字…
阅读更多...
如何有效的开展接口自动化测试，一篇就行

如何有效的开展接口自动化测试，一篇就行

一、简介 接口自动化测试是指使用自动化测试工具和脚本对软件系统中的接口进行测试的过程。其目的是在软件开发过程中&#xff0c;通过对接口的自动化测试来提高测试效率和测试质量&#xff0c;减少人工测试的工作量和测试成本&#xff0c;并且能够快速发现和修复接口错误&…
阅读更多...
手写Spring框架---IOC容器实现

手写Spring框架---IOC容器实现

目录 框架具备的最基本功能 实现容器前奏 创建注解 提取标记对象 extractPacakgeClass里面需要完成的事情 获取项目类加载器的目的 为什么不让用户传入绝对路径 类加载器ClassLoader 统一资源定位符URL ClassUtil提取标记类 获取包下类集合 装载目标类的集合 获取…
阅读更多...
Git相关使用

Git相关使用

私人博客 许小墨のBlog —— 菜鸡博客直通车 系列文章完整版&#xff0c;配图更多&#xff0c;CSDN博文图片需要手动上传&#xff0c;因此文章配图较少&#xff0c;看不懂的可以去菜鸡博客参考一下配图&#xff01; 系列文章目录 前端系列文章——传送门 后端系列文章——传送…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023