目录
前言
一、概述
1.相关定义
(1)层
(2)分层抽样
2.分层随机抽样的步骤
3.分层抽样优于简单随机抽样的理由
4.分层原则
5.例
(1)
(2)
6.符号
二、简单估计量及其性质
1.总体均值的估计
2.总体均值估计的性质
(1)【定理3.1】
(2)【定理3.2】
(3)【定理3.3】
(4)【定理3.4】
(5)【推论3.1】
3.【例3.1】
三、比率估计量及其性质
四、回归估计量及其性质
五、各层样本量的分配
六、总样本量的确定
七、分层抽样的其他方面
前言
为什么采用分层抽样?
- 当总体规模N和样本量n都较大时,总体单位之间差异也较大,容易使随机抽出的不具有代表性。此时进行简单随机抽样成本高,精度低
- 如调查北京市大一学生的平均身高,由于男生一般比女生高,用简单随机抽样可能大多抽到男生或女生,出现过于偏向某一部分的不平衡情况,使样本不具有代表性,使估计结果偏高或偏低。应以性别为分层变量,采用分层抽样的方法
解决方法?
- 在保证估计精度的前提下,设法缩小总体规模N与需要抽取的样本数n,通过将总体划分为若干层达到该目的
- 尽量使样本总体与目标总体结构相似,方法是将总体依照与调查研究关注的变量高度相关的指标划分成几个层,使满足层内差异小、层间差异大的分层原则。例如研究居民收入,可用年龄、性别、学历等作为分层变量
一、概述

1.相关定义
(1)层
如果一个包含N个单位总体可以分成互不交叉(“不重不漏”)的L个子总体,即每个单元必属于且仅属于一个子总体,则称这样的子总体为层(stratum)。
设L个子总体包含的单位数分别为,则有
。
(2)分层抽样
在每一层中独立进行简单随机抽样,所得到的样本称为分层样本。总的样本由各层样本组成,总体参数则根据各层样本参数汇总做出估计,这种抽样就成为分层抽样(stratified sampling)。
如果每层都是独立地按照简单随机抽样进行,那么这样的分层抽样称为分层随机抽样。
设总的样本量为n,从L个子总体中所抽取的样本量分别为,则有
。
2.分层随机抽样的步骤
- 将抽样总体划分为层
- 在各层内独立地进行简单随机抽样,估计出层的参数
- 将各层参数的估计值按各层样本量在总体中所占比例(层权)进行加权,汇总得到总体参数的估计
3.分层抽样优于简单随机抽样的理由
- 每层都抽样,样本更具有代表性;样本结构与总体结构更相似(例如调查我国人口出生性别比,如采用简单随机抽样,一些人口少的地区可能没有单元入样,分层抽样保证各地区都有样本入样)
- 抽样在各层独立进行,一则可以在各层选择合适本层的不同抽样方法,二则可以同时对各层进行参数估计(例如全国性居民收入状况调查,以各省居民为子总体进行分层抽样,不仅可以得到全国居民收入水平,而且可以同时得到各省居民收入水平)
- 分层抽样的抽样效率较高。也就是说分层抽样的估计精度较高,是因为分层抽样估计量的方差只和层内方差成正比,和层间方差无关
- 各层抽样方法可以不同,而且便于因地制宜组织抽样工作
4.分层原则
分层随机抽样中,划分层的指标应与关心的调查变量有较强相关性。
- 估计:层内单元具有相同性质,通过按调查对象的不同类型进行划分
- 精度:尽可能使层内单元的指标值相近,层间单元的差异尽可能大,从而达到提高抽样估计精度的目的
- 估计和精度:既按类型,又按层内单元指标值相近的原则进行分层,同时达到估计类值以及提高估计精度的目的
- 实施:为抽样组织实施的方便,常按行政管理机构设置进行分层
5.例
(1)
对全国范围汽车运输的抽样调查,调查目的不仅要推算全国货运汽车完成的运量,还要推算不同经济成分(国有、集体、个体)汽车完成的运量
- 为组织方便,首先将货运汽车总体按省分层,由各省运输管理部门负责省内的调查工作
- 各省再将省内拥有的汽车按经济成分分层
(2)
某高校对学生在宿舍使用电脑的情况进行调查,根据经验,本科生和研究生使用电脑的状况差异较大
- 在抽样前对学生按本科生和研究生进行分层是有必要的
6.符号
| 层号 | |
| 第h层单元总数 | |
| 第h层样本单元数 | |
| 第h层第i个样本单元取值 | |
| 第h层的层权 | |
| 第h层的抽样比 | |
| 第h层的总体均值 | |
| 第h层的样本均值 | |
| 第h层的总体方差 | |
| 第h层的样本方差 |
二、简单估计量及其性质
1.总体均值的估计
【注】分层抽样中,所有总体参数的估计量都采用下标“st”以示区别
分层简单随机样本,总体均值的简单估计为
2.总体均值估计的性质
(1)【定理3.1】
对于分层随机抽样,是
的无偏估计。
(2)【定理3.2】
对于分层抽样,有。
- 只要对各层估计量无偏,则总体估计量也无偏
- 由于各层独立抽取,上式中红色部分为0
(3)【定理3.3】
对于分层随机抽样,的估计量
具有如下性质
(4)【定理3.4】
对于分层随机抽样,的方差
的无偏估计量为
其中,是第h层的样本方差。
各层内独立进行简单随机抽样,由定理2.4。
(5)【推论3.1】
对于分层随机抽样,为
的无偏估计。总体总量
的估计量
有如下性质:
,
是
的一个无偏估计
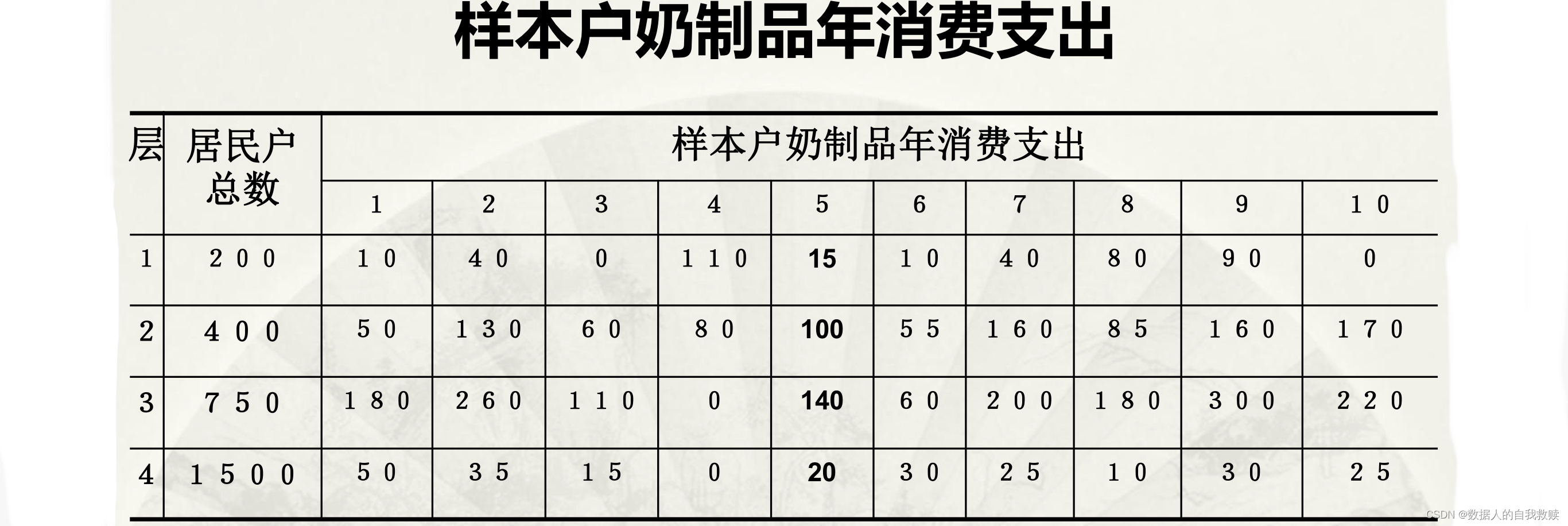
3.【例3.1】




![[附源码]Python计算机毕业设计Django大学生创新项目管理系统](https://img-blog.csdnimg.cn/7e4d74cc0c1a44c88eaf46e1f9c1dbd7.png)






![[附源码]SSM计算机毕业设计学生量化考核管理系统JAVA](https://img-blog.csdnimg.cn/63ce37d0bd244a22a25a090a475fece8.png)
![[附源码]Python计算机毕业设计Django常见Web漏洞对应POC应用系统](https://img-blog.csdnimg.cn/3e56d44262cb4c6d9150eaaca452156a.png)