1.算法描述

人们通过群体行为的研究可以揭示群体智能的产生，群体智能是自组织的过程，将简单的个体通过交互作用或协作表现出来整体智能行为的特性称为“群体智能”。

“群体智能”应用到的算法有哪些？

群体智能可以应用到优化算法中，如遗传优化算法、蚁群优化算法、粒子群优化算法等。另一方面，受群体智能行为的启发，人们可以借鉴生物的智慧，将群体智能应用到多机器人系统协同控制的研究，通过设计一定的控制算法或应用群体智能优化算法，可以使系统整体呈现出所期望的行为。

群体无人机和群体智能的联系：

群体无人机的英文名称为Swarm UAVs，是指由一组无人机构成的群体。目前对于群体无人机的定义目前还没有一个明确的定论，但从有关群体机器人的文献来看,比较一致的观点是:群体无人机是由一组具有自主能力的同构无人机构成的群体系统，群中无人机是具备局部通信和感知能力的相对简单自治个体，群体中没有集中的控制单元，但众多无人机的群体行为却能体现群体智能的特性。

群体无人机作为一种受群体智能启发的特殊多无人机系统，除了具有一般多无人机系统的特点外，还具有自身的优点:

1)群体系统结构是基于局部感知或通信的分布式体系结构，采用分布式控制策略，因此，系统具有很强的可扩展性;

2)群体中的个体相对简单，使得无人机的物理实现更加容易，生产成本低;

3)采用分布式控制策略，群体具有自组织的协调控制能力，群体系统对局部个体失效和故障不敏感，系统具有强鲁棒性。

正因为上述的可扩展性、鲁棒性强、适应性强和个体简单的优点，使得群体无人机具有良好的应用前景，特别是以下几种类型的任务很适合于群体无人机:

1)区域监测/遍历类任务。群体无人机是分布式系统，很适合于用来协同感知和监测空间状态。例如，在某一区域受灾时，通过构建一群微型自主无人飞行器组成的群体系统，可以对地面受灾状况协同监测，同时可以为地面用户提供应急的通信网络;

2)外界环境过于危险的任务。由于群体系统中个体无人机的造价成本低，而且个体的故障或坠毁不影响群体的整体行动规划，所以群体无人机适合用来执行蕴藏危险的任务，以牺牲部分个体成员的方式换整体的胜利，如无人战斗机的集群作战等。

3)有冗余性要求的任务。群体无人机系统具有强鲁棒性，这里的鲁棒性是指在群体中部分个体的失效和故障情况下，系统能正常运作。该鲁棒性决定了群体无人机适合执行有冗余性要求的任务。例如，在战场环境中，群体无人机能临时构建动态的通信网络。

4)群体规模可及时伸缩的任务。例如，在敌方火力越来越凶猛的情况下，可扩大群体规模集中火力攻击敌方阵地。

无人机集群以其高度的灵活性、广泛的适应性、可控的经济性,拥有越来越广泛的应用潜力,受到国内外的高度关注。任务规划是无人机集群应用的顶层规划，是根据任务环境态势、任务需求、自身特性等要求进行的综合调度，从而建立无人机与任务的合理映射关系，维持机间合理协同合作关系。本文从基于逻辑与规则的自上而下式任务规划和基于集群智能涌现的自下而上式任务规划两个方面,对无人机集群任务规划技术现状进行了全面的总结,分析了当前无人机集群任务规划技术研究应当关注的若干发展方向。针对多智能体蜂拥控制过程中个体间的差异性,在包含多个虚拟领导者的情况下,研究了针对多智能体个体差异性的优化蜂拥控制算法.首先,在Olfati-Saber算法避碰,聚合和速度匹配的基础上引入多智能体之间的质量差异策略,实现多智能体的聚合和速度匹配;其次,在多领导者的影响下,对引领反馈进行优化,研究了智能体个体跟踪多领导者的控制算法.最后,通过实验仿真,验证了基于改进Olfati-Saber算法的多智能体蜂拥控制算法可以实现多智能体蜂拥运动状态。

虚拟领导者可以看作是提前给定的预定路线，蜂拥控制的目的是多智能体不仅要达到蜂拥状态而且还要按照预定路线移动，如来自地面指挥员的命令。本文考虑了切换拓扑结构，因此把每个智能体的邻域可以看作是时间t的函数。两个智能体之间的距离超过感应半径时，它们之间的连边会断开，有可能整个多智能体网络会不连通。本文采用动态牵制策略达到多智能体网络蜂拥控制目标。

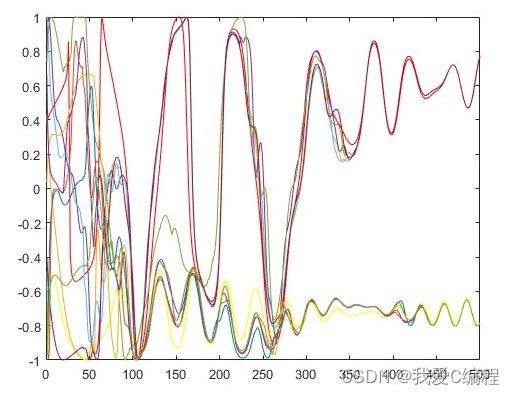
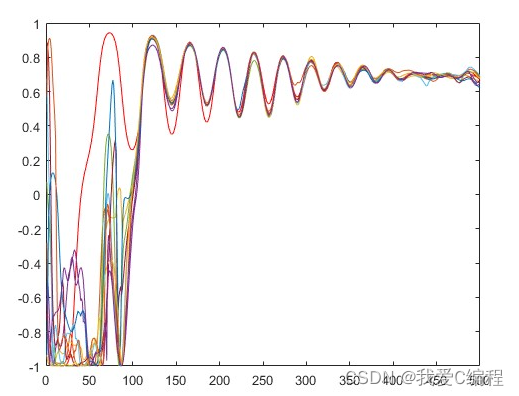
2.仿真效果预览

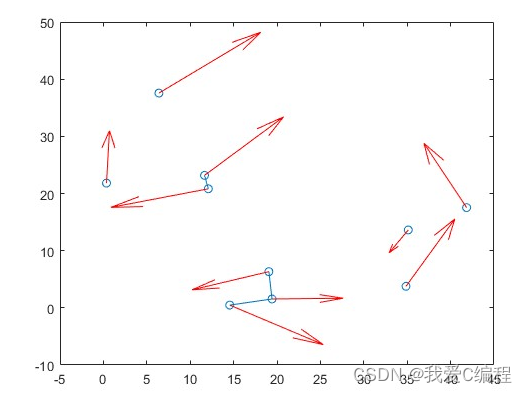
matlab2022a仿真结果如下：

3.MATLAB核心程序

    %-----------------求智能体的位置影响------------------
    %求u11=fya*N（i,j）
    u11=zeros(n,n,2);
    for i=1:n
        for j=1:n
            u11(i,j,1)=fya(i,j)*N(i,j,1);
            u11(i,j,2)=fya(i,j)*N(i,j,2);
        end
    end
    u1=zeros(2,n);
    for i=1:n
        for j=1:n
            u1(1,i)=u1(1,i)+u11(i,j,1);
            u1(2,i)=u1(2,i)+u11(i,j,2);
        end
    end
    %----------------求智能体的速度影响----------------------
    %求u22=aij*(pj-pi-prj+pri)
    u22=[n,n,2];
    for i=1:n
        for j=1:n
            u22(i,j,1)=A(i,j)*(p(1,j)-p(1,i)-pr(1,i)+pr(1,i));
            u22(i,j,2)=A(i,j)*(p(2,j)-p(2,i)-pr(2,i)+pr(2,i));
        end
    end
    %u2为反馈2
    u2=zeros(2,n);
    for i=1:n
        for j=1:n
            u2(1,i)= u22(i,j,1)+ u2(1,i);
            u2(2,i)= u22(i,j,2)+ u2(2,i);
        end
    end
    %-----------------求领导者的影响------------------
    u3=zeros(2,n);
    for i=1:5
        u3(1,i)=-c1*(q(1,i)-qr1(1,1))-c2*(p(1,i)-pr1(1,1));
        u3(2,i)=-c1*(q(2,i)-qr1(2,1))-c2*(p(2,i)-pr1(2,1));
    end
    for i=6:10
        u3(1,i)=-c1*(q(1,i)-qr2(1,1))-c2*(p(1,i)-pr2(1,1));
        u3(2,i)=-c1*(q(2,i)-qr2(2,1))-c2*(p(2,i)-pr2(2,1));
    end
    %-----------------求加速度u---------------------------
    %----各智能体在计算时加入其领导智能体的加速度反馈ur------
    u=zeros(2,n);
    for i=1:2
        for j=1:5
          u(i,j)=u1(i,j)+u2(i,j)+u3(i,j)+ur1(i,1);
        end
    end
    for i=1:2
        for j=6:10
          u(i,j)=u1(i,j)+u2(i,j)+u3(i,j)+ur2(i,1);
        end
    end
    %----------------进行下一步运算--------------
    %-------------智能体离散计算------------
    for i=1:2
        for j=1:n
            q(i,j)=q(i,j)+step*p(i,j);
            p(i,j)=p(i,j)+step*u(i,j);
        end
    end
    %------------虚拟领导者离散计算------------
    for i=1:2
        qr1(i,1)=qr1(i,1)+step*pr1(i,1);
        pr1(i,1)=pr1(i,1)+step*ur1(i,1);
    end
    for i=1:2
        qr2(i,1)=qr2(i,1)+step*pr2(i,1);
        pr2(i,1)=pr2(i,1)+step*ur2(i,1);
    end
 
end
%---------------------循环结束，绘图------------------------
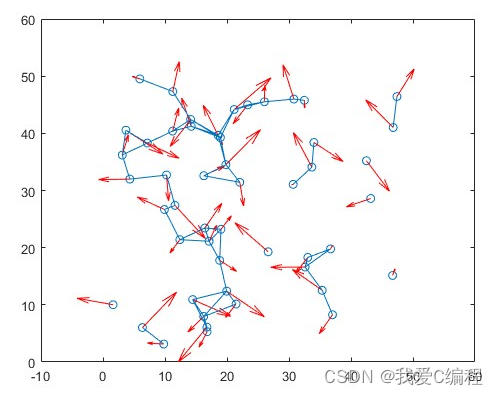
%---------------------智能体初始时刻状态--------------------
figure(1);
plot(qq(1,:,1),qq(2,:,1),'o');
hold on;
quiver(qq(1,:,1),qq(2,:,1),pp(1,:,1),pp(2,:,1),'Color','red');
for i=1:n
    for j=1:n
        if sqrt((qq(1,i,1)-qq(1,j,1))^2+(qq(2,i,1)-qq(2,j,1))^2)<=r
            line([qq(1,i,1),qq(1,j,1)],[qq(2,i,1),qq(2,j,1)]); 
        end
    end
end
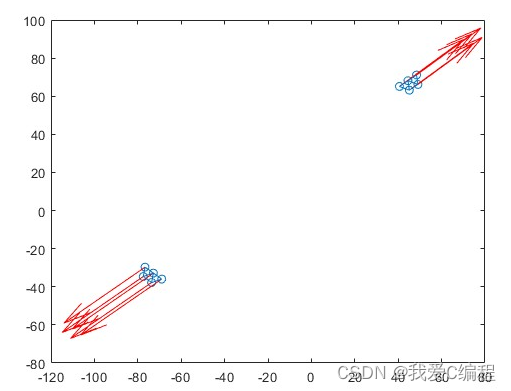
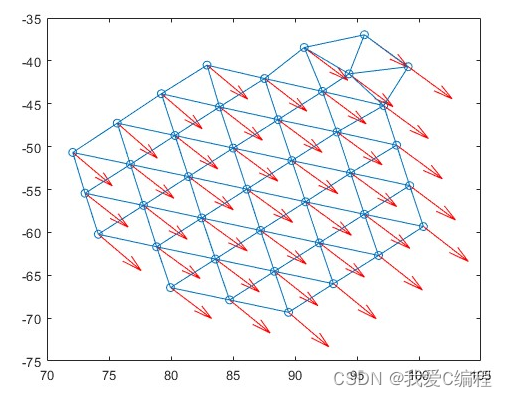
%-------------------智能体最终时刻状态---------------
figure(2);
plot(qq(1,:,loop),qq(2,:,loop),'o');
hold on;
quiver(qq(1,:,loop),qq(2,:,loop),pp(1,:,loop),pp(2,:,loop),'Color','red');
for i=1:n
    for j=1:n
        if sqrt((qq(1,i,loop)-qq(1,j,loop))^2+(qq(2,i,loop)-qq(2,j,loop))^2)<=r
            line([qq(1,i,loop),qq(1,j,loop)],[qq(2,i,loop),qq(2,j,loop)]); 
        end
    end
end
%--------------------智能体t时刻--------------------------------
a77