数据结构与算法（五）：算法专项 Hash、BitMap、Set、布隆过滤器、中文分词、Lucene 倒排索引

news2025/1/11 18:08:51

算法专项 Hash、BitMap、Set、布隆过滤器、中文分词、Lucene 倒排索引

Hash

思考：

  1. 给你N（1<N<10）个自然数,每个数的范围为（1~100）。现在让你以最快的速度判断某一个数是否在这N个数内，不得使用已经封装好的类，该如何实现
  2. 给你N（1<N<10）个自然数,每个数的范围为（1~10000000000）。现在让你以最快的速度判断某一个数是否在这N个数内，不得使用已经封装好的类，该如何实现。 A[] = new int[N+1]？

散列表

散列表英文就是Hash Table，也就是我们经常说的哈希表，大家肯定经常听到，其实刚刚上面我们的那个例子就是运用了散列表的思想来解决的

散列表用的是数组支持按照下标随机访问数据的特性，散列表其实就是数组的一种扩展，由数组演化而来。可以说，如果没有数组，就没有散列表

实际上，这个例子已经用到了散列的思想。在这个例子里，N自然数，并且与数组的下标形成一一映射，所以利用数组支持根据下标随机访问的特性

查找的时间复杂度是O(1)这一特性，就可以实现快速判断元素是否存在序列当中

Hash冲突

开放寻址：开放寻址法的核心思想是，如果出现了散列冲突，我们就重新探测一个空闲位置，将其插入

当我们往散列表中插入数据时，如果某个数据经过散列函数散列之后，存储位置已经被占用了，我们就从当前位置开始，依次往后查找，看是否有空闲位置，直到找到为止。

缺点：

  1. 删除需要特殊处理
  2. 插入的数据如果过多会导致散列表很多冲突查找可能会退化成遍历

链路地址：使用链表, 链表法是一种更加常用的散列冲突解决办法，相比开放寻址法，它要简单很多

HashMap Hash冲突之链表优化

由于链表这种结构确实存在一些缺点，所以在我们的JDK中对之进行了优化，引入了更高效的数据结构：

红黑树

  1. 初始大小：HashMap默认的初始大小是16，这个默认值是可以设置的，如果事先知道大概的数据量有多大，可以通过修改默认初始大小，减少动态扩容的次数，这样会大大提高HashMap的性能

  2. 动态扩容：最大装载因子默认是0.75，当HashMap中元素个数超过0.75*capacity（capacity表示散列表的容量）的时候，就会启动扩容，每次扩容都会扩容为原来的两倍大小

  3. Hash冲突解决办法：JDK1.7底层采用链表法。在JDK1.8版本中，为了对HashMap做进一步优化，我们引入了红黑树。而当链表长度太长（默认超过8）时，链表就转换为红黑树。我们可以利用红黑树快速增删改查的特点，提高HashMap的性能。当红黑树结点个数少于8个的时候，又会将红黑树转化为链表。因为在数据量较小的情况下，红黑树要维护平衡，比起链表来，性能上的优势并不明显

int hash(Object key) {
 int h = key.hashCode()；
 return (h ^ (h >>> 16)) & (capitity -1); //capicity表示散列表的大小,最好使用2的整数倍
}

设计高效的企业级Hash表

这里大家可以借鉴HashMap 的设计思路：

  1. 必须要高效：即插入，删除 查找必须要快
  2. 内存：不能占用太多的内存,考虑用其他的结构，比如B+Tree，HashMap 10亿，存硬盘的算法：mysql B+tree
  3. Hash函数：这个要根据实际情况考虑.%
  4. 扩容:就是预估数据的大小，HashMap 默认的空间是16？ 我知道我要存10000个数，2^n > 10000 or 2^n-1
  5. Hash冲突后怎么解决：链表 数组

Hash应用

  1. 加密：MD5 哈希算法，不可逆
  2. 判断视频是否重复
  3. 相似性检测
  4. 负载均衡
  5. 分布式分库分表
  6. 分布式存储
  7. 查找算法 HashMap

Hash扩容算法在多线程时问题

  1. 多线程put操作，get会死循环()。这个确实可以优化掉，比如扩容的时候我们新开一个数组，不要使用共享的那个数组
  2. 多线程put可能会导致get取值错误

为什么会出现死循环呢？

  1. hash冲突时我们会采用了链式结构来保存冲突的值。如果我们在遍历这个链表时本身是这样的1->2->3->null
  2. 如果我们遍历到3本身应该是null的，这时候刚好有人把这个null给计算出了值，null => 1->3，这下就完了 原来的3本来是要指向null结束的 这下又变成指向1，而这个1又刚好指向3 ，这样是不是就一直循环下去了

BitMap

场景

  • 数据判重
  • 不重复数据排序

缺点

  • 数据不能重复
  • 数据量少时没有优势
  • 无法处理字符串hash冲突

思考：如何在3亿个整数（0~2亿）中判断某一个数是否存在？内存限制500M，一台机器

  • 分治：
  • 布隆过滤器：神器
  • Redis
  • Hash: 开3亿个空间，HashMap（2亿） ？
  • 数组：年龄问题；data[2亿] ？
  • Bit：bitMap，位图；

类型基础：计算中最小的内存单位是bit，只可以表示0，1

  • 1Byte = 8bit
  • 1int = 4byte 32bit
  • Float = 4byte 32bit
  • Long=8byte 64bit
  • Char 2byte 16bit

Int a = 1,这个1在计算中是怎么存储的？
0000 0000 0000 0000 0000 0000 0000 0001 toBinaryString (1) =1

运算符基础

左移 <<

  • 8 << 2 = 8 * (2 ** 2) = 8 * 4 = 32
  • 8 << 1 = 8 * (2 ** 1) = 8 * 2 = 16
    0000 0000 0000 0000 0000 0000 0000 1000
    << 2
    0000 0000 0000 0000 0000 0000 0010 0000

右移 >>

  • 8 >> 2 = 8 / (2 ** 2) = 8 / 4 = 2
  • 8 >> 1 = 8 / (2 ** 1) = 8 / 2 = 4
    0000 0000 0000 0000 0000 0000 0000 1000
    >> 2
    0000 0000 0000 0000 0000 0000 0000 0010

位与 &

  • 8 & 7
    0000 0000 0000 0000 0000 0000 0000 1000 = 8
    &
    0000 0000 0000 0000 0000 0000 0000 0111 = 7
    =
    0000 0000 0000 0000 0000 0000 0000 0000 = 0

位或 |

  • 8 | 7
    0000 0000 0000 0000 0000 0000 0000 1000 = 8
    &
    0000 0000 0000 0000 0000 0000 0000 0111 = 7
    =
    0000 0000 0000 0000 0000 0000 0000 1111 = 23 + 22 + 21 + 20 = 8+4+2+1=15

BitMap

一个int占32个bit位。假如我们用这个32个bit位的每一位的值来表示一个数的话是不是就可以表示32个数字，也就是说32个数字只需要一个int所占的空间大小就可以了，瞬间就可以缩小空间32倍

比如假设我们有N{2，3，64}个数中最大的是MAX，那么我们只需要开int[MAX/32+1]个int数组就可以存储完这些数据，具体可以看以下结构：

Int a : 0000 0000 0000 0000 0000 0000 0000 0000 这里是32个位置，我们可以利用每个位置的0或者1来表示该位置的数是否存在,这样我们就可以得到以下存储结构：

Data[0]: 0~31 32位
Data[1]: 32~63 32位
Data[2]: 64~95 32位
Data[MAX / 32+1]

/**
 * 解决：
 * 1. 数据去重
 * 2. 对没有重复的数据排序
 * 3. 根据1和2扩展其他应用，比如不重复的数，统计数据
 * 缺点： 数据不能重复、字符串hash冲突、数据跨多比较大的也不适合
 *
 * 求解2亿个数，判断某个数是否存在
 *
 * 最大的数是64  data[64/32] = 3
 * data[0] 0000 0000 0000 0000 0000 0000 0000 0000  0~31
 * data[1] 0000 0000 0000 0000 0000 0000 0000 0000  32~63
 * data[2] 0000 0000 0000 0000 0000 0000 0000 0000  64~95
 *
 *  数字 2 65 2亿分别位置
 *  2/32=0 说明放在data[0]数组位置， 2%32=2说明放在数组第3个位置
 *  65/32=2 说明放在data[2]数组位置， 65%32=1说明放在数组第2个位置
 *
 *  2亿=M
 *  开2亿个数组 2亿*4(byte) / 1024 /1024 = 762M
 *  如果用BitMap: 2亿*4(byte)/32 / 1024 /1024 = 762/32 = 23M  （int数组）
 *  判断66是否存在 66/32=2 -> 66%32=2 -> data[2]里面找第三个位置是否是1
 */
public class BitMap {

    byte[] bits; //如果是byte那就是只能存8个数
    int max; //最大的那个数

    public BitMap(int max) {
        this.max = max;
        this.bits = new byte[(max >> 3) + 1]; // max / 8 + 1
    }

    public void add(int n) { //添加数字
        int bitsIndex = n >> 3; // 除8就可以知道在哪一个byte
        int loc = n % 8; // n % 8 与运算可以标识求余 n & 8

        //接下来要把bit数组里面bitsIndex下标的byte里面第loc个bit位置设置为1
        // 0000 0100
        // 0000 1000
        // 或运算（|）
        // 0000 1100
        bits[bitsIndex] |= 1 << loc;
    }

    public boolean find(int n) {
        int bitsIndex = n >> 3;
        int loc = n % 8;

        int flag = bits[bitsIndex] & (1 << loc);

        if (flag == 0) {
            return false; //不存在
        } else {
            return true; //存在
        }
    }


    public static void main(String[] args) {
        BitMap bitMap = new BitMap(100);
        bitMap.add(2);
        bitMap.add(3);
        bitMap.add(65);
        bitMap.add(64);
        bitMap.add(99);

        System.out.println(bitMap.find(2));
        System.out.println(bitMap.find(5));
        System.out.println(bitMap.find(64));
    }
}

Set

各种容器对比

  • List：
    可以重复存储对象
    插入的顺序和遍历的顺序是一致的
    常用的实现方式：链表+数组（ArrayList,LinkedList,Vector）
  • Set：
    不允许重复对象
    无法保证每个元素的插入和输出顺序，无序容器。
    TreeSet是有序的
    常用的实现方式：HashSet，TreeSet，LinkedHashSet（强行保证输出顺序和插入顺序一致，双向链表，耗费空间）
  • Map：
    Map是键值对的形式存储，会有key+value：
    Map不允许出现相同的key，出现就会倍覆盖
    Map主要实现方式：HashMap，HashTable，TreeMap（也是一个有序的，默认按照自然顺序，其底层结构同样是红黑树）

布隆过滤器（不存在的就肯定不存在）

实现的思想：

  • 插入：将一个插入的元素使用K个hash函数进行k次计算，将得到的Hash值所对应的bit数组下标置为1
  • 查找：跟插入一样的道理，将查找的元素使用k个函数进行k次计算，将得到的值找出对应的bit数组下标，判断是否为1，如果都为1则说明这个值可能在序列中，反之肯定不在序列中

为什么是可能在序列中呢？存在误判率

  • 删除：非常明确的告诉你，这玩意是不支持删除的
/**
 * 应用场景 -- 允许一定误差率 0.1%
 * 1. 爬虫
 * 2. 缓存击穿 小数据量用hash或id可以用bitmap
 * 3. 垃圾邮件过滤
 * 4. 秒杀系统
 * 5. hbase.get
 */
public class BloomFilter {

    private int size;

    private BitSet bitSet;

    public BloomFilter(int size) {
        this.size = size;
        bitSet = new BitSet(size);
    }

    public void add(String key) {
        bitSet.set(hash_1(key), true);
        bitSet.set(hash_2(key), true);
        bitSet.set(hash_3(key), true);
    }

    public boolean find(String key) {
        if (bitSet.get(hash_1(key)) == false)
            return false;
        if (bitSet.get(hash_2(key)) == false)
            return false;
        if (bitSet.get(hash_3(key)) == false)
            return false;
        return true;
    }

    public int hash_1(String key) {
        int hash = 0;
        for (int i = 0; i < key.length(); ++i) {
            hash = 33 * hash + key.charAt(i);
        }
        return hash % size;
    }

    public int hash_2(String key) {
        int p = 16777169;
        int hash = (int) 2166136261L;
        for (int i = 0; i < key.length(); i++) {
            hash = (hash ^ key.length()) * p;
        }
        hash += hash << 13;
        hash ^= hash >> 7;
        hash += hash << 3;
        hash ^= hash >> 17;
        hash += hash << 5;
        return Math.abs(hash) % size;
    }

    public int hash_3(String key) {
        int hash, i;
        for (hash = 0, i = 0; i < key.length(); ++i) {
            hash += key.charAt(i);
            hash += (hash << 10);
            hash ^= (hash >> 6);
        }
        hash += (hash << 3);
        hash ^= (hash >> 11);
        hash += (hash << 15);
        return Math.abs(hash) % size;
    }

    public static void main(String[] args) {
        BloomFilter bloomFilter = new BloomFilter(Integer.MAX_VALUE);//21亿/8/1024/1024=250M
        System.out.println(bloomFilter.hash_1("1"));
        System.out.println(bloomFilter.hash_2("1"));
        System.out.println(bloomFilter.hash_3("1"));

        bloomFilter.add("1111");
        bloomFilter.add("1112");
        bloomFilter.add("1113");
        System.out.println(bloomFilter.find("1"));
        System.out.println(bloomFilter.find("1112"));
    }
}

Google Guava Test

<dependency>
    <groupId>com.google.guava</groupId>
    <artifactId>guava</artifactId> <!-- google bloomfilter 布隆过滤器 -->
    <version>22.0</version>
</dependency>

public class GoogleGuavaBloomFilterTest {
    public static void main(String[] args) {
        int dataSize = 1000000; //插入的数据N
        double fpp = 0.001; //0.1% 误判率

        BloomFilter<Integer> bloomFilter = BloomFilter.create(Funnels.integerFunnel(), dataSize, fpp);

        for (int i = 0; i < 1000000; i++) {
            bloomFilter.put(i);
        }

        //测试误判率
        int t = 0;
        for (int i = 2000000; i < 3000000; i++) {
            if (bloomFilter.mightContain(i)) {
                t++;
            }
        }
        System.out.println("误判个数：" + t);
    }
}

中文分词

Trie树

  1. 什么是Trie树：trie树就是我们平常说的字典树，它是一种专门用来处理字符串匹配的数据结构。特别适合用来在很多字符串中快速查找某一个特定的字符串。前缀树，赫夫曼树，前缀编码

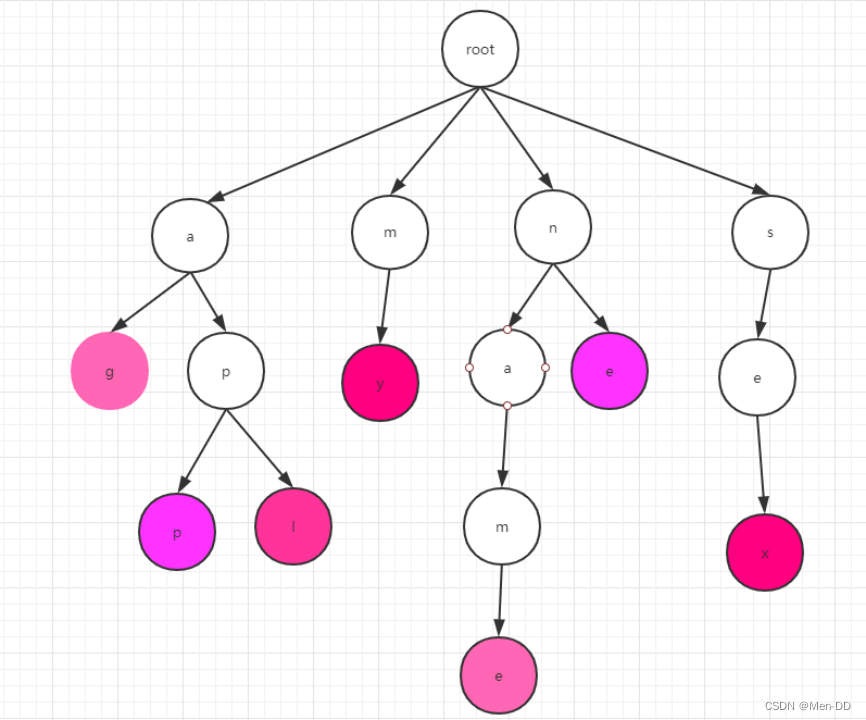
  2. Trie的数据结构：假设我们有以下几个英文单词：my name apple age sex，假如我们要查找里面某一个字符串是否存在，你怎么去找呢？利用字符串的公共前缀，将重复的合在一起组成一颗树，即为我们所要讲的trie树

  3. Trie树的构建：我们要先将词分成一个个的字母，然后再依次插入到树中。如右图所示，根节点root，如果我们要插入app
    则首先将app分成：a,p,p，然后从root点开始，一层层的插入，注意的是
    P会挂在a下面，后面的一个p会挂在前面的p上。单词的末尾我们就用紫色表示。
    这里需要注意我们插入的时候每一层的字母都是有序的。

  4. Trie的查找：
    查找我们就从root点开始，再第一层找第一个字母，依次往下找到我们所要的单词。
    注意要找到末尾的标记才算完成一个单词的查找。比如app，我们要找ap
    虽然字典树里面有ap，但是这个p不是紫色那么ap还是不存在字典树中的。

  5. Trie树的实现: Trie树是一颗多叉树。这里我们应该要想到B+Tree&B-Tree，是有些类似的。
    Trie树又是巧妙的利用了数组的下标，因为英文字母刚好是26个，所以我们可以开一个26长度的数组
    A[] = new int[26];
    A[0] = ‘a’ => 下标就是’a’-97 这里刚好就是0，利用的是ascii计算。
    所以它的数据结构应该是

class TrieNode {
  Char c;//存储当前这个字符
  TrieNode child[26] = new TrieNode[];//存储这个字符的子节点
}
  1. Trie树的分析：
  • 时间复杂度：非常高效 O(单词的长度)
  • 空间复杂度：以空间来换效率的数据结构。因为每个单词理论上都有26个子节点，所有它的空间复杂度就是26^n，n表示的是树的高度。
  • 优化：
    1. 重复的字母不要重复建
    2. 因为我们每个node都开了26个空间来存储节点。但实际情况可能不需要这么多，所以这里其实我们可以考虑用散列表来实现，
      这里大家可以去看IK的源码，当子节点少的时候是用的数组，但是节点大于3个是它是用的hashMap，这个再一定的程度上是可以节省很多的空间的。

在这里插入图片描述

中文分词

  1. 分词的原理：
    （1）英文分词：my name is WangLi
    （2）中文分词：我是中国人

  2. 中文分词器IK

  3. 中文分词需要特别注意的是它有两种方式：

    • Smart：智能分词，这里不会分出一句话的所有情况，比如我是中国人，会分成 我 / 是 /中国人
    • 最小颗粒（非Smart）：会分出一句话里面的所有情况，比如 我是中国人 会分成 我 / 是 / 中国 / 中国人 /国人

  4. 中文的歧义问题：利用词库，复杂的还会运用到AI技术 机器学习算法等
    武汉市长江大桥

    • 武汉市/长江大桥
    • 武汉/市长/江大桥

在这里插入图片描述

Lucene 倒排索引

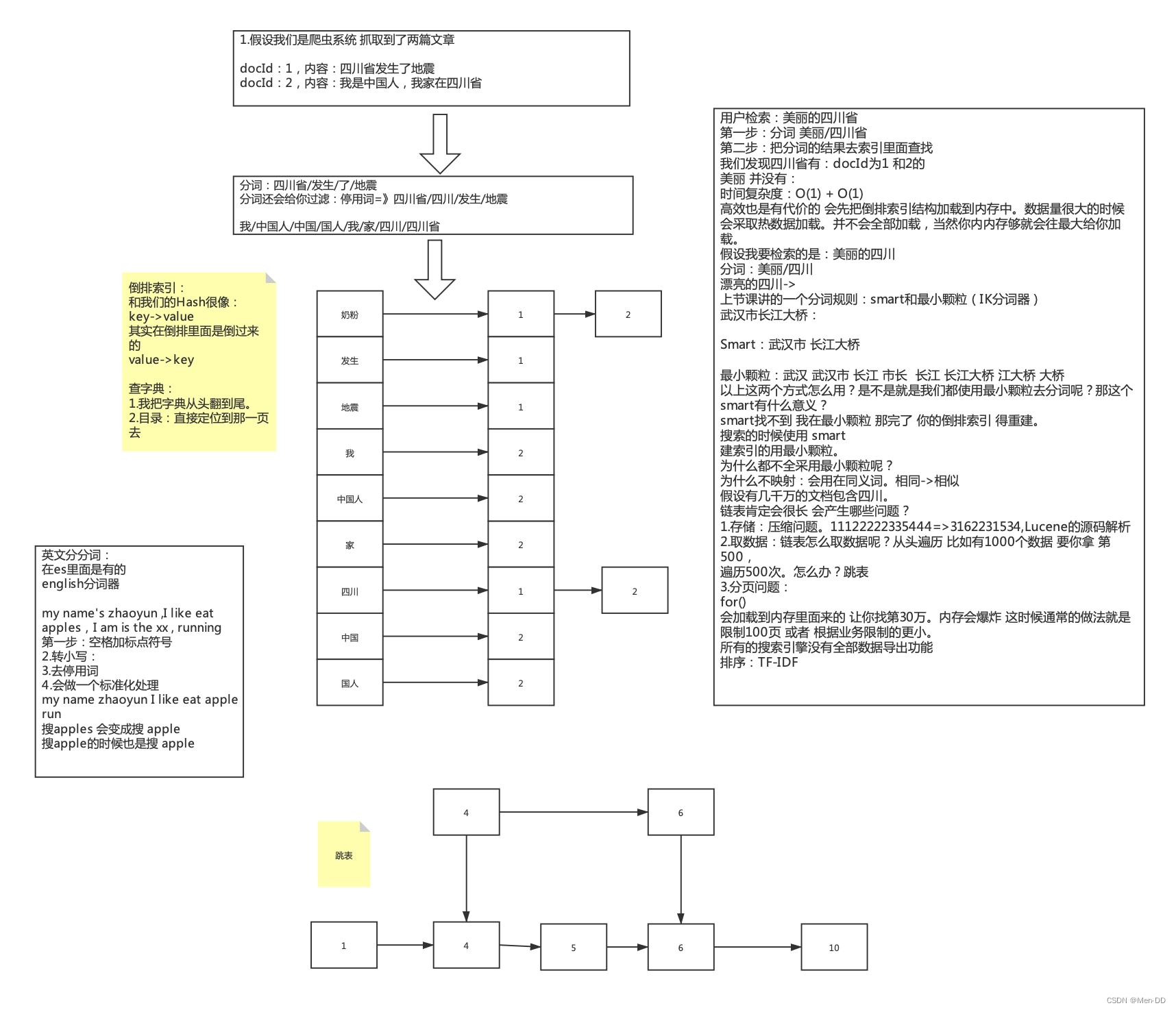
在这里插入图片描述

搜索引擎

  • 数据结构：数据结构在所有的文档中出现了多少次。如果有10篇文章，竟然都出现了数据结构。是不是就表示没有什么区分度

  • TF：词频 一篇doc中包含了多少这个词，包含越多表明越相关。只计算一篇文档的数量

  • DF：文档频率 包含这个词的文档总数，DF在一篇文档算一次

  • IDF：DF取反 也就是 1/DF;如果包含该词的文档越少，也就是DF越小，IDF越大，则说明词对这篇文档重要性就越大

  • TF-IDF: TF*IDF 的主要思想是：如果某个词或短语在一篇文章中出现的频率TF高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，这篇文章的得分也就越高。
    有什么问题？长度的有大有小，一篇文章就2个词，搜其中一个讲道理是50%的权重，有一篇文章有100个词，48词

  • 归一化处理：主要是对TF-IDF做处理，会根据文章的长度

  • 打分的定制加成

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/460849.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Ubuntu20.04+安装MySQL8+ 并设置忽略表名大小写

Ubuntu20.04+安装MySQL8+ 并设置忽略表名大小写

更新apt apt -y update安装mysql-server apt -y install mysql-server查看服务是否启动 ps -ef | grep mysql如下图启动成功 或者 systemctl status mysql设置root登录密码 执行命令&#xff1a; mysql -uroot选择数据库&#xff1a; use mysql;修改密码&#xff1a; a…
阅读更多...
0602基础使用（一）-react路由-react

0602基础使用（一）-react路由-react

文章目录 1 基本使用1.1 安装js库1.2 使用示例1.3 总结 2 路由组件与一般组件2.1 路由组件2.2 路由组件与普通组件示例2.3 总结 3 NavLink组件3.1 NavLink 简介3.2 NavLink实现高亮与自定义样式 结语 1 基本使用 1.1 安装js库 react-router-dom&#xff0c;react的一个插件库…
阅读更多...
flink on k8s提交任务

flink on k8s提交任务

目录 相关文档前置准备构建镜像提交任务 相关文档 https://nightlies.apache.org/flink/flink-docs-release-1.13/docs/deployment/resource-providers/native_kubernetes/ 前置准备 flink的lib目录下放入两个依赖 bcpkix-jdk15on-1.68.jar bcprov-jdk15on-1.69.jar 创建用户…
阅读更多...
Vue过滤器的基本使用

Vue过滤器的基本使用

过滤器 功能&#xff1a;对要显示的数据进行特定格式化后再显示 注意&#xff1a;并没有改变原本的数据&#xff0c;是产生新的对应的数据 声明&#xff1a;过滤器不是必须要用到的东西&#xff0c;而是vue提供处理数据的方式而已&#xff0c;想用就用&#xff0c;不想用可以…
阅读更多...
Elasticsearch 实战篇 | 黑马旅游

Elasticsearch 实战篇 | 黑马旅游

一、酒店搜索和分页 需求&#xff1a;实现黑马旅游的酒店搜索功能&#xff0c;完成关键字搜索和分页 1、定义实体类&#xff0c;接收前端的参数 如果当搜索条件为空的时候&#xff0c;就返回全部数据&#xff0c;不为空才按照key来搜索 二、条件过滤 修改实体类&#xff0c;…
阅读更多...
边缘计算开源项目解读-kubeedge metamanager实现

边缘计算开源项目解读-kubeedge metamanager实现

0 背景 笔者在前面的几篇文章从设备管理和运维的角度解读了kubeedge的相关代码流程和架构。本文将切入kubeedge edgecore的另一个核心业务&#xff0c;即边云协同处理设备元数据相关代码的解读。如果说前面的设备管理和运维并不能体现kubeedge作为边缘计算数据处理平台的特点&a…
阅读更多...
【Andoroid】之【APK瘦身】

【Andoroid】之【APK瘦身】

一、如何查看 APK 的组成 如果要优化 APK 的大小&#xff0c;我们首先需要知道我们编译出来的 APK 都包含哪些东西&#xff0c;然后针对占用大的做裁剪&#xff0c;或者删除不需要的东西&#xff0c;从而达到瘦身的目的。 查看 APK 的内容占用情况很简单&#xff0c;打开 AS …
阅读更多...
进程间通信，有名管道（pipe）与无名管道（fifo）的解析与运用，以及代码实现

进程间通信，有名管道（pipe）与无名管道（fifo）的解析与运用，以及代码实现

&#x1f38a;【进程通信与并发】专题正在持续更新中&#xff0c;进程&#xff0c;线程&#xff0c;IPC&#xff0c;线程池等的创建原理与运用✨&#xff0c;欢迎大家前往订阅本专题&#xff0c;获取更多详细信息哦&#x1f38f;&#x1f38f;&#x1f38f; &#x1fa94;本系列…
阅读更多...
API网关：开源Apinto网关-应用管理篇

API网关：开源Apinto网关-应用管理篇

需求痛点 在这互联网高速发展的时代&#xff0c;企业业务系统多、渠道广&#xff0c;如何管理内外部调用端系统具有极大的挑战。 数量方面&#xff1a;API网关需要对各端应用统一管理&#xff0c;例如对企业自身很多的前端应用&#xff0c;包括不限于web应用、移动APP、小程序&…
阅读更多...
AI边缘计算智能分析网关灭火器缺失检测与告警的实现过程

AI边缘计算智能分析网关灭火器缺失检测与告警的实现过程

AI智能分析网关基于边缘智能&#xff0c;部署了多种AI深度学习算法&#xff0c;可对接入的多路视频流进行智能检测、智能识别等&#xff0c;包括人脸检测与识别、车辆检测与识别、车牌识别、烟火识别、安全帽识别、区域入侵检测等。今天我们来介绍下关于灭火器缺失检测与告警的…
阅读更多...
基于Yolov5/Yolov7的DRConv动态区域感知卷积，即插即用，涨点显著！

基于Yolov5/Yolov7的DRConv动态区域感知卷积，即插即用，涨点显著！

1.Dynamic Region-Aware Convolution 论文：https://arxiv.org/pdf/2003.12243.pdf 本文提出了一种新的卷积算法，称为动态区域卷积算法（DRConv） ，该算法能够自动将滤波器分配到相应的空间区域，因此，DRConv具有强大的语义表示能力，并完美地保持了平移不变性。 DRConv的…
阅读更多...
在IIS7下使用ASP连接ACCESS数据库时提示如下错误的处理方法

在IIS7下使用ASP连接ACCESS数据库时提示如下错误的处理方法

“/”应用程序中的服务器错误。 未在本地计算机上注册“microsoft.jet.oledb.4.0”提供程序。 这是由于使用的Win2008系统是64位的&#xff0c;以前Win2003是32位。有以下两种解决方法&#xff1a; 1、修改连接数据库的代码&#xff1a; 如原代码是 DataPath "App_Data…
阅读更多...
Eclipse代码提示突然失灵的解决方案

Eclipse代码提示突然失灵的解决方案

不知道改动了啥&#xff0c;突然间Eclipse的代码提示就失效了&#xff0c;发现缺少后极不方便。 使用快捷键&#xff1a;Alt/ 提示 No Default Proposals 为什么使用快捷键&#xff1a;Alt/ 会提示“No Default Proposals。”呢&#xff1f; 网上提示可能是热键冲突 但是一套…
阅读更多...
可调直动差压卸荷阀DDRV-100、DBRV-100

可调直动差压卸荷阀DDRV-100、DBRV-100

优点&#xff1a; 及时响应压力变化。 低压升。 潜在调节&#xff08;抗震动&#xff09;。 调整位置可锁定。 铝制操作手柄和填料压盖。 坚硬化处理。 可调直动式卸荷阀 ZRV-63 0类 可调直动式卸荷阀 DRV2-080 系列8 可调直动式卸荷阀 DRV-080_*_H 系列8 直动可调式…
阅读更多...
微服务架构详解（一）

微服务架构详解（一）

目录 1.微服务简介 2.微服务技术选型 3.微服务核心组件 3.1.注册中心 3.1.1.注册中心对比 3.2.服务网关 3.2.1.主流API网关对比 3.3.分布式配置中心 3.4.服务容错&#xff08;服务熔断&#xff09; 3.5.负载均衡 3.5.1.负载均衡有好几种实现策略&#xff0c; 3…
阅读更多...
读取配置文件（properties、yaml）的八种方法

读取配置文件（properties、yaml）的八种方法

基础&#xff1a; 一、通过普通的I/O流读取配置文件(BufferedReader) 1、properties文件 2、测试类 public class TestReadProperties {Testpublic void IOReadProperties() throws IOException {// 把配置文件的内容封装进mapMap<String, Object> map new HashMap&l…
阅读更多...
视频可视化搭建项目，通过简单拖拽方式快速生产一个短视频

视频可视化搭建项目，通过简单拖拽方式快速生产一个短视频

一、开源项目简介 《视搭》是一个视频可视化搭建项目。您可以通过简单的拖拽方式快速生产一个短视频&#xff0c;使用方式就像易企秀或百度 H5 等 h5 搭建工具一样的简单。目前行业内罕有关于视频可视化搭建的开源项目&#xff0c;《视搭》是一个相对比较完整的开源项目&#…
阅读更多...
矿井下无人值守变电所电力监控系统的探讨与产品选型

矿井下无人值守变电所电力监控系统的探讨与产品选型

摘要&#xff1a;为了探讨井下无人值守变电所的电力监控系统技术&#xff0c;以西山煤电马兰矿为背景&#xff0c;详细阐述了井下无人值守变电所电力监控系统技术的各项基本参数&#xff0c;如额定工作电压及整机输入视在功率、交换机或监控分站的传输口、高压配电装置的传输口…
阅读更多...
（二）ElasticSearch 辅助工具 Kibana 介绍与安装

（二）ElasticSearch 辅助工具 Kibana 介绍与安装

1、什么是 kibana &#xff1f; Kibana 是一个针对Elasticsearch的开源分析及可视化平台&#xff0c;用来搜索、查看交互存储在Elasticsearch索引中的数据。使用Kibana&#xff0c;可以通过各种图表进行高级数据分析及展示。 Kibana让海量数据更容易理解。它操作简单&#xff…
阅读更多...
怎么使用chatgpt，GPT的使用方式解析

怎么使用chatgpt，GPT的使用方式解析

怎么使用Chatgpt&#xff1f;这是很多人心中的疑惑&#xff0c;更多的人只是听说过chatgpt的大名&#xff0c;但是具体连见都没见过gpt&#xff0c;那么接下来小编就来给大家详细的介绍一下吧。 一.了解chatgpt ChatGPT是一个由人工智能和自然语言处理技术构建的聊天机器人。通…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023