绪论
深度学习(Deep Learning)是近年来发展十分迅速的研究领域,并且在人工智能的很多子领域都取得了巨大的成功。从根源来讲,深度学习是机器学习的一个分支,是指一类问题以及解决这类问题的方法。
深度学习问题是一个机器学习问题,指从有限样例中通过算法总结出一般性的规律,并可以应用到新的未知数据上。比如,我们可以从一些历史病例的集合中总结出症状和疾病之间的规律.这样当有新的病人时,我们可以利用总结出来的规律,来判断这个病人得了什么疾病。
机器学习的三个基本要素
机器学习是从有限的观测数据中学习(或“猜测”)出具有一般性的规律,并可以将总结出来的规律推广应用到未观测样本上。机器学习方法可以粗略地分为三个基本要素:模型、学习准则、优化算法。
- 模型
对于一个机器学习任务,首先要确定其输入空间𝒳 和输出空间𝒴。不同机器学习任务的主要区别在于输出空间不同。在二分类问题中𝒴 = {+1, −1},在𝐶 分类问题中𝒴 = {1, 2, ⋯ , 𝐶},而在回归问题中𝒴 = ℝ。
输入空间𝒳 和输出空间𝒴 构成了一个样本空间。对于样本空间中的样本(𝒙, 𝑦) ∈ 𝒳 × 𝒴,假定𝒙 和𝑦 之间的关系可以通过一个未知的真实映射函数𝑦 =𝑔(𝒙) 来描述.机器学习的目标是找到一个模型来近映射函数𝑔 ∶ 𝒳 → 𝒴。似真实映射函数𝑔(𝒙) 。
假设空间ℱ 通常为一个参数化的函数族:
-
学习准则
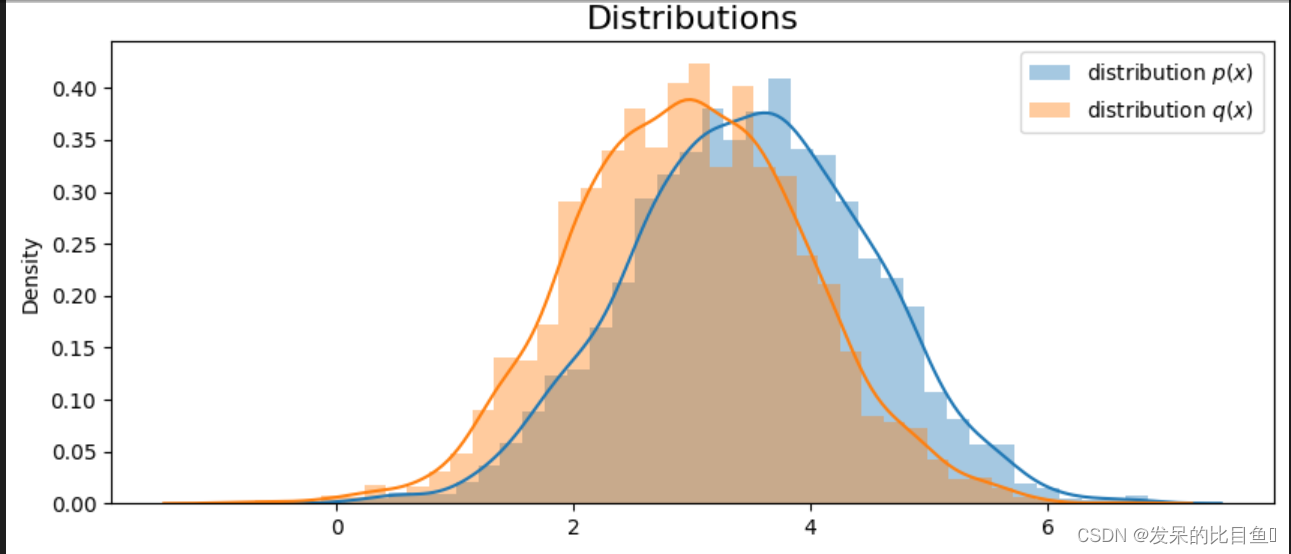
令训练集𝒟 = {(𝒙(𝑛), 𝑦(𝑛))}是由𝑁个独立同分布的(Independent and Identically Distributed,IID)样本组成,即每个样本(𝒙, 𝑦) ∈ 𝒳 × 𝒴 是从𝒳 和𝒴 的联合空间中按照某个未知分布𝑝𝑟(𝒙, 𝑦)独立地随机产生的。这里要求样本分布𝑝𝑟(𝒙, 𝑦)必须是固定的(虽然可以是未知的),不会随时间而变化。如果𝑝𝑟(𝒙, 𝑦)本身可变的话,就无法通过这些数据进行学习。
一个好的模型𝑓(𝒙, 𝜃∗) 应该在所有(𝒙, 𝑦) 的可能取值上都与真实映射函数𝑦 = 𝑔(𝒙) 一致,即|𝑓(𝒙, 𝜃∗) − 𝑦| < 𝜖, ∀(𝒙, 𝑦) ∈ 𝒳 × 𝒴,
其中𝜖是一个很小的正数。
2.1 损失函数
损失函数是一个非负实数函数,用来量化模型预测和真实标签之间的差异。下面介绍几种常用的损失函数。
0-1 损失函数
最直观的损失函数是模型在训练集上的错误率,即0-1 损失函数。
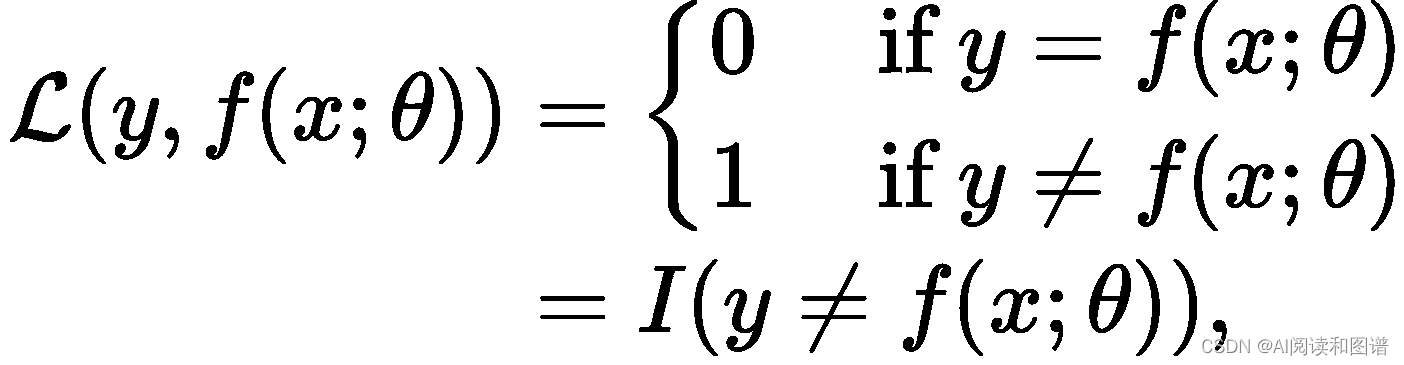
其中𝐼(⋅) 是指示函数。
虽然0-1 损失函数能够客观地评价模型的好坏,但其缺点是数学性质不是很好:不连续且导数为0,难以优化。因此经常用连续可微的损失函数替代。
平方损失函数
平方损失函数(Quadratic Loss Function)经常用在预测标签𝑦为实数值的任务中,定义为
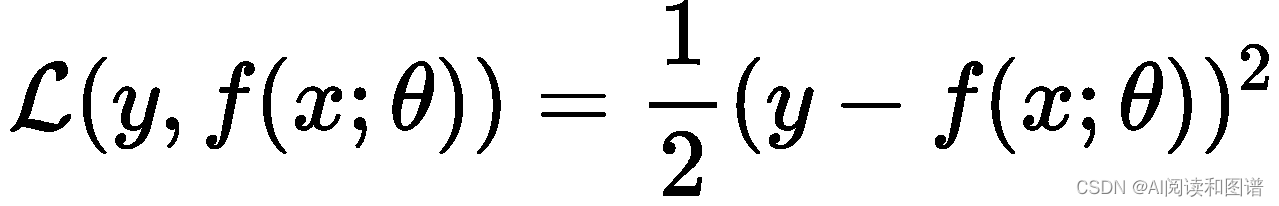
平方损失函数一般不适用于分类问题。
交叉熵损失函数
交叉熵损失函数(Cross-Entropy Loss Function)一般用于分类问题.假设样本的标签𝑦 ∈ {1, ⋯ , 𝐶} 为离散的类别,模型的输出为类别标签的条件概率分布,即
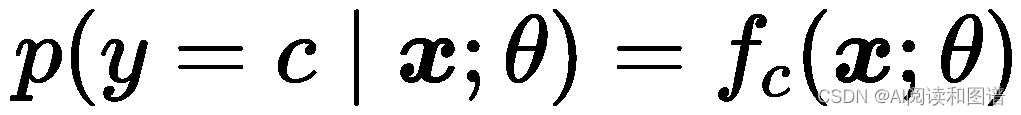
并满足
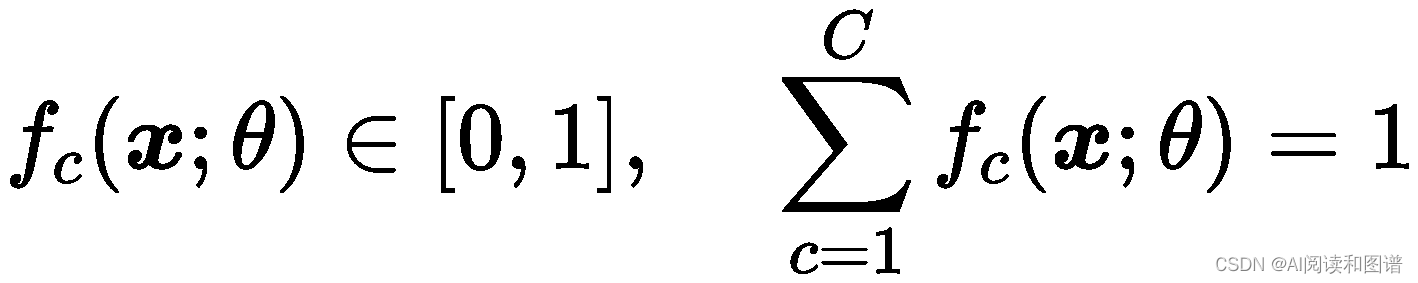
我们可以用一个𝐶 维的one-hot 向量𝒚 来表示样本标签.假设样本的标签为𝑘,那么标签向量𝒚 只有第𝑘 维的值为1,其余元素的值都为0.标签向量𝒚 可以看作样本标签的真实条件概率分布𝑝𝑟(𝑦|𝒙),),即第𝑐 维(记为𝑦𝑐,1 ≤ 𝑐 ≤ 𝐶)是类别为𝑐 的真实条件概率.假设样本的类别为𝑘,那么它属于第𝑘 类的概率为1,属于其他类的概率为0。
对于两个概率分布,一般可以用交叉熵来衡量它们的差异.标签的真实分布𝒚 和模型预测分布𝑓(𝒙; 𝜃) 之间的交叉熵为
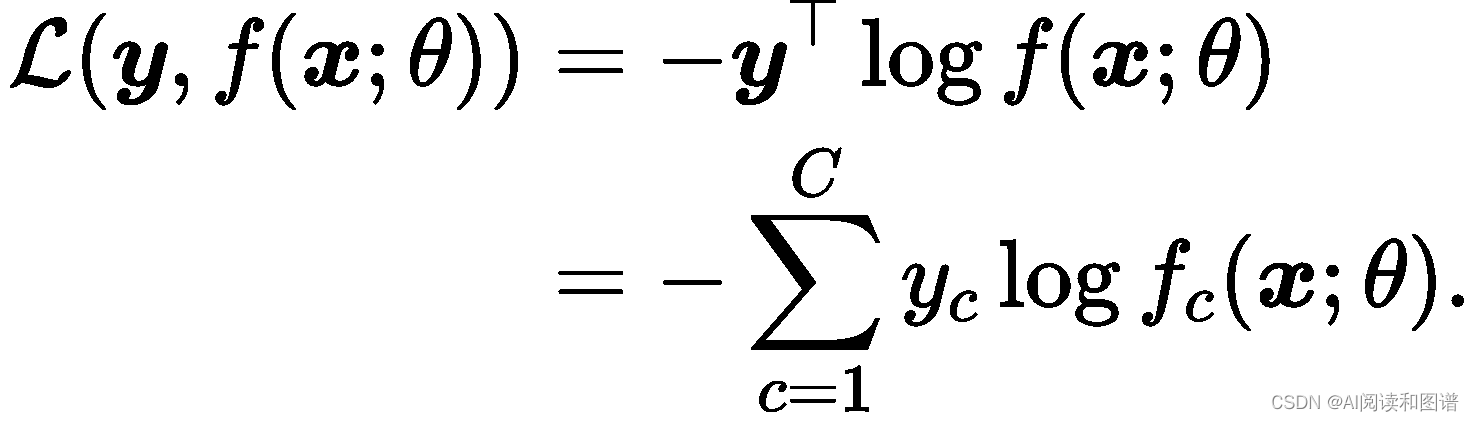
比如对于三分类问题,一个样本的标签向量为𝒚 = [0, 0, 1]T,模型预测的标签分布为𝑓(𝒙; 𝜃) = [0.3, 0.3, 0.4]T,则它们的交叉熵为−(0 × log(0.3) + 0 ×log(0.3) + 1 × log(0.4)) = − log(0.4).
因为𝒚 为one-hot 向量,上式也可以写为
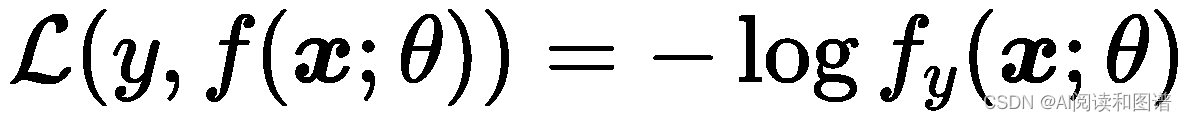
其中𝑓𝑦(𝒙; 𝜃) 可以看作真实类别𝑦 的似然函数.因此,交叉熵损失函数也就是负对数似然函数(Negative Log-Likelihood)。 -
优化算法
在确定了训练集𝒟、假设空间ℱ 以及学习准则后,如何找到最优的模型𝑓(𝒙, 𝜃∗) 就成了一个最优化(Optimization)问题.机器学习的训练过程其实就是最优化问题的求解过程。
参数与超参数
在机器学习中,优化又可以分为参数优化和超参数优化.模型𝑓(𝒙; 𝜃) 中的𝜃 称为模型的参数,可以通过优化算法进行学习.除了可学习的参数𝜃 之外,还有一类参数是用来定义模型结构或优化策略的,这类参数叫作超参数(Hyper-Parameter)。
常见的超参数包括:聚类算法中的类别个数、梯度下降法中的步长、正则化分布的参数。项的系数、神经网络的层数、支持向量机中的核函数等。超参数的选取一般都是组合优化问题,很难通过优化算法来自动学习。因此,超参数优化是机器学习的一个经验性很强的技术,通常是按照人的经验设定,或者通过搜索的方法对一组超参数组合进行不断试错调整。
3.1 梯度下降法
为了充分利用凸优化中一些高效、成熟的优化方法, 比如共轭梯度、拟牛顿法等,很多机器学习方法都倾向于选择合适的模型和损失函数,以构造一个凸函数作为优化目标。但也有很多模型(比如神经网络)的优化目标是非凸的,只能退而求其次找到局部最优解。
在机器学习中,最简单、常用的优化算法就是梯度下降法,即首先初始化参数𝜃0,然后按下面的迭代公式来计算训练集𝒟 上风险函数的最小值:
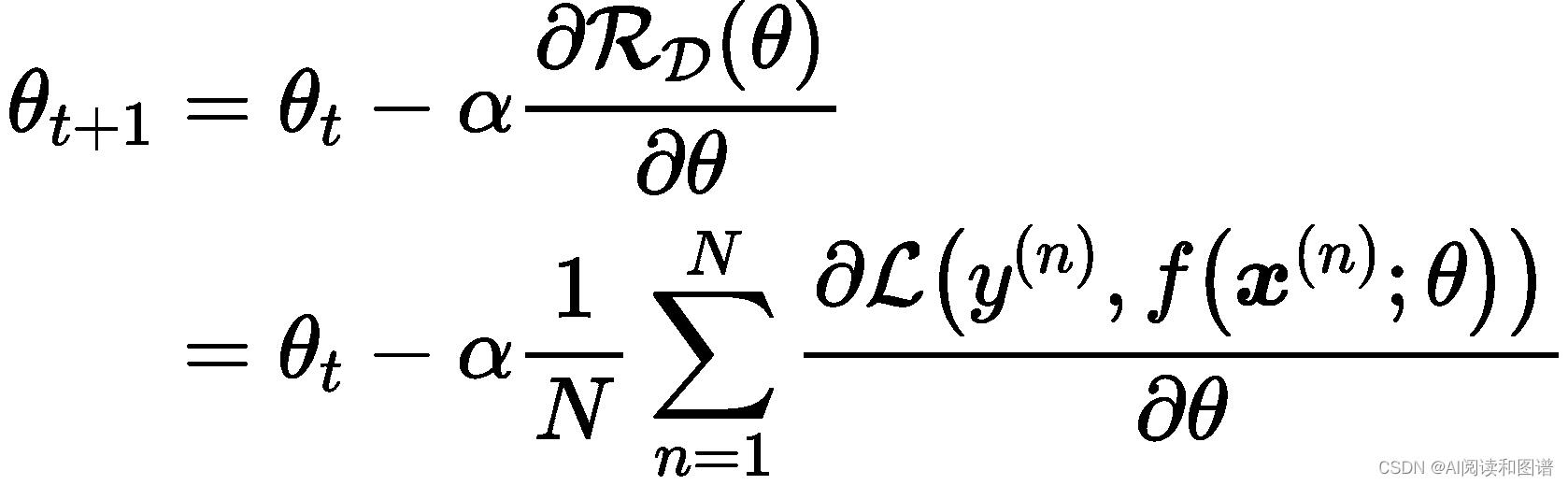
其中𝜃𝑡 为第𝑡 次迭代时的参数值,𝛼 为搜索步长.在机器学习中,𝛼 一般称为学习率(Learning Rate)。
3.2 提前停止
针对梯度下降的优化算法,除了加正则化项之外,还可以通过提前停止来防止过拟合。
在梯度下降训练的过程中,由于过拟合的原因,在训练样本上收敛的参数,并不一定在测试集上最优。因此,除了训练集和测试集之外,有时也会使用一个验证集(Validation Set)来进行模型选择,测试模型在验证集上是否最优。在每次迭代时,把新得到的模型𝑓(𝒙; 𝜃)在验证集上进行测试,并计算错误率。如果在验证集上的错误率不再下降,就停止迭代.这种策略叫提前停止(Early Stop).如果没有验证集,可以在训练集上划分出一个小比例的子集作为验证集.下图给出了提前停止的示例。
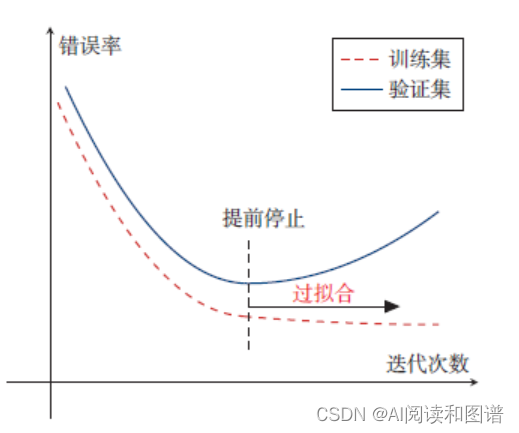
3.3 随机梯度下降法
在梯度下降法中,目标函数是整个训练集上的风险函数,这种方式称为批量梯度下降法(Batch Gradient Descent,BGD).批量梯度下降法在每次迭代时需要计算每个样本上损失函数的梯度并求和.当训练集中的样本数量𝑁 很大时,空间复杂度比较高,每次迭代的计算开销也很大。
在机器学习中,我们假设每个样本都是独立同分布地从真实数据分布中随机抽取出来的,真正的优化目标是期望风险最小.批量梯度下降法相当于是从真实数据分布中采集𝑁 个样本,并由它们计算出来的经验风险的梯度来近似期望风险的梯度.为了减少每次迭代的计算复杂度,我们也可以在每次迭代时只采集一个样本,计算这个样本损失函数的梯度并更新参数,即随机梯度下降法(Stochastic Gradient Descent,SGD)。当经过足够次数的迭代时,也可以收敛到局部最优解[Nemirovski et al., 2009]。
机器学习算法的类型
机器学习算法可以按照不同的标准来进行分类.比如按函数𝑓(𝒙; 𝜃) 的不同,机器学习算法可以分为线性模型和非线性模型;按照学习准则的不同,机器学习算法也可以分为统计方法和非统计方法。
但一般来说,我们会按照训练样本提供的信息以及反馈方式的不同,将机器学习算法分为以下几类:
监督学习
如果机器学习的目标是建模样本的特征𝒙 和标签𝑦 之间的关系:𝑦 = 𝑓(𝒙; 𝜃) 或𝑝(𝑦|𝒙; 𝜃),并且训练集中每个样本都有标签,那么这类机器学习称为监督学习(Supervised Learning)。根据标签类型的不同,监督学习又可以分为回归问题、分类问题和结构化学习问题。
(1) 回归(Regression)问题中的标签𝑦 是连续值(实数或连续整数),𝑓(𝒙; 𝜃) 的输出也是连续值。
(2) 分类(Classification)问题中的标签𝑦 是离散的类别(符号)。在分类问题中,学习到的模型也称为分类器(Classifier)。分类问题根据其类别数量又可分为二分类(Binary Classification)和多分类(Multi-class Classification)问题。
(3) 结构化学习(Structured Learning)问题是一种特殊的分类问题。在结构化学习中,标签𝒚 通常是结构化的对象,比如序列、树或图等。由于结构化学习的输出空间比较大,因此我们一般定义一个联合特征空间,将𝒙, 𝒚 映射为该空间中的联合特征向量𝜙(𝒙, 𝒚),预测模型可以写为
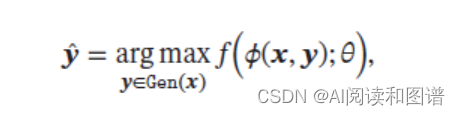 其中Gen(𝒙) 表示输入𝒙 的所有可能的输出目标集合.计算arg max 的过程也称为解码(Decoding)过程,一般通过动态规划的方法来计算。
其中Gen(𝒙) 表示输入𝒙 的所有可能的输出目标集合.计算arg max 的过程也称为解码(Decoding)过程,一般通过动态规划的方法来计算。
无监督学习
无监督学习(Unsupervised Learning,UL)是指从不包含目标标签的训练样本中自动学习到一些有价值的信息。典型的无监督学习问题有聚类、密度估计、特征学习、降维等。
强化学习
强化学习强化学习Reinforcement Learning,RL)是一类通过交互来学习的机器学习算法.在强化学习中,智能体根据环境的状态做出一个动作,并得到即
时或延时的奖励.智能体在和环境的交互中不断学习并调整策略,以取得最大化的期望总回报。
监督学习需要每个样本都有标签,而无监督学习则不需要标签。一般而言,监督学习通常需要大量的有标签数据集,这些数据集一般都需要由人工进行标
注,成本很高。因此,也出现了很多弱监督学习(Weakly Supervised Learning)和半监督学习(Semi-Supervised Learning,SSL)的方法,希望从大规模的无标注数据中充分挖掘有用的信息,降低对标注样本数量的要求。强化学习和监督学习的不同在于,强化学习不需要显式地以“输入/输出对”的方式给出训练样本,是一种在线的学习机制。
下图给出了三种机器学习类型的比较。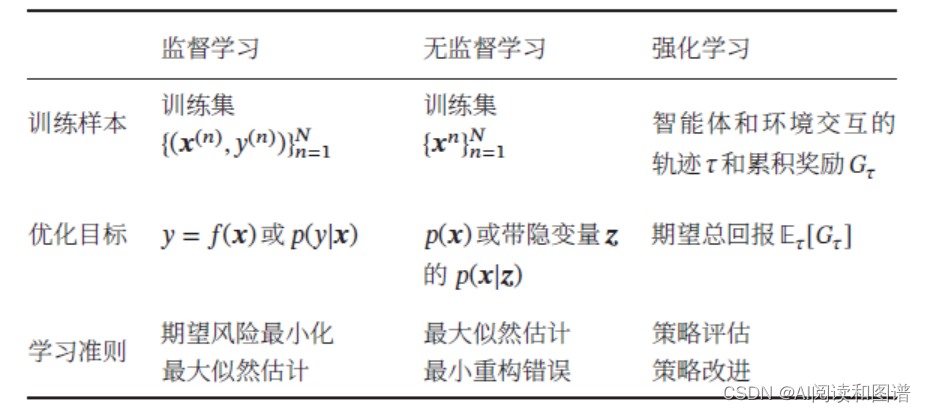
评价指标
为了衡量一个机器学习模型的好坏,需要给定一个测试集,用模型对测试集中的每一个样本进行预测,并根据预测结果计算评价分数。
对于分类问题,常见的评价标准有准确率、精确率、召回率和F 值等.给定测试集𝒯 ,假设标签𝑦(𝑛) ∈ {1, ⋯ , 𝐶},用学习好的模型𝑓(𝒙; 𝜃∗)对测试集中的每一个样本进行预测。
准确率
最常用的评价指标为准确率(Accuracy):
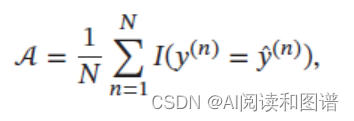
其中𝐼(⋅) 为指示函数。
错误率
和准确率相对应的就是错误率(Error Rate):
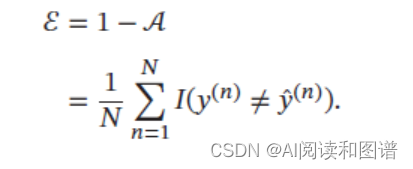
精确率和召回率
准确率是所有类别整体性能的平均,如果希望对每个类都进行性能估计,就需要计算精确率(Precision)和召回率(Recall)。精确率和召回率是广泛用于信息检索和统计学分类领域的两个度量值,在机器学习的评价中也被大量使用。
对于类别𝑐 来说,模型在测试集上的结果可以分为以下四种情况:
(1) 真正例(True Positive TP):一个样本的真实类别为𝑐 并且模型正确地预测为类别𝑐.这类样本数量记为
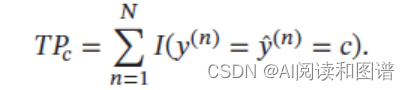
(2) 假负例(False Negative,FN):一个样本的真实类别为𝑐,模型错误地预测为其他类。这类样本数量记为
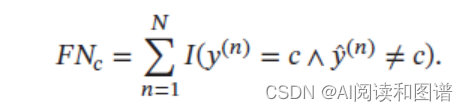
(3) 假正例(False Positive,FP):一个样本的真实类别为其他类,模型错误地预测为类别𝑐.这类样本数量记为
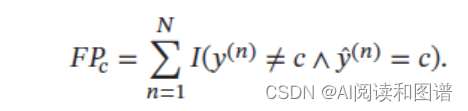
(4) 真负例(True Negative,TN):一个样本的真实类别为其他类,模型也预测为其他类.这类样本数量记为𝑇𝑁,对于类别𝑐 来说,这种情况一般不需要关注。
这四种情况的关系可以用如下所示的混淆矩阵(Confusion Matrix)来表示。

根据上面的定义,我们可以进一步定义查准率、查全率和F值。
精确率(Precision),也叫精度或查准率,类别𝑐 的查准率是所有预测为类别𝑐 的样本中预测正确的比例:

召回率(Recall),也叫查全率,类别𝑐 的查全率是所有真实标签为类别𝑐 的样本中预测正确的比例:
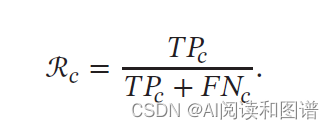
F 值(F Measure)是一个综合指标,为精确率和召回率的调和平均:
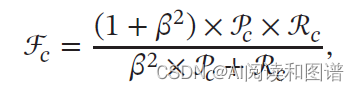
其中𝛽 用于平衡精确率和召回率的重要性,一般取值为1.𝛽 = 1 时的F 值称为F1值,是精确率和召回率的调和平均。
宏平均和微平均
宏平均和微平均
为了计算分类算法在所有类别上的总体精确率、召回率和F1值,经常使用两种平均方法,分别称为宏平均(Macro Average)和微平均(Micro Average)。
宏平均是每一类的性能指标的算术平均值:
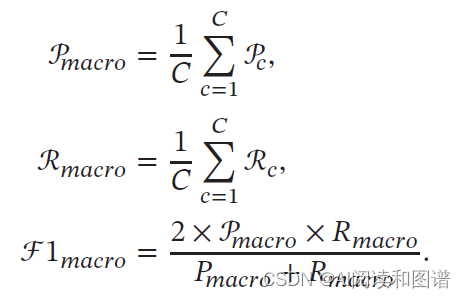
微平均是每一个样本的性能指标的算术平均值.对于单个样本而言,它的精确率和召回率是相同的(要么都是1,要么都是0)。因此精确率的微平均和召回率的微平均是相同的。同理,F1 值的微平均指标是相同的。当不同类别的样本数量不均衡时,使用宏平均会比微平均更合理些.宏平均会更关注小类别上的评价指标。
在实际应用中,我们也可以通过调整分类模型的阈值来进行更全面的评价, 比如AUC(Area Under Curve)、ROC(Receiver Operating Characteristic)曲线、PR(Precision-Recall)曲线等.此外,很多任务还有自己专门的评价方式,比如TopN 准确率。
交叉验证(Cross-Validation)是一种比较好的衡量机器学习模型的统计分析方法,可以有效避免划分训练集和测试集时的随机性对评价结果造成的影响。我们可以把原始数据集平均分为𝐾组不重复的子集,每次选𝐾 − 1组子集作为训练集,剩下的一组子集作为验证集。这样可以进行𝐾 次试验并得到𝐾 个模型,将这𝐾 个模型在各自验证集上的错误率的平均作为分类器的评价。
总结
本章简单地介绍了机器学习的基础知识,并为后面介绍的神经网络进行一些简单的铺垫.机器学习算法虽然种类繁多,但其中三个基本的要素为:模型、学习准则、优化算法.大部分的机器学习算法都可以看作这三个基本要素的不同组合.相同的模型也可以有不同的学习算法.比如线性分类模型有感知器、Logistic回归和支持向量机,它们之间的差异在于使用了不同的学习准则和优化算法。