基于异常值鲁棒性问题的极限学习机的回归问题研究（Matlab代码实现）

news2024/11/24 22:26:17

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

摘要：极限学习机( Extreme Learning Machine，ELM )作为机器学习中最有用的技术之一，由于其独特的超快学习能力而受到广泛关注。特别地，ELM在取得令人满意的结果的同时具有速度优势已被广泛认可。然而，异常值的存在可能导致不可靠的ELM模型。本文研究了ELM在回归问题中的异常值鲁棒性。基于异常值的稀疏特性，本文提出了一种基于1 -范数损失函数的异常值鲁棒性ELM来增强鲁棒性。特别地，采用快速准确的增广拉格朗日乘子法来保证算法的有效性和高效性。通过函数逼近实验和一些实际应用表明，该方法不仅保持了原始ELM的优点，而且在处理含有异常值的数据时表现出显著且稳定的精度。

近几十年来，特别是在大数据时代，用于机器学习和统计建模的数据集变得越来越大，并且很容易访问有关所研究现象的大量信息[1]。然而，由于数据采集过程中的人为或仪器错误，训练数据中可能会出现突出且远离其他常规样本的异常值[2]。因此，构建异常值鲁棒模型的要求随之而来，因为常规学习算法具有有利于异常值的自然倾向，这似乎大大降低了学习模型的准确性和可靠性。

Huang等人[3]提出的极限学习机（ELM）因其独特的特点和显著的性能[4]而是一种有效且高效的学习方法。ELM的优点归因于以下功能：（i）与大多数神经网络一样，ELM不仅具有近似嵌入大量训练数据中的未知函数的能力，而且还具有并行结构，以便在训练期间以及测试过程中执行快速高效的并行计算。（ii）大量实证研究表明，ELM往往比传统的SVM具有更好的可扩展性和泛化性能[3]，[5]。（iii）ELM以极快的学习速度执行，而其他传统学习算法必须面对高计算成本的挑战性问题。更准确地说，这是主要的优点，因为所有隐藏节点参数（输入权重和偏差）都是随机生成的（甚至在ELM看到训练数据之前），无需调整，因此可以分析确定输出权重。凭借这些非凡的优点，ELM在广泛的领域引起了广泛的关注。特别是对于回归问题，ELM已广泛应用于许多实际工程应用，例如电价预测[6]，股票市场预测[7]，[8]和铁磁材料的磁导率预测[9]。

尽管 ELM 具有许多优点，但有人指出，ELM 往往会受到训练数据中异常值的影响，这在处理实际应用程序时可能会发生 [10]。据我们所知，在强调ELM的异常稳健性方面做得很少。Huang等人[5]在原始ELM的基础上提出了正则化ELM，并规定输出权重的规范作为正则化项，对最终性能起着重要作用。邓等. [11] 通过结合加权最小二乘方案和正则化 ELM 提出了加权正则化 ELM。他们的工作在异常鲁棒性问题上显示出有希望的结果。霍拉塔等. [10]提出了迭代加权的ELM，然而，由于缺乏正则化项，性能并不理想，并且计算量大大增加，因为每次迭代涉及的时间与原始ELM所花费的时间一样多。所有这些方法都使用以l2-范数（或平方和）标准来学习模型。然而，有人指出，在2-范数容易受到异常值的严重影响，因为 l2-范数放大了与大偏差相关的异常值的影响[12]。通常，ELM模型具有l2-范数损失函数在存在异常值时往往不稳定。

在本文中，我们提出了一种新型ELM，其l1-异常值鲁棒性问题的范数损失函数。我们使用l 的原因1-范数而不是 l2-规范包括两折。一、1-范数对非典型观测值比 L 更稳健2-范数和l1范数损失函数已被广泛用于处理异常值（例如，参见[13]，[14]，[15]，[16]）。其次，稀疏性很突出，因为异常值通常只占整个训练样本的一小部分。压缩感知[17]，[18]，[19]，[20]和鲁棒主成分分析[21]，[22]两个研究领域的最新进展从理论上表明，在一定条件下，稀疏性可以通过1-规范。为了解决由此产生的优化问题，我们利用增强拉格朗日乘子（ALM）方法[23]来实现。虽然这种方法通常与迭代方案相关联，但事实证明，每次迭代中的简单公式使计算非常快，以实现有效的实现和竞争比较。考虑到我们提出的方法可以被视为异常鲁棒性问题的特殊ELM，为了简单起见，我们将其称为ORELM。

📚2 运行结果

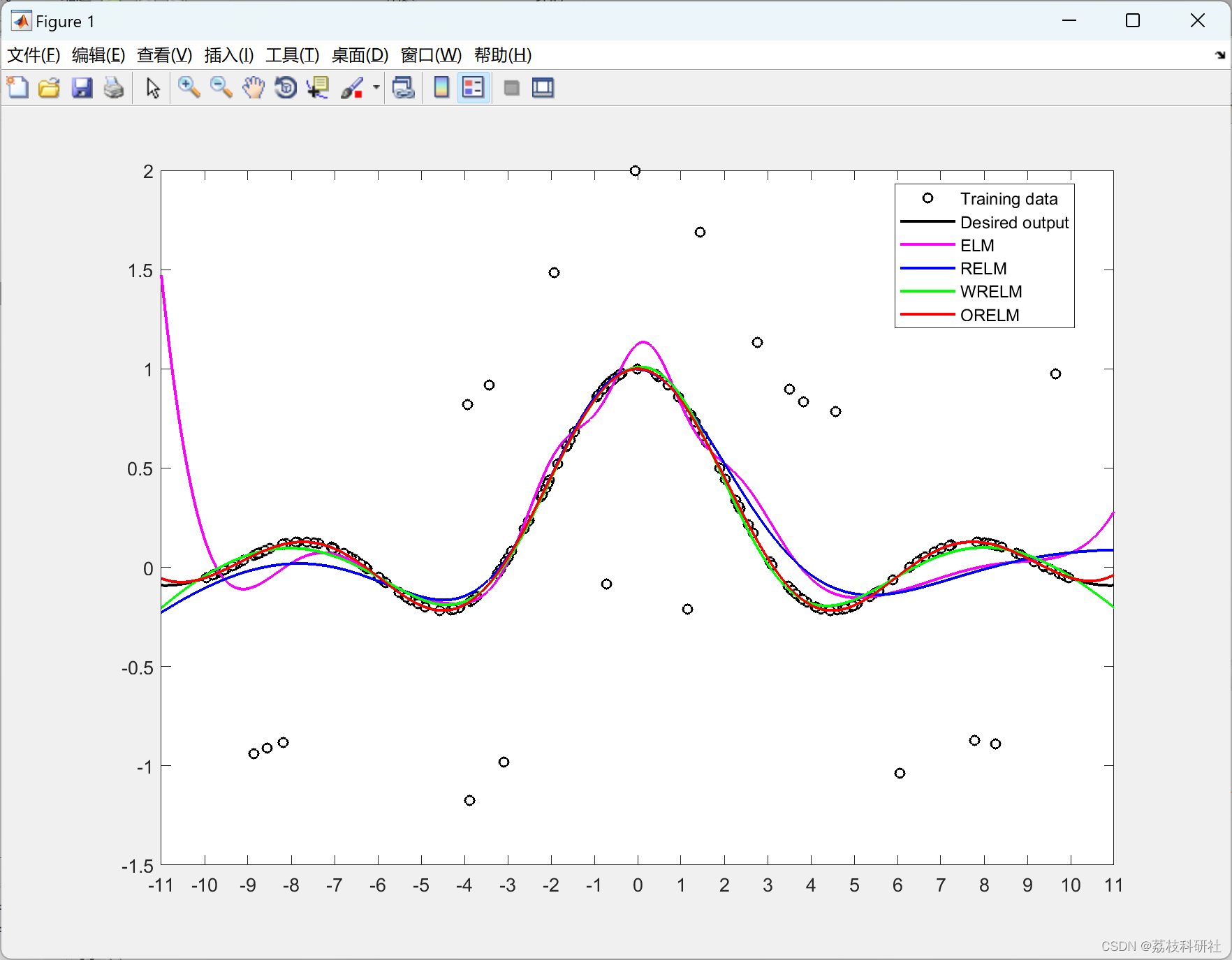
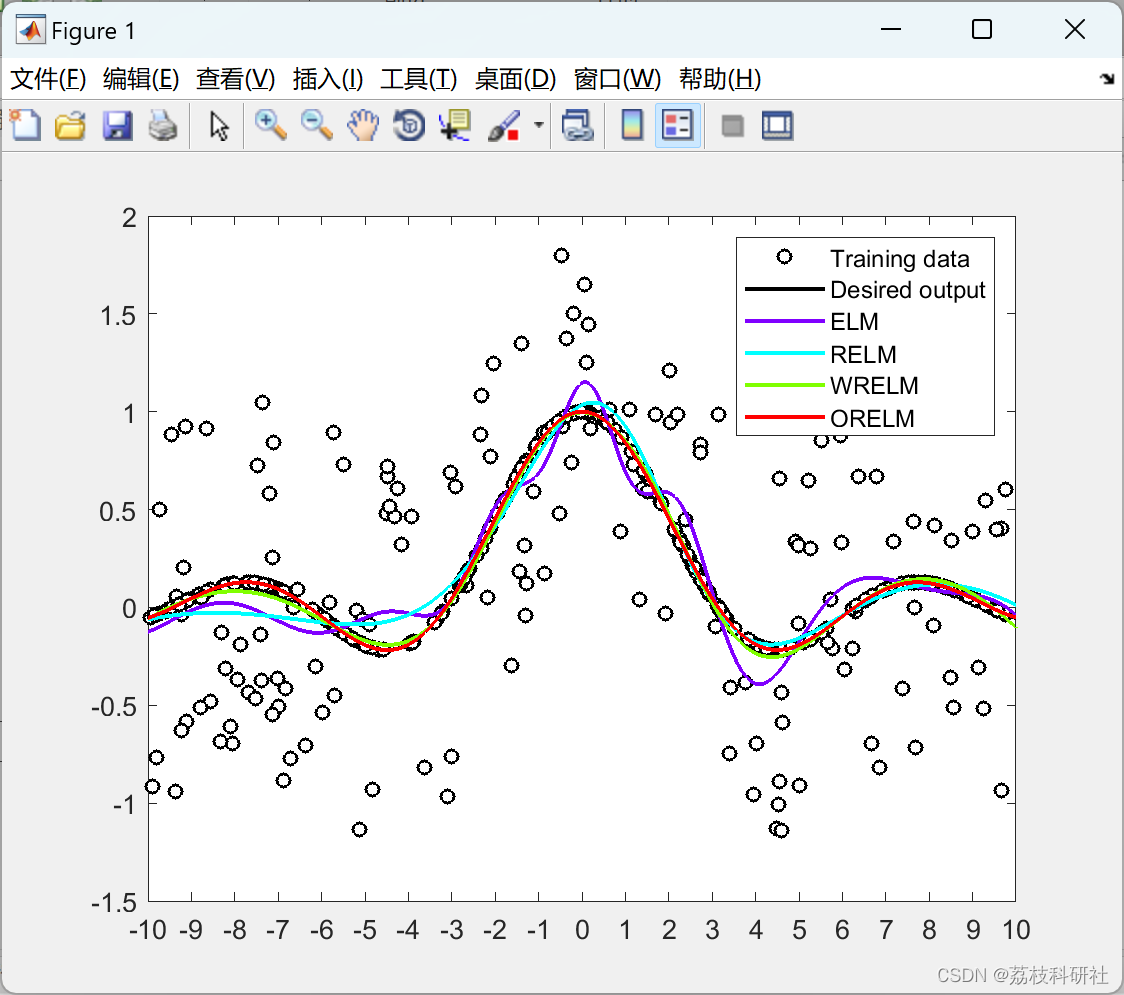
部分代码：

function [TestingAccuracy,TY] = elm_predict(TP,TT,InputWeight, BiasofHiddenNeurons, OutputWeight)

%%%%%%%%%%% Load testing dataset

NumberofTestingData=size(TP,2);

%load elm_model.mat;

%%%%%%%%%%% Calculate the output of testing input

tempH_test=InputWeight*TP;
clear TP; % Release input of testing data
ind=ones(1,NumberofTestingData);
BiasMatrix=BiasofHiddenNeurons(:,ind); % Extend the bias matrix BiasofHiddenNeurons to match the demention of H
tempH_test=tempH_test + BiasMatrix;

H_test = 1 ./ (1 + exp(-tempH_test));

TY=(H_test' * OutputWeight)'; % TY: the actual output of the testing data

TestingAccuracy=sqrt(mse(TT - TY)) ; % Calculate testing accuracy (RMSE) for regression case
% sum(sign(TY)==TV.T)/NumberofTestingData

%save('elm_output','TY');