7-11 互评成绩
学生互评作业的简单规则是这样定的:每个人的作业会被k个同学评审,得到k个成绩。系统需要去掉一个最高分和一个最低分,将剩下的分数取平均,就得到这个学生的最后成绩。本题就要求你编写这个互评系统的算分模块。
输入格式:
输入第一行给出3个正整数N(3 < N ≤104,学生总数)、k(3 ≤ k ≤ 10,每份作业的评审数)、M(≤ 20,需要输出的学生数)。随后N行,每行给出一份作业得到的k个评审成绩(在区间[0, 100]内),其间以空格分隔。
输出格式:
按非递减顺序输出最后得分最高的M个成绩,保留小数点后3位。分数间有1个空格,行首尾不得有多余空格。
输入样例:
6 5 3
88 90 85 99 60
67 60 80 76 70
90 93 96 99 99
78 65 77 70 72
88 88 88 88 88
55 55 55 55 55
输出样例:
87.667 88.000 96.000#include<bits/stdc++.h>
using namespace std;
int N, K, M;
vector<double> ans;
int main()
{
cin >> N >> K >> M;
while (N--)
{
double sum = 0;
vector<double>num(K);
for (int i = 0; i < K; i++)
{
cin >> num[i];
}
sort(num.begin(), num.end());
for (int i = 1; i < K - 1; i++)sum += num[i];
sum /= (K - 2);
ans.emplace_back(sum);
}
sort(ans.begin(), ans.end());
for (int i = ans.size() - M; i < ans.size(); i++)
{
printf("%.3lf",ans[i]);
if (i != ans.size()-1)cout << " ";
}
return 0;
}
7-10 列车调度
火车站的列车调度铁轨的结构如下图所示。
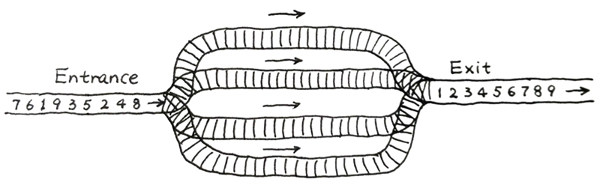
两端分别是一条入口(Entrance)轨道和一条出口(Exit)轨道,它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入,最后从出口离开。在图中有9趟列车,在入口处按照{8,4,2,5,3,9,1,6,7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开,则至少需要多少条平行铁轨用于调度?
输入格式:
输入第一行给出一个整数N (2 ≤ N ≤105),下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。
输出格式:
在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。
输入样例:
9
8 4 2 5 3 9 1 6 7
输出样例:
4#include<bits/stdc++.h>
using namespace std;
//我的解 === 查队列查尾巴 == 查找超时
vector<int> Q;
int N, num;//所需要的铁轨数
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> N;
while (N--)
{
cin >> num;
bool falg = false;//判断是否入队
for (int i = 0; i < Q.size(); i++)
{
if (Q[i] > num)
{
Q[i] = num;//更新队尾
falg = 1;
break;
}
}
if(!falg) Q.emplace_back(num);
}
cout << Q.size();
return 0;
}优化
通过二分查找减少时间
#include<bits/stdc++.h>
using namespace std;
//优化
vector<int> Q;
int N, num;//所需要的铁轨数
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> N;
while (N--)
{
cin >> num;
auto pos = lower_bound(Q.begin(),Q.end(),num);//返回第一个小于num的迭代器位置
if(pos == Q.end())
{
Q.emplace_back(num);
}
else
{
int X = pos - Q.begin();
Q[X] = num;//更新队尾
}
}
cout << Q.size();
return 0;
}
7-9 红色警报
战争中保持各个城市间的连通性非常重要。本题要求你编写一个报警程序,当失去一个城市导致国家被分裂为多个无法连通的区域时,就发出红色警报。注意:若该国本来就不完全连通,是分裂的k个区域,而失去一个城市并不改变其他城市之间的连通性,则不要发出警报。
输入格式:
输入在第一行给出两个整数N(0 < N ≤ 500)和M(≤ 5000),分别为城市个数(于是默认城市从0到N-1编号)和连接两城市的通路条数。随后M行,每行给出一条通路所连接的两个城市的编号,其间以1个空格分隔。在城市信息之后给出被攻占的信息,即一个正整数K和随后的K个被攻占的城市的编号。
注意:输入保证给出的被攻占的城市编号都是合法的且无重复,但并不保证给出的通路没有重复。
输出格式:
对每个被攻占的城市,如果它会改变整个国家的连通性,则输出Red Alert: City k is lost!,其中k是该城市的编号;否则只输出City k is lost.即可。如果该国失去了最后一个城市,则增加一行输出Game Over.。
输入样例:
5 4
0 1
1 3
3 0
0 4
5
1 2 0 4 3
输出样例:
City 1 is lost.
City 2 is lost.
Red Alert: City 0 is lost!
City 4 is lost.
City 3 is lost.
Game Over.#include<bits/stdc++.h>
using namespace std;
const int MAX = 510;
int N,M,K;
//并查集
bool MAP[MAX][MAX];
vector<bool>vis(MAX,0);
void dfs(int x)
{//意义:遍历搜索x的连通块
vis[x] = 1;//标记已被记录过来
for(int i = 0;i < N;i++)
{
if(!vis[i] && MAP[i][x])//若该点未被访问且和x有连通
dfs(i);
}
}
int AS_sum()
{//计算连通集合个数
int sum = 0;
for(auto i : vis) i = 0;
for(int i = 0;i<N;i++)
{
if(!vis[i])
{
dfs(i);
sum++;
}
}
return sum;
}
int main()
{
cin>>N>>M;
while(M--)
{
int A,B;
cin>>A>>B;
MAP[A][B] = MAP[B][A] = 1;
}
cin>>M;
int m = M;
int S = AS_sum();
while(M--)
{
cin>>K;//被攻陷的城市
for(int i = 0;i<N;i++)
{
if(MAP[i][K])
{
MAP[i][K] = MAP[K][i] = 0;//删除该城市的一切联系
}
}
int T = AS_sum();//重新判断连通集合数
if(T - 1 > S)
{//如果出现分裂的情况,那么集合块一定多出2块 例如: 1-2-3 断1 变成 1 和 2-3 连通性没有改变,若断2 变成 1 2 3 多出2块
printf("Red Alert: City %d is lost!\n",K);
}
else
{
printf("City %d is lost.\n",K);
}
S = T; // 每次都要更新最新的的集合块
//否则可能出现 初始为 1-2-3 4 集合块为2
//去 4 1-2-3 //此时集合块变成1 但是没有关系到整体的连通性,集合没有发生更新导致下列判断出现问题
//去 2 1 2 3 3 - 1 不满足 > 2
}
if(m == N)cout<<"Game Over."<<endl;
return 0;
}