回溯法（Java）

---

---

1、引言

迷宫问题中的回溯主要体现在当没有路可走时，会退回到上一个岔路口，重新在没有走过的路线中找一个没有走过的路走

• 理论上

寻找问题的解的一种可靠的方法是首先列出所有候选解，然后依次检查每一个，在检查完所有或部分候选解后，即可找到所需要的解。

• 事实上

1.当候选解数量有限并且通过检查所有或部分候选解能够得到所需解时，上述方法是可行的。

2.若候选解的数量非常大（指数级，大数阶乘），即便采用最快的计算机也只能解决规模很小的问题。

回溯和分支限界法是比较常用的对候选解进行系统检查两种方法。

• 按照这两种方法对候选解进行系统检查通常会使问题的求解时间大大减少（无论对于最坏情形还是对于一般情形） 。

• 可以避免对很大的候选解集合进行检查，同时能够保证算法运行结束时可以找到所需要的解。

• 通常能够用来求解规模很大的问题。

2、回溯法

2.1 定义

回溯法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就「回溯」返回，尝试别的路径。

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为「回溯点」。

以深度优先的方式系统地搜索问题的解的算法称为回溯法

2.2 使用场合

• 对于许多问题，当需要找出它的解的集合或者要求回答什么解是满足某些约束条件的最佳解时，往往要使用回溯法。

• 这种方法适用于解一些组合数相当大的问题，具有「通用解题法」之称。

2.3 基本做法

基本做法是搜索，或是一种组织得井井有条的，能避免不必要搜索的穷举式搜索法。

2.4 具体做法

系统性

回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。

跳跃性

算法搜索至解空间树的任意一点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对该结点为根的子树的搜索，逐层向其祖先结点回溯；否则，进入该子树，继续按深度优先策略搜索。

2.5 常见例子

图的深度优先遍历

3、比较

回溯法与穷举查找是一样的吗？

• 相同点

可以把回溯法和分支限界法看成是穷举法的一个改进。该方法至少可以对某些组合难题的较大实例求解。

• 不同点

每次只构造侯选解的一个部分。然后评估这个部分构造解：如果加上剩余的分量也不可能求得一个解，就绝对不会生成剩下的分量

4、 问题的解空间

4.1 介绍

• 问题的解向量

回溯法希望一个问题的解能够表示成一个n元式(x₁,x₂,…,x_n)的形式。

• 显约束

对分量x_i的取值范围的限定。

• 隐约束

为满足问题的解而对不同分量之间施加的约束。

4.2 解空间（Solution Space）

对于问题的一个实例，解向量满足显式约束条件的所有多元组，构成了该实例的一个解空间。

注意：同一问题可有多种表示，有些表示更简单，所需状态空间更小（存储量少，搜索方法简单）。

4.3 举例

对于有n种可选物品的0-1背包问题

• 解空间由2n个长度为n的0-1向量组成
• n=3时，解空间为{(0,0,0),(0,0,1),(0,1,0),(0,1,1), (1,0,0),(1,0,1),(1,1,0),(1,1,1)}

用完全二叉树表示的解空间

• 边上的数字给出了向量x中第i个分量的值x_i
• 根节点到叶节点的路径定义了解问题的一个解

5、基本思想

5.1 基本步骤

• 针对所给问题，定义问题的解空间；

• 确定易于搜索的解空间结构；

• 以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。

5.2 常用剪枝函数

• 用约束函数在扩展结点处剪去不满足约束的子树；

• 用限界函数剪去得不到最优解的子树。

5.3 深度优先的问题状态生成法

• 如果对一个扩展结点R，一旦产生了它的一个儿子C，就把C当做新的扩展结点。

• 在完成对子树C（以C为根的子树）的穷尽搜索之后，将R重新变成扩展结点，继续生成R的下一个儿子（如果存在）。

5.4 宽度优先的问题状态生成法

• 一个扩展结点变成死结点之前，它一直是扩展结点。

6、计算复杂性

• 空间复杂性

• 用回溯法解题的一个显著特征是在搜索过程中「动态产生问题的解空间」。在任何时刻，算法只保存从根结点到当前扩展结点的路径。

• 如果解空间树中从根结点到叶结点的最长路径的长度为h(n)，则回溯法所需的计算空间通常为O(h(n))。

• 显式地存储整个解空间则需要O(2h(n)或O(h(n)!)内存空间。

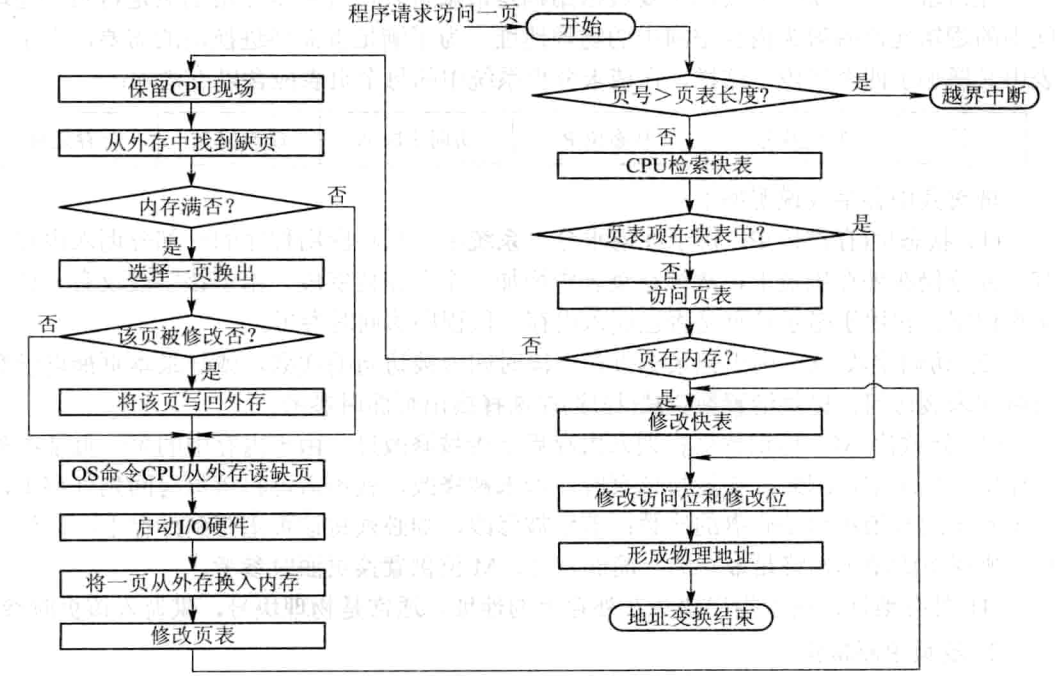
7、算法框架

如下图所示：

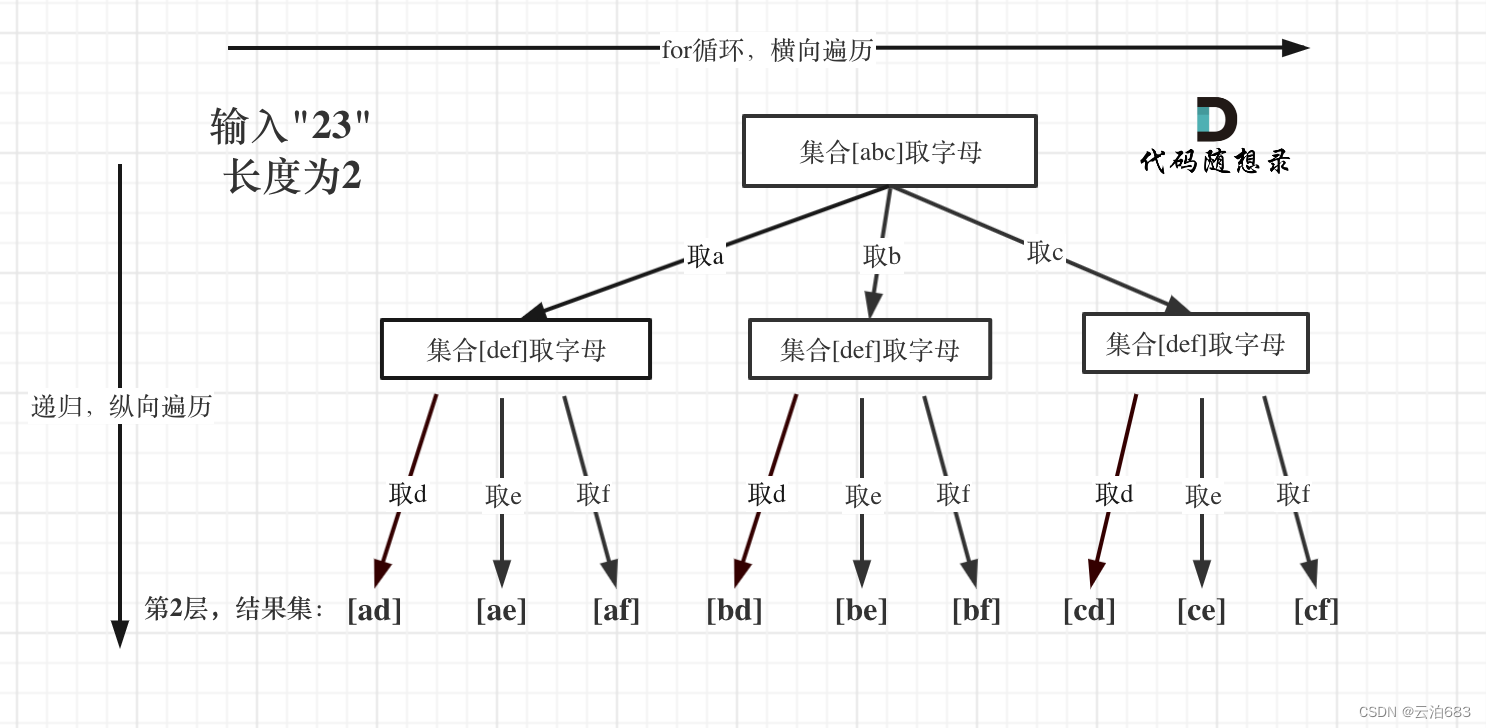
解空间一般用解空间树（Solution Space Trees,也称状态空间树）的方式组织，树的根结点位于第1层，表示搜索的初始状态，第2层的结点表示对解向量的第一个分量做出选择后到达的状态，第1层到第2层的边上标出对第一个分量选择的结果，依此类推，从树的根结点到叶子结点的路径就构成了解空间的一个可能解。

用完全二叉树表示的解空间(n=3)

左边子树表示1号物品要放入背包 ，右边子树表示1号物品不放入背包
树中的8个叶子结点分别代表该问题的8个可能解。

例如，从跟结点到结点H的路径相应于解空间中元素（1,1,1）

又如：

当搜索到一个L结点时，就把这个L结点变成为E结点，继续向下搜索这个结点的儿子结点。当搜索到一个D结点，而还未得到问题的最终解时，就向上回溯到它的父亲结点。如果这个父亲结点当前还是E结点，就继续搜索这个父亲结点的另一个儿子结点；如果这个父亲结点随着所有儿子结点都已搜索完毕而变成D结点，就沿着这个父结点向上，回溯到它的祖父结点。这个过程继续进行，直到找到满足问题的最终解。

8、核心代码

递归回溯

回溯法对解空间作深度优先搜索，因此，在一般情况下用递归方法实现回溯法，t表示搜索深度。

void backtrack (int t){
    if (t >n ) {         //t>n表示算法已搜索到叶节点
        output(x);     //记录或输出得到的可行解x
    } else {
        for (int i = f(n, t); i <= g(n, t); i++) {
            //其中f(n,t),g(n,t)分别表示在当前扩展结点处未搜索过的子树的起始编号和终止编号。
            x[t] = h(i);    //h(i)表示在当前扩展节点处x[t]的第i个可选值
            if (constraint(t) && bound(t))
                backtrack(t + 1);
        }
    }
}

if (Constraint(t)&&Bound(t) ) backtrack(t + 1)；

if语句含义：Constraint(t)和Bound(t)表示当前扩展节点处的约束函数和限界函数。

• Constraint(t): 返回值为true时，在当前扩展节点处x[1:t]的取值满足问题的约束条件，否则不满足问题的约束条件，可剪去相应的子树

• Bound(t): 返回的值为true时，在当前扩展节点处x[1：t]的取值为目标函数不越界，还需由backtrack(t+1)对其相应的子树做进一步搜索。否则，当前扩展节点处x[1：t]的取值是目标函数越界，可剪去相应的子树

• 递归出口：backtrack(t)执行完毕，返回t-1层继续执行，对还没有测试过的x[t-1]的值继续搜索。当t=1时，若以测试完x[1]的所有可选值，外层调用就全部结束。

迭代回溯

采用树的非递归深度优先遍历算法，可将回溯法表示为一个非递归迭代过程。

void iterativeBacktrack(){
    int t =1 ;
    while(t > 0) {
        if (f(n,t)< = g(n,t)) {
            for(int i = f(n,t); i <= g(n,t); i++) {
                x[t] = h(i);
                if (constraint(t) && bound(t)) {
                    if (solution(t)) {
                        output(x);   //输出最优解
                    } else {
                        t++;    //搜索下一层节点
                    }
                }
            }
        } else {
            t--;    //回溯到上一节点
        }
    }
}

分析：

• Constraint(t):约束函数，剪枝条件（剪去不可行解）
• Bound(t):限界函数，剪枝条件（剪去不可能最优的解）
• Solution(t)：判断在当前扩展节点处是否已得到问题的可行解。它返回值为true时，当前扩展节点处x[1：t]是问题的可行解。此时，由Output(x)记录或输出得到的可行解。它的返回值为false时，在当前扩展结点处x[1:t]只是问题的部分解，还需向纵深方向继续搜索。
• 搜索边界： f(n,t)和g(n,t)

9、参考资料

• 算法设计与分析（第四版）