EGES:Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba
阿里的EGES是Graph Embedding的一个经典应用,在内容冷启和物料召回上面有较多的落地潜力。主要思想是根据用户交互的物料作为节点构建物料图,在传统的DeepWalk学习节点Embedding的基础上,使用attention融合节点的side information,使得学习到的物料Embedding包含更丰富、精准的信息。
动机
为了解决淘宝推荐的三大挑战:
- Scalability 扩展性,淘宝有十亿量级的用户和二十亿量级的物料
- Sparsity 稀疏性,很多用户有交互的物料非常少,用户或者物料很难学习的充分
- Cold Start 冷启动问题,每小时有上百万的新物料上线,新物料的推荐是个很大的问题
优化目标
给定图 G = ( V , E ) G = (V, E) G=(V,E), V V V表示节点集合, E E E表示边集合,目标是学习一个映射函数 Φ : V → R d \Phi : V \rightarrow R^d Φ:V→Rd,使得每个节点 v ∈ V v \in V v∈V映射成一个 d d d维向量。
使用DeepWalk方式学习Graph Embedding,DeepWalk使用Word2vec来学习图的节点表示。应用Skip-gram来优化,表示如下。
min
Φ
=
∑
v
∑
c
∈
N
(
v
)
P
r
(
c
∣
Φ
(
v
)
)
\min_{\Phi} = \sum_v \sum_{c \in N(v)} Pr(c \vert \Phi(v))
Φmin=v∑c∈N(v)∑Pr(c∣Φ(v))
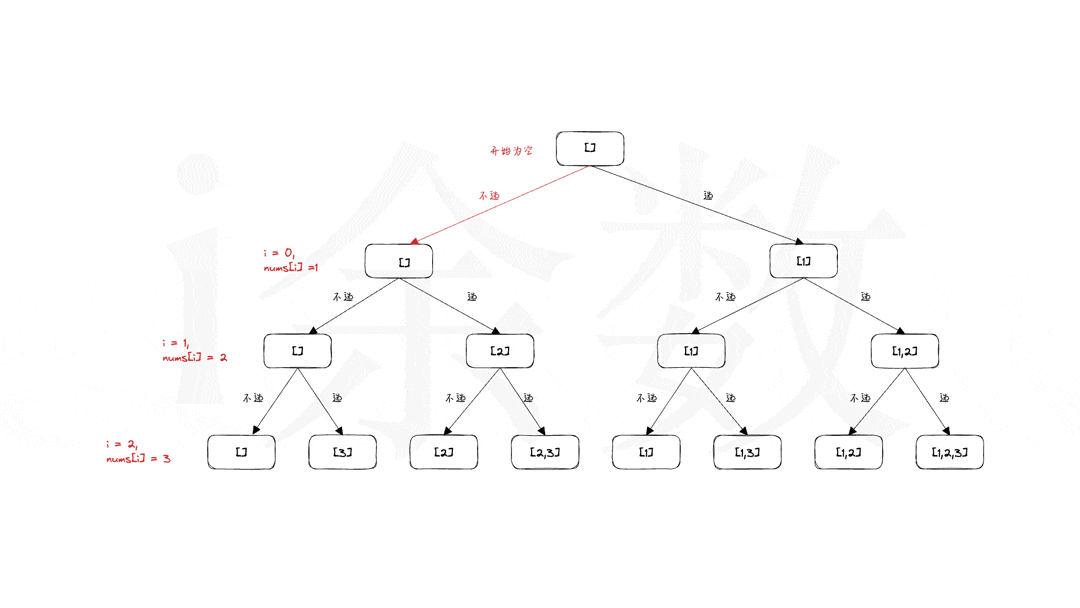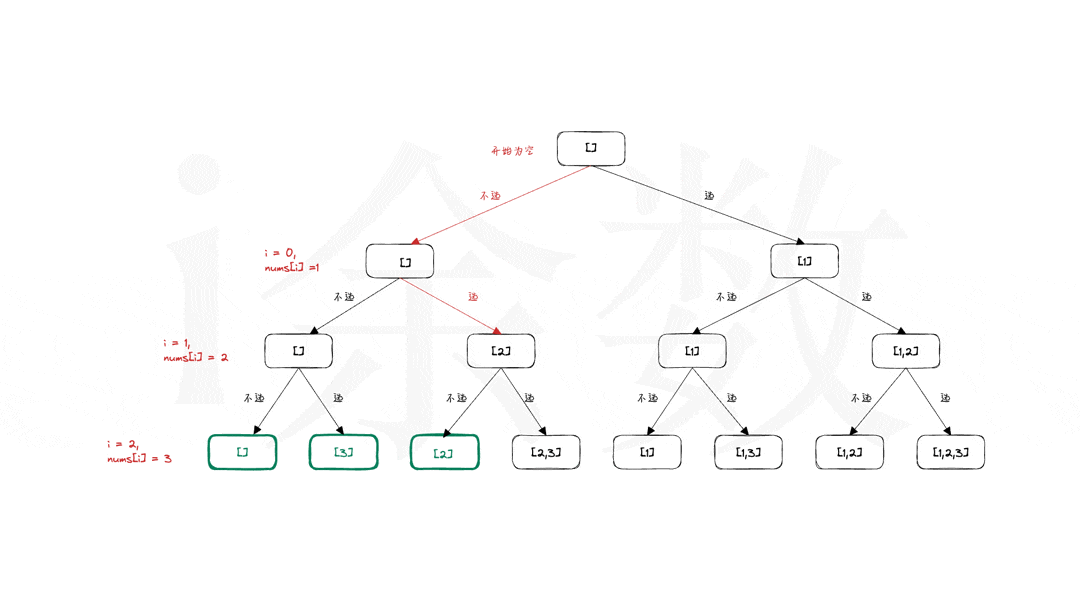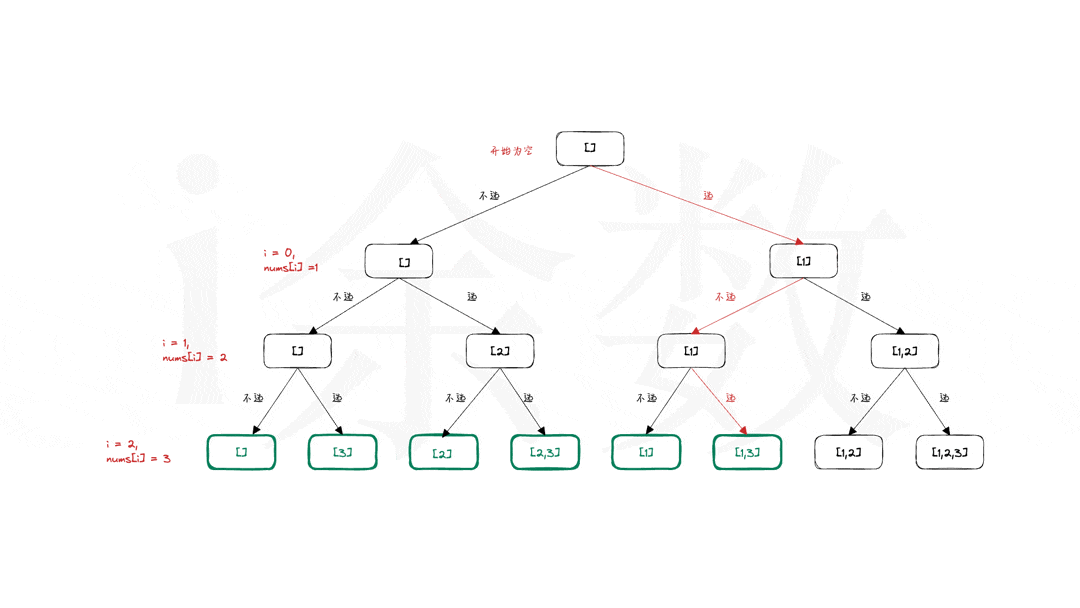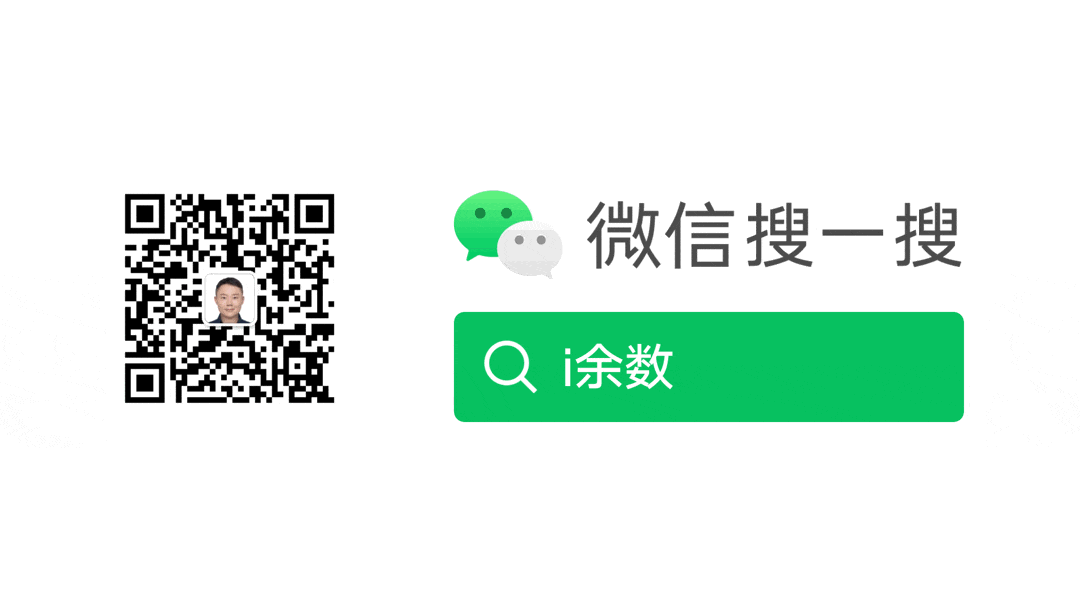
构建图
构建有向图,采样节点序列。需要做清洗:点击后停留不超过1s的行为去掉;3个月内购买超过1000个物料或者超过3500个点击的用户去掉;对于物料ID不变但是内容有更新的物料去掉。
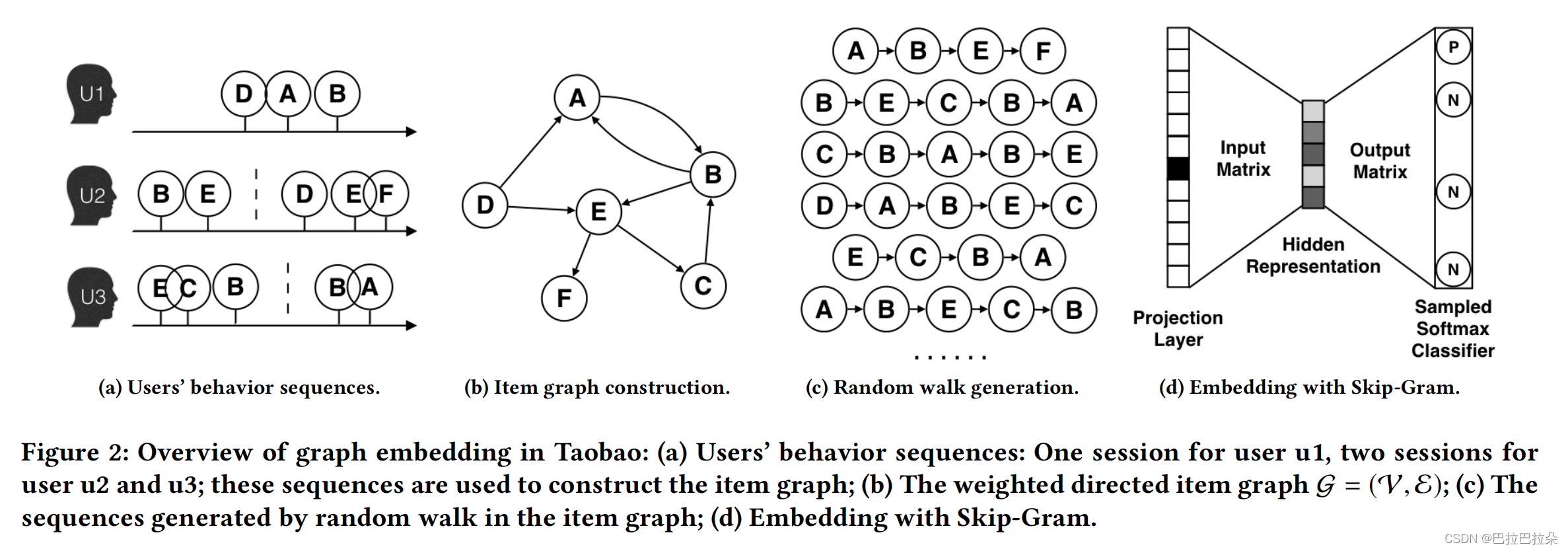
随机游走的节点转移概率定义如下,
M
M
M表示节点的邻接矩阵,
M
i
j
M_{ij}
Mij表示节点
i
i
i到节点
j
j
j的权重,节点的权重定位为相邻节点
i
i
i跳转到节点
j
j
j的频率。
P
(
v
j
∣
v
i
)
=
{
M
i
j
∑
j
∈
N
+
(
v
i
)
M
i
j
v
j
∈
N
+
(
v
i
)
0
e
i
j
∉
E
P(v_j|v_i)= \begin{cases} \frac {M_{ij}} {\sum_{j \in N_+(v_i) M_{ij}}} & \text v_j \in N_+(v_i)\\ 0& \text e_{ij} \notin E \end{cases}
P(vj∣vi)={∑j∈N+(vi)MijMij0vj∈N+(vi)eij∈/E
然后应用优化目标
min
Φ
=
−
log
P
r
(
(
v
i
−
w
,
.
.
.
,
v
i
+
w
)
\
v
i
∣
Φ
(
v
i
)
)
\min_{\Phi} = - \log Pr( (v_{i-w}, ..., v_{i+w} ) \backslash v_i \vert \Phi (v_i))
Φmin=−logPr((vi−w,...,vi+w)\vi∣Φ(vi))
其中
w
w
w是窗口大小,使用节点独立性假设
P
r
(
(
v
i
−
w
,
.
.
.
,
v
i
+
w
)
\
v
i
∣
Φ
(
v
i
)
)
=
∏
j
=
i
−
w
,
j
≠
i
i
+
w
P
r
(
v
j
∣
Φ
(
v
i
)
)
Pr( (v_{i-w}, ..., v_{i+w} ) \backslash v_i \vert \Phi (v_i)) = \prod_{j=i-w,j \neq i}^{i+w} Pr(v_j \vert \Phi (v_i))
Pr((vi−w,...,vi+w)\vi∣Φ(vi))=j=i−w,j=i∏i+wPr(vj∣Φ(vi))
基于负采样方法,
N
(
v
i
)
′
N(v_i)'
N(vi)′表示节点
v
i
v_i
vi的负采样,可以得到优化目标的详细形式
min
Φ
=
log
σ
(
Φ
(
v
i
)
T
Φ
(
v
j
)
)
+
∑
t
∈
N
(
v
i
)
′
log
σ
(
−
Φ
(
v
t
)
Φ
(
v
i
)
)
\min_{\Phi} = \log \sigma (\Phi(v_i)^T \Phi(v_j) ) + \sum_{t \in N(v_i)'} \log \sigma (- \Phi(v_t) \Phi(v_i))
Φmin=logσ(Φ(vi)TΦ(vj))+t∈N(vi)′∑logσ(−Φ(vt)Φ(vi))
GES:Graph Embedding with Side Information
除了物料ID之外,还可以加入其他的物料信息,比如物料一级类目、二级类目、所属商家、所属店铺等信息,
W
W
W表示物料ID的Embedding矩阵,其中
W
v
0
W_v^0
Wv0表示物料节点
v
v
v的ID的Embedding,
W
v
s
W_v^s
Wvs表示第
s
s
s个sideinfo,
H
v
H_v
Hv表示融合之后的Embedding
H
v
=
1
n
+
1
∑
s
=
0
n
W
v
s
H_v = \frac {1} {n+1} \sum_{s = 0}^n W_v^s
Hv=n+11s=0∑nWvs
EGES:Enhanced Graph Embedding with Side Information
上面各个sideinfo融合的时候权重是一样的,实际情况肯定是不同的sideinfo权重不一样,设置不同的权重更符合事实。设置一个权重矩阵
A
∈
R
∣
V
∣
×
(
n
+
1
)
A \in R^{|V| \times (n+1)}
A∈R∣V∣×(n+1) 表示各个节点在各个sideinfo上面的权重,融合后的Embedding为
H
v
=
∑
j
=
0
n
e
a
v
j
W
v
j
∑
j
=
0
n
e
a
v
j
H_v = \frac {\sum_{j=0}^n e^{a_v^j} W_v^j } { \sum_{j=0}^n e^{a_v^j} }
Hv=∑j=0neavj∑j=0neavjWvj
学习算法
节点 v v v的Embedding是 H v H_v Hv,节点 v v v的一个邻居节点的Embedding表示为 Z u ∈ R d Z_u \in R^d Zu∈Rd,label为 y y y,那么代入上面的优化目标,可以得到
L
(
v
,
u
,
y
)
=
−
[
y
log
(
σ
(
H
v
T
Z
u
)
)
+
(
1
−
y
)
log
(
1
−
σ
(
H
v
T
Z
u
)
)
]
L(v,u,y) = - [ y \log (\sigma (H_v^TZ_u)) + (1-y) \log (1 - \sigma(H_v^TZ_u) ) ]
L(v,u,y)=−[ylog(σ(HvTZu))+(1−y)log(1−σ(HvTZu))]
梯度求解如下

算法步骤


实验结果
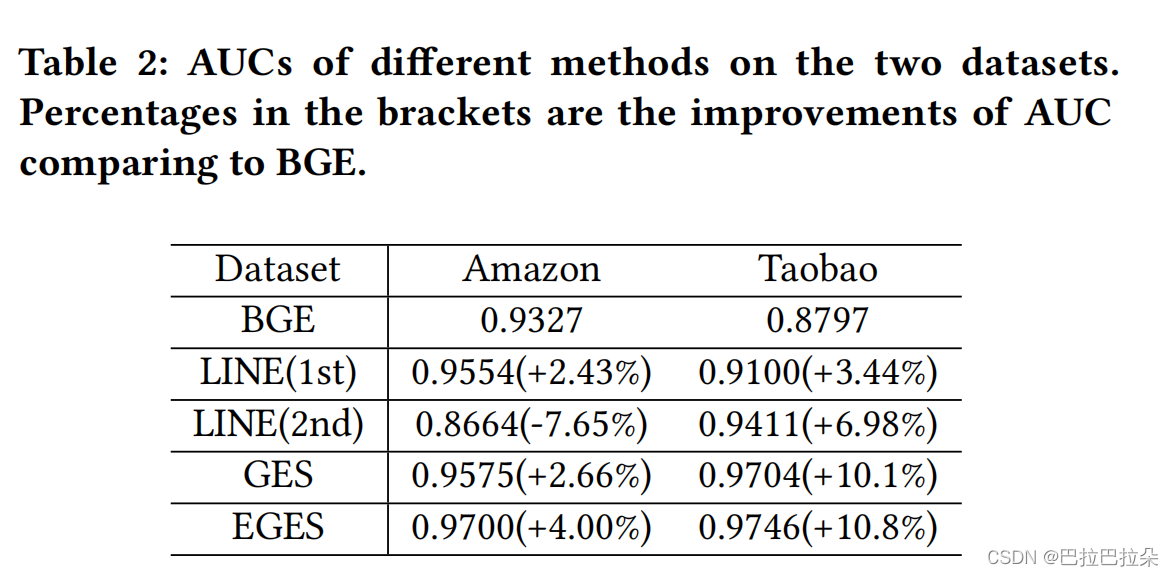
DeepWalk相关
EGES使用了DeepWalk作为Graph节点Embedding的学习,这里简要回顾下DeepWalk。
DeepWalk优缺点:
优点:
首个将自然语言处理和深度学习应用到图机器学习中
稀疏数据场景性能很好
缺点:
随机均匀游走
需要大量随机游走序列
学到的是局部信息,很难学到全局信息
仅利用到节点的连接信息,没有利用节点的属性
使用的是word2vec,网络层级不深
DeepWalk的主要思想是将图中节点进行采样得到一系列节点序列,将这些节点序列看做句子,节点看做词汇,套用自然语言处理处理领域的word2vec对节点进行无监督编码处理,得到节点Embedding。使得在图结构中比较接近的节点的Embedding在向量空间中也比较接近。
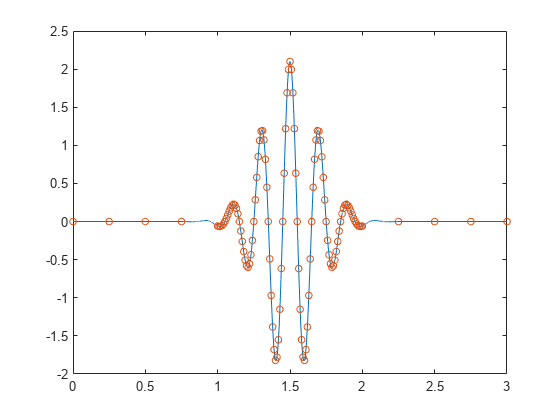
如下图所示,图中比较接近的点编码后的Embedding(二维,d=2)在向量空间上也是比较接近。
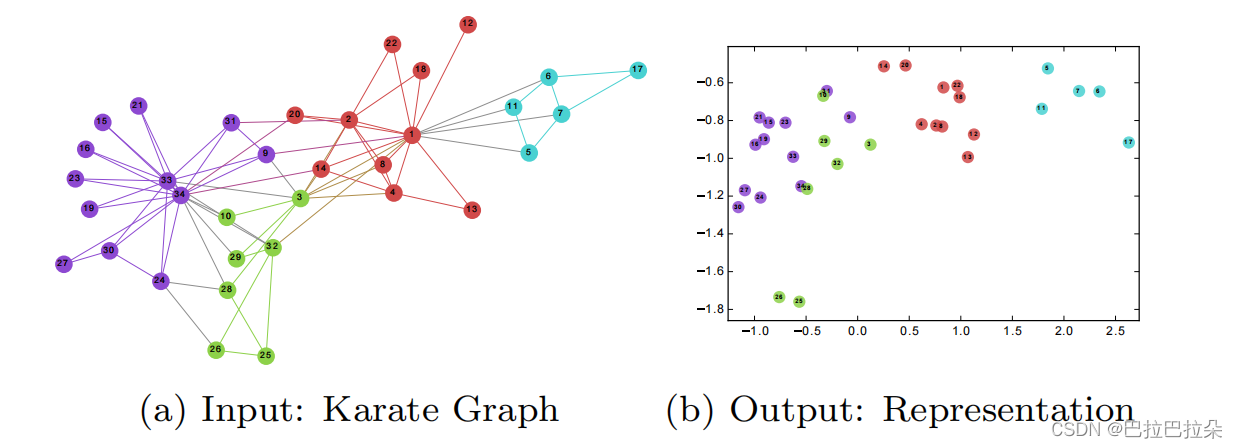
为什么可以套用Word2vec
因为自然语言处理中,句子中的词汇的分布是幂律分布,少量的词大量使用,有大量的长尾词汇。而一个现实的图中,也是少量的节点有大量的连接(度),大部分节点的度比较少,二八定律也非常明显,因此随机采样的节点序列也是符合幂律分布的,因此可以套用。

使用skip-gram算法,用中心词预测周围词,
w
w
w表示窗口大小
min
Φ
=
−
log
P
r
(
(
v
i
−
w
,
.
.
.
,
v
i
+
w
)
\
v
i
∣
Φ
(
v
i
)
)
\min_{\Phi} = - \log Pr( (v_{i-w}, ..., v_{i+w} ) \backslash v_i \vert \Phi (v_i))
Φmin=−logPr((vi−w,...,vi+w)\vi∣Φ(vi))
DeepWalk算法步骤
设定好窗口大小
w
w
w,Embedding大小
d
d
d,每个节点随机游走的次数
γ
\gamma
γ,游走的序列长度
t
t
t


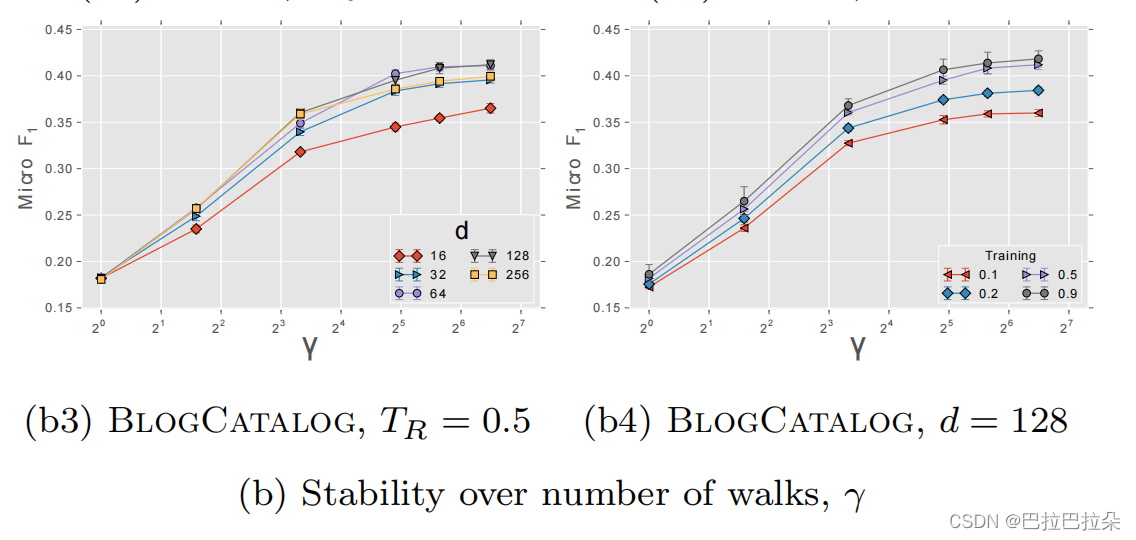
实验结果
因为是无监督产生的Embedding结果,实验评估的时候讲这些Embedding作为中间结果来做多分类,计算F1值,可以看到标注的label比例越大,DeepWalk效果越好。
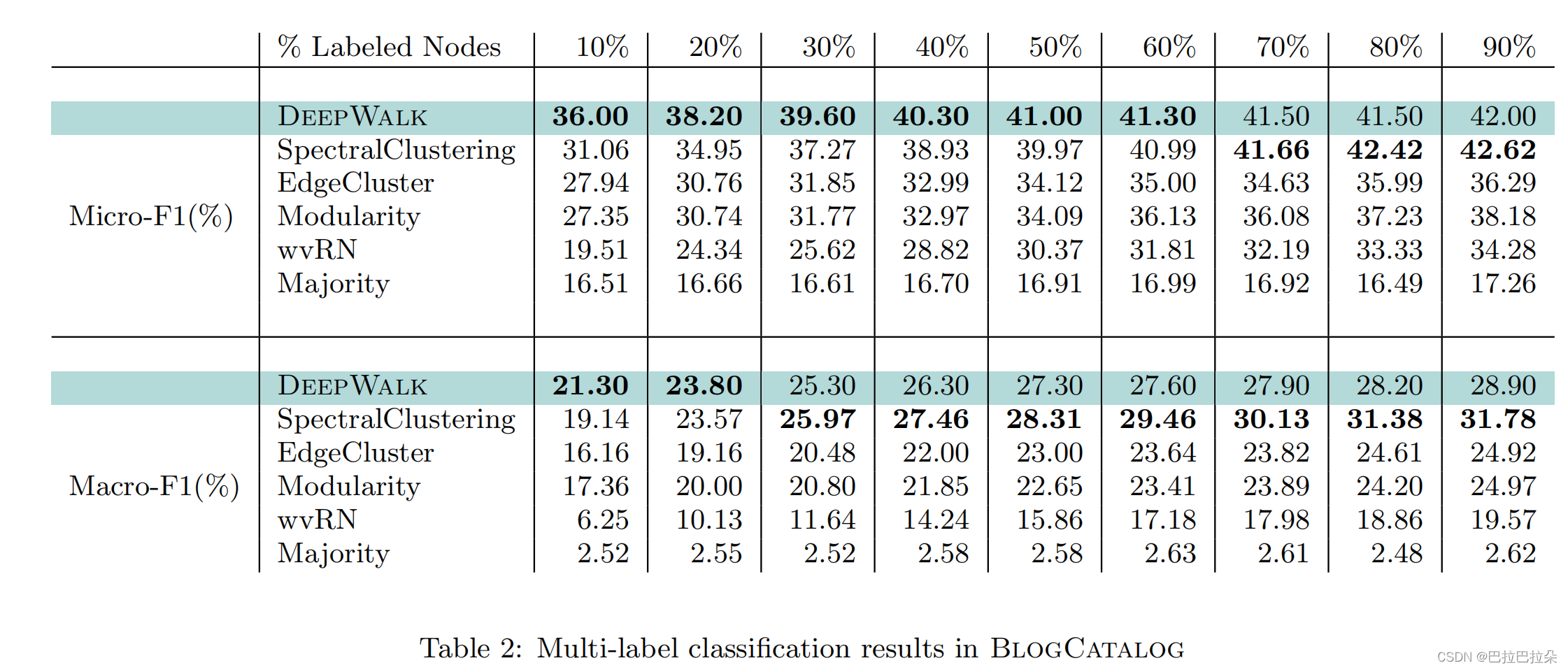

节点的游走次数
γ
\gamma
γ对效果的影响,大概在
γ
>
10
\gamma > 10
γ>10之后效果增长缓慢。