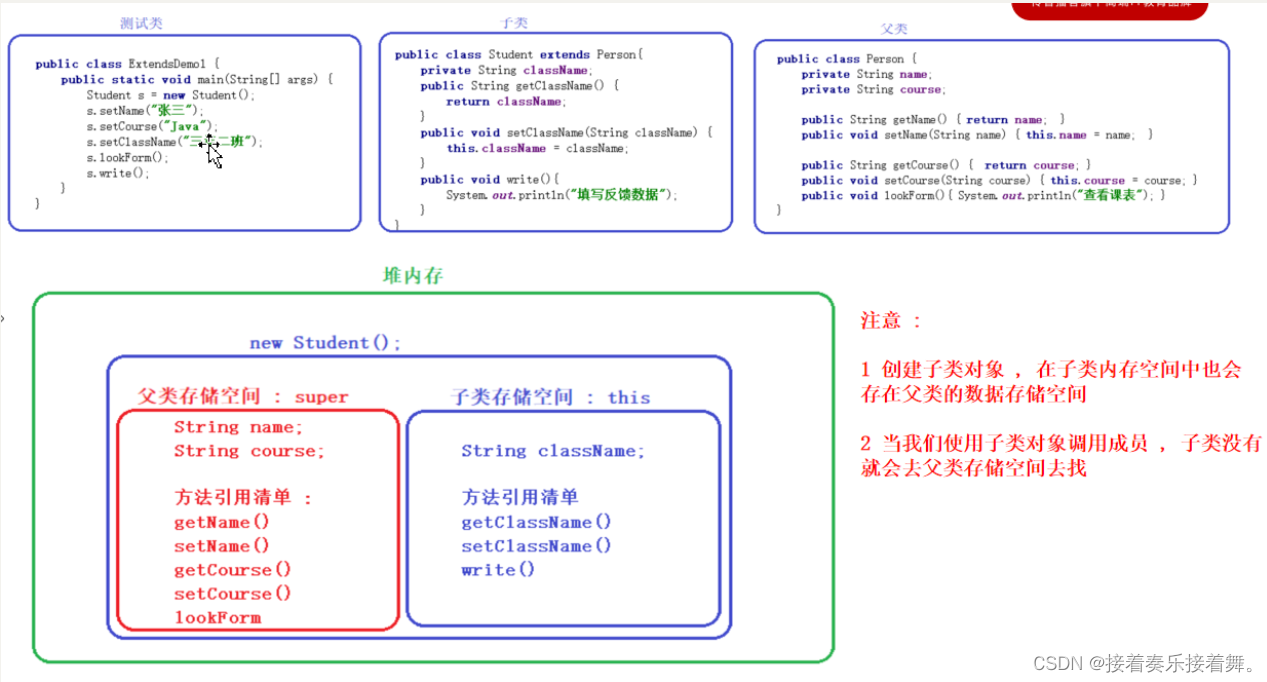
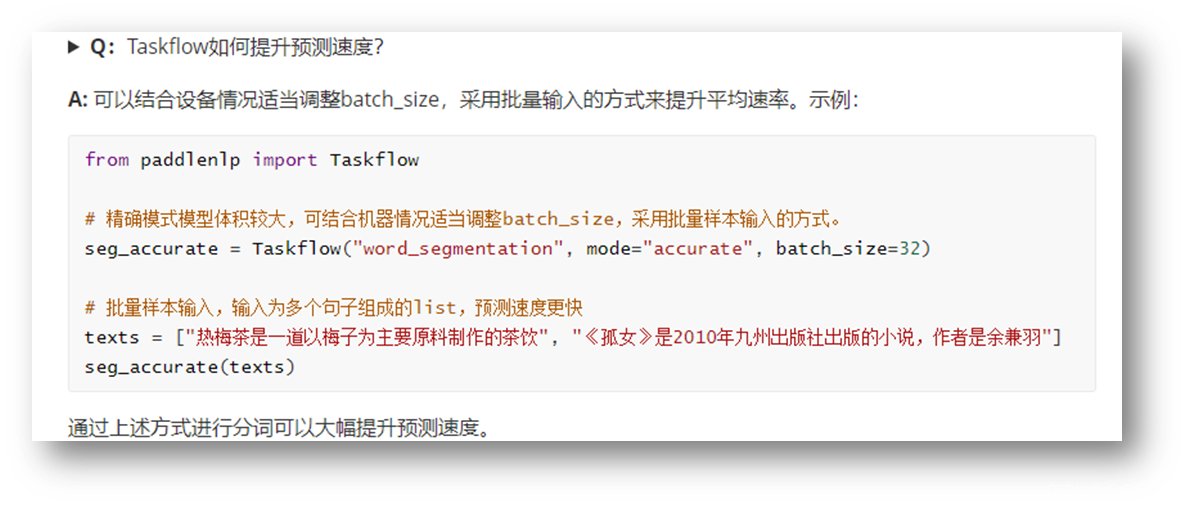
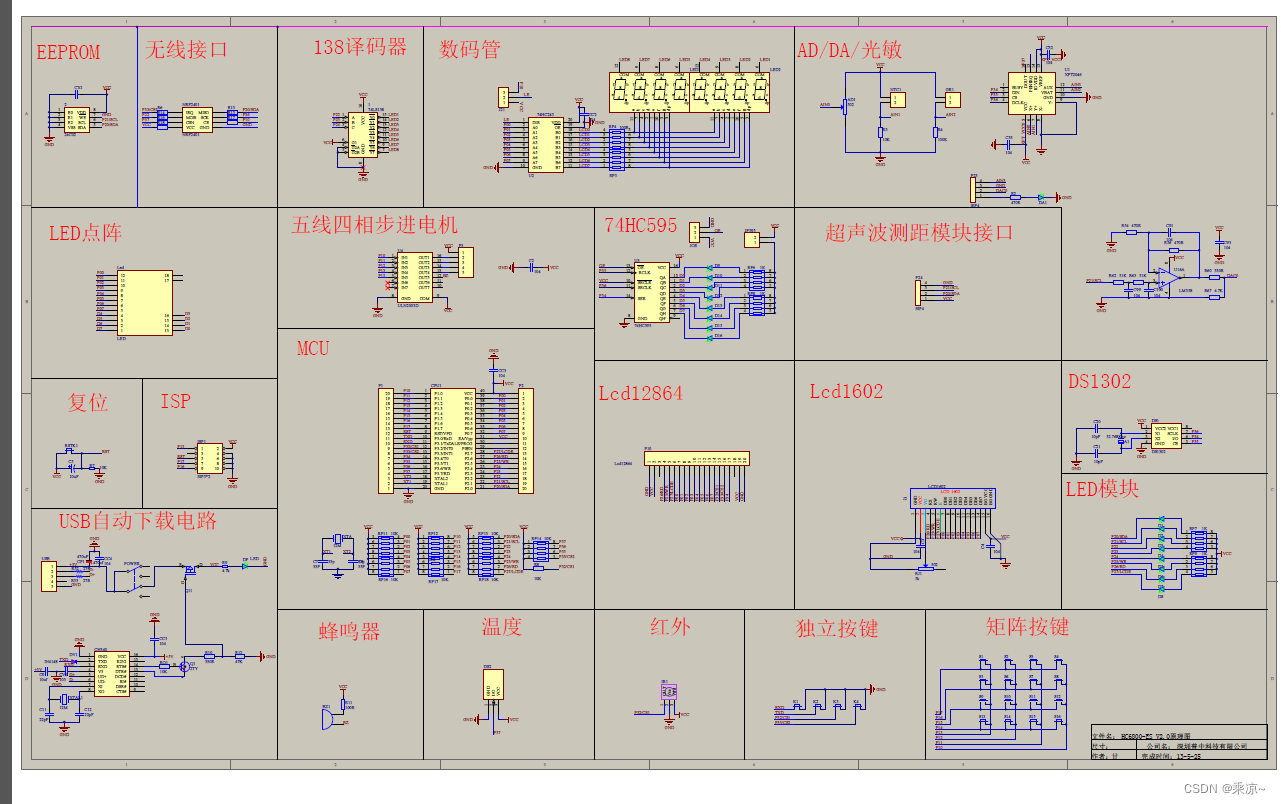
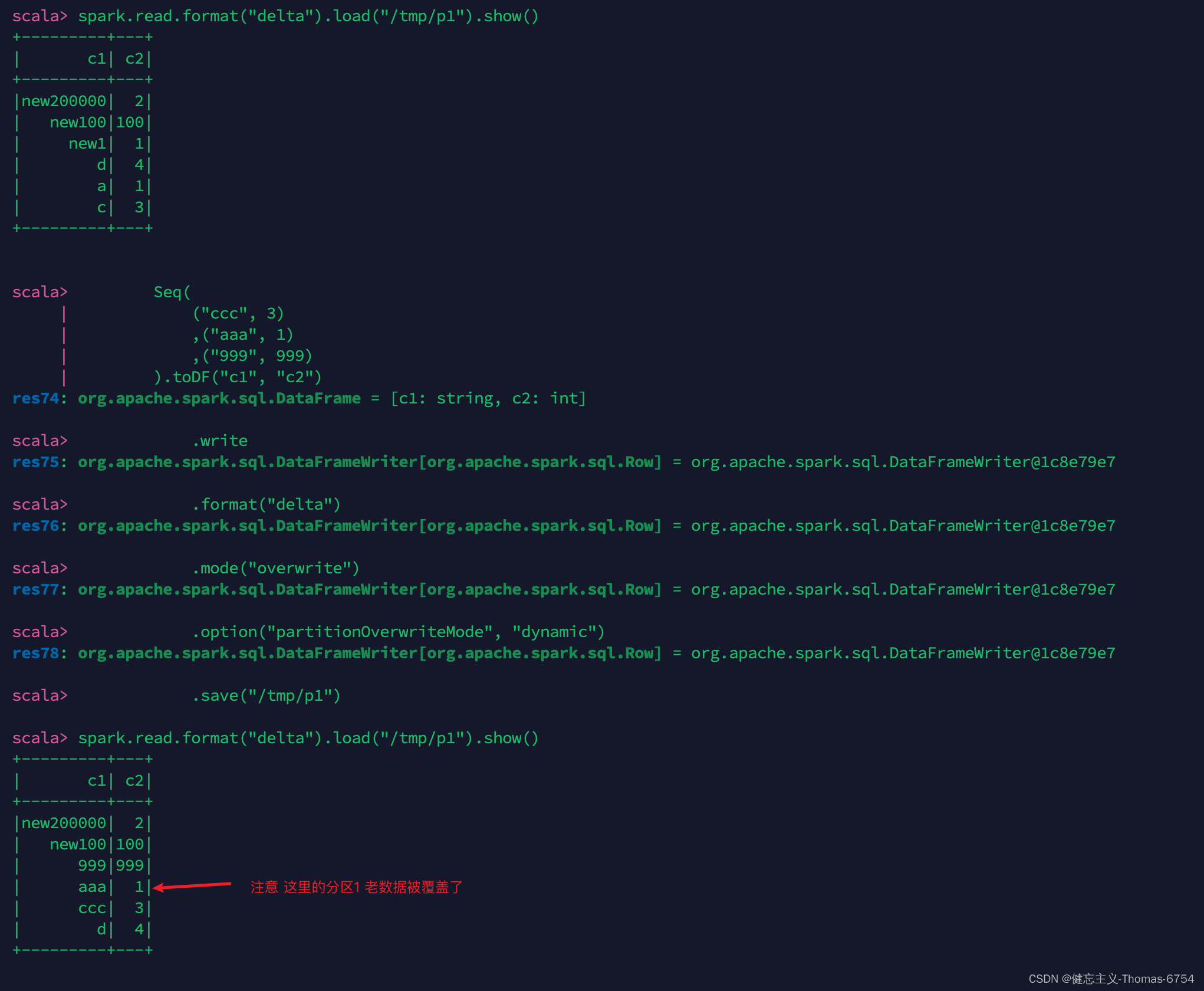
堆宝塔游戏是让小朋友根据抓到的彩虹圈的直径大小，按照从大到小的顺序堆起宝塔。但彩虹圈不一定是按照直径的大小顺序抓到的。聪明宝宝采取的策略如下：

• 首先准备两根柱子，一根 A 柱串宝塔，一根 B 柱用于临时叠放。
• 把第 1 块彩虹圈作为第 1 座宝塔的基座，在 A 柱放好。
• 将抓到的下一块彩虹圈 C 跟当前 A 柱宝塔最上面的彩虹圈比一下，如果比最上面的小，就直接放上去；否则把 C 跟 B 柱最上面的彩虹圈比一下：
• • 如果 B 柱是空的、或者 C 大，就在 B 柱上放好；
• • 否则把 A 柱上串好的宝塔取下来作为一件成品；然后把 B 柱上所有比 C 大的彩虹圈逐一取下放到 A 柱上，最后把 C 也放到 A 柱上。

重复此步骤，直到所有的彩虹圈都被抓完。最后 A 柱上剩下的宝塔作为一件成品，B 柱上剩下的彩虹圈被逐一取下，堆成另一座宝塔。问：宝宝一共堆出了几个宝塔？最高的宝塔有多少层？

输入格式：

输入第一行给出一个正整数 N（≤103），为彩虹圈的个数。第二行按照宝宝抓取的顺序给出 N 个不超过 100 的正整数，对应每个彩虹圈的直径。

输出格式：

在一行中输出宝宝堆出的宝塔个数，和最高的宝塔的层数。数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：

11
10 8 9 5 12 11 4 3 1 9 15

输出样例：

4 5

样例解释：

宝宝堆成的宝塔顺次为：

• 10、8、5
• 12、11、4、3、1
• 9
• 15、9

#include<bits/stdc++.h>
using namespace std;
stack<int>A, B;
queue<int>Q;
int N, M, K, ans,sum;

int main()
{
    cin >> N;
    while (N--)
    {
        cin >> M;
        Q.emplace(M);
    }
    while (!Q.empty())
    {
        K = Q.front();
        if (A.empty() || K < A.top())
            A.push(K);
        else
        {
            if (B.empty() || K > B.top())
                B.push(K);
            else
            {
                sum++;
                int a = A.size();
                ans = max(ans, a);
                stack<int>s;
                A = s;
                while (!B.empty() && B.top() > K)
                {
                    A.push(B.top());
                    B.pop();
                }
                A.push(K);
            }
        }
        Q.pop();
    }
    if (!A.empty())
    {
        int a = A.size();
        ans = max(a, ans);
        sum++;
    }
    if (!B.empty())
    {
        int b = B.size();
        ans = max(ans, b);
        sum++;
    }
    cout <<  sum << " " << ans << endl;
    return 0;
}