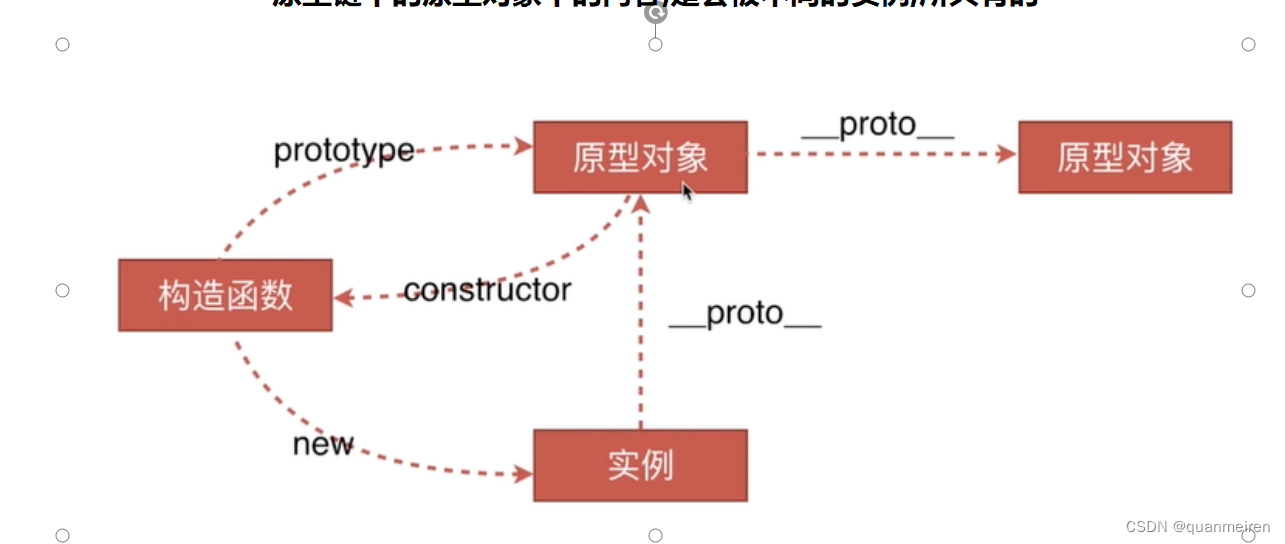
对于同一个竖直向上量子比特,不对他进行任何的干扰,进行第一次水平测试实验会随机得到一个一或者负一,之后再进行多少次水平测试实验都与第一次的试验结果是相同的。
我们换用其他的竖直向上量子比特,或者对原来的量子比特进行干扰,对原来那个竖直向上的量子比特进行干扰,当然还是要最后还是要保证它是竖直向上的,再进行水平测试实验,这一次,我们不一定会得到和上一段当中的一样的实验结果,也就是说,当量子比特被干扰或者是被更换之后的实验和前一次实验是独立的。但是当第一次实验完成之后,如果不对量子比特做任何的干扰,那么,实验结果将和第一次永远保持相同。(观察的方向变了,这种观察就变成了干扰)

bra:左矢,指复数向量|b>的共轭向量<b|
ket:右矢,指复数向量|a>本身

狄拉克符号:<b|a>
狄拉克符号代表两个复数向量进行内积。


内积为0,叫做正交:

狄拉克符号允许结合律

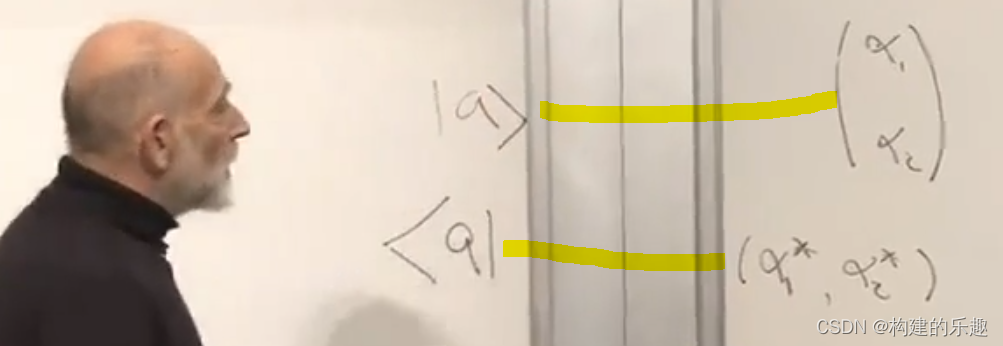
向量(上)和他的共轭向量(下)
在一次具体测自旋实验中,只会得到+1 -1结果,不会得到+1 -1在轴上的分量。但是,多次测量量子的自旋的平均值,量子的自旋就会和经典向量表现相似,这个时候平均值是分量。

小实验:
对于粒子的自旋方向,我们有AB两个命题,考察A
∨
\vee
∨B,该粒子事先已经被制备为自旋向z轴的正向:
A:粒子自旋方向指向z轴的正向。
B:粒子自旋方向指向x轴的正向。
做两次独立的实验:
第一次,
我们先验证B,也就是沿着x轴正向观察,此时,根据上面所讲的粒子实验结果具有的量子特性(只会得到+1,-1,多次实验的平均值应为0,但是我们只验证一次。),我们会有50%的概率观察到+10, 50%的概率观察到-1。
在这次观察后,粒子的自旋方向被我们的观察干扰,变成了沿x轴正向,或是沿x轴负向,这太恐怖了!
随后,我们验证A, 也就是沿着z轴的正向观察,此时,根据上面所讲的粒子实验结果具有的量子特性(只会得到+1,-1,多次实验的平均值应为0,但是我们只验证一次。),我们竟然会有50%的概率观察到-1。
总结起来,A
∨
\vee
∨B这个命题在这个观察次序下,竟然不一定是正确的,会有25%的概率为假。
第二次,
我们先验证A,再验证B,这一次非常幸运,由于该粒子事先已经被制备为自旋向z轴的正向,我们第一次观察A一定会得到一个z轴的正向的结果,那么,A
∨
\vee
∨B这个命题一定是真的。
按照经典理论,A ∨ \vee ∨B一定是真的,不管按什么次序观察,因为经典理论中,观察不会干扰实验。
复数向量空间的性质:

最重要的那条,内积的顺序交换,结果不再相等,而是互为复共轭。