机器学习——损失函数（lossfunction）

news2024/11/23 16:48:53

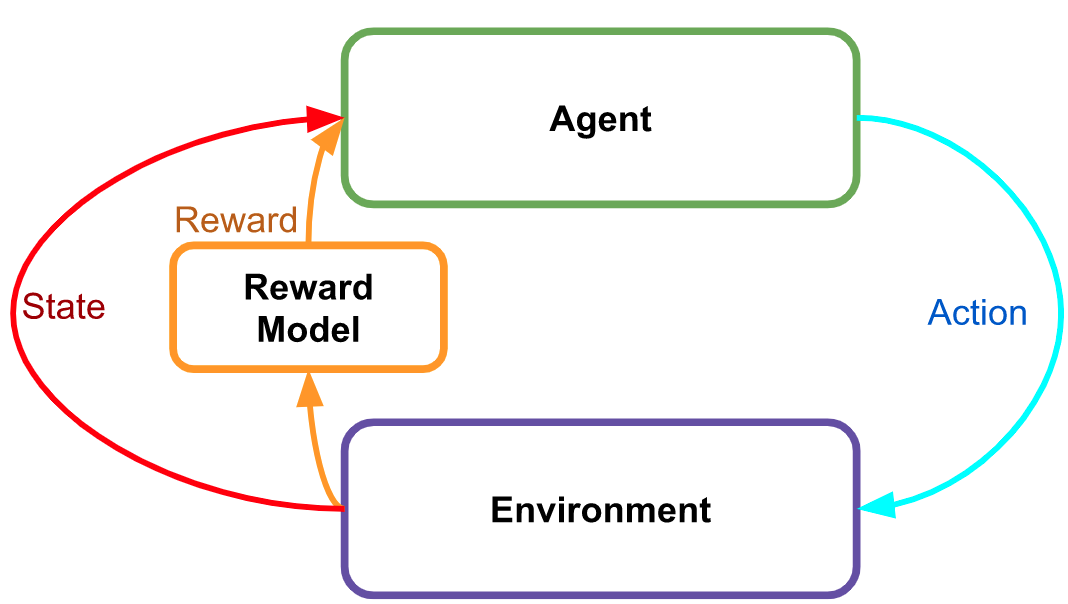
问：非监督式机器学习算法使用样本集中的标签构建损失函数。

答：错误。非监督式机器学习算法不使用样本集中的标签构建损失函数。这是因为非监督式学习算法的目的是在没有标签的情况下发现数据集中的特定结构和模式，因此它们依赖于不同于监督式学习的算法。因此，它们不会使用标签来训练模型。相反，它们使用不同的技术，例如聚类，降维和异常检测来发现数据中的模式和结构。

一、非监督式学习

非监督学习的训练样本没有已知标签，常需要通过非监督学习去发现样本间的结构关系。
非监督学习这块内容由两部分组成：K邻近法和主成分分析。

K-means

聚类是最常见的非监督学习应用。K-means是最常见的聚类学习算法。
K-means算法的输入包括：训练集样本，和需要划分的类别K。

二、什么是损失函数：

简单的理解就是每一个样本经过模型后会得到一个预测值，然后得到的预测值和真实值的差值就成为损失（当然损失值越小证明模型越是成功），我们知道有许多不同种类的损失函数，这些函数本质上就是计算预测值和真实值的差距的一类型函数，然后经过库（如pytorch，tensorflow等）的封装形成了有具体名字的函数。

三、为什么需要损失函数：

我们上文说到损失函数是计算预测值和真实值的一类函数，而在机器学习中，我们想让预测值无限接近于真实值，所以需要将差值降到最低（在这个过程中就需要引入损失函数）。而在此过程中损失函数的选择是十分关键的，在具体的项目中，有些损失函数计算的差值梯度下降的快，而有些下降的慢，所以选择合适的损失函数也是十分关键的。

四、损失函数通常使用的位置：

在机器学习中，我们知道输入的feature（或称为x）需要通过模型（model）预测出y，此过程称为向前传播（forward pass），而要将预测与真实值的差值减小需要更新模型中的参数，这个过程称为向后传播（backward pass），其中我们损失函数（lossfunction）就基于这两种传播之间，起到一种有点像承上启下的作用，承上指：接収模型的预测值，启下指：计算预测值和真实值的差值，为下面反向传播提供输入数据。

五、监督学习及其目标函数：

损失函数（loss function）是用来估量你模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。

损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。

模型的结构风险函数包括了经验风险项和正则项，通常可以表示成如下式子（一般来说，监督学习可以看做最小化下面的目标函数）：

式子左边表示经验风险函数，损失函数是其核心部分；式子右边是正则项。式子整体是结构风险函数，其由经验风险函数和正则项组成。

其中，第一项L(yi,f(xi;w)) 衡量我们的模型（分类或者回归）对第i个样本的预测值f(xi;w)和真实的标签yi之前的误差。因为我们的模型是要拟合我们的训练样本的，所以我们要求这一项最小。即前面的均值函数表示的是经验风险函数，L代表的是损失函数；

但正如上面说言，我们不仅要保证训练误差最小，我们更希望我们的模型测试误差小，所以我们需要加上第二项，也就是对参数w的规则化函数Ω(w)去约束我们的模型尽量的简单。即后面的Φ是正则化项（regularizer）或者叫惩罚项（penalty term），它可以是L1，也可以是L2，或者其他的正则函数。

整个式子表示的意思是找到使目标函数最小时的θ值。机器学习的大部分带参模型都和这个不但形似，而且神似，其实大部分无非就是变换这两项而已。

损失函数/loss函数

对于第一项Loss函数，如果是Square loss，那就是最小二乘；如果是Hinge Loss，那就是著名的SVM；如果是exp-Loss，那就是 Boosting；如果是log-Loss，那就是Logistic Regression；还有等等。不同的loss函数，具有不同的拟合特性，这个也得就具体问题具体分析的。

loss函数一般都是通过mle推导出来的。使用最大似然来导出代价函数的方法的一个优势是，它减轻了为每个模型设计代价函数的负担。明确一个模型p(y | x)则自动地确定了一个代价函数log p(y | x)。[深度学习]

下面主要列出几种常见的损失函数：

平方损失
0-1损失
Log损失
Hinge损失
指数损失
感知损失

平方损失函数（最小二乘法, Ordinary Least Squares ）

最小二乘法是线性回归的一种，OLS将问题转化成了一个凸优化问题。在线性回归中，它假设样本和噪声都服从高斯分布（为什么假设成高斯分布呢？其实这里隐藏了一个小知识点，就是中心极限定理），最后通过极大似然估计MLE可以推导出最小二乘式子，即平方损失函数可以通过线性回归在假设样本是高斯分布的条件下推导得到。

最小二乘的基本原则是：最优拟合直线应该是使各点到回归直线的距离和最小的直线，即平方和最小。换言之，OLS是基于距离的，而这个距离就是我们用的最多的欧几里得距离。为什么它会选择使用欧式距离作为误差度量呢（即Mean squared error， MSE），主要有以下几个原因：

简单，计算方便；
欧氏距离是一种很好的相似性度量标准；
在不同的表示域变换后特征性质不变。

平方损失（Square loss）的标准形式

当样本个数为n时，此时的损失函数变为：
$L(Y, f(X)) = \sum _{i=1}^{n}(Y - f(X))^2$
Y-f(X)表示的是残差，整个式子表示的是残差的平方和，而我们的目的就是最小化这个目标函数值，也就是最小化残差的平方和（residual sum of squares，RSS）。