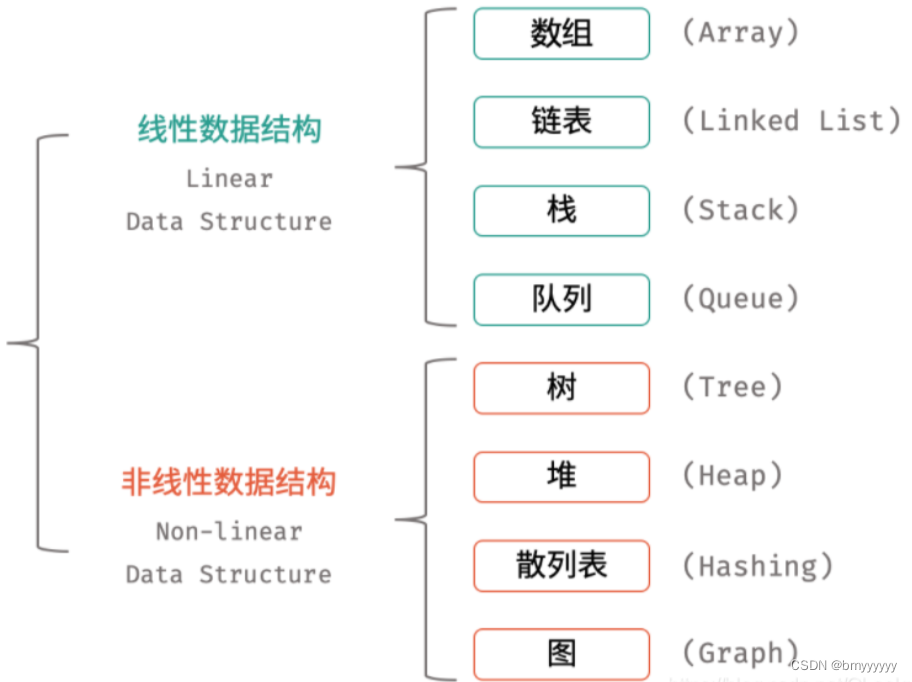
【计算机基本原理-数据结构】八大数据结构分类
- 1)数组
- 2)链表
- 3)队列
- 4)栈
- 5)树
- 6)图
- 7)堆
- 8)散列表(哈希表)
数据结构是计算机存储、组织数据的方式。一种好的数据结构可以带来更高的运行或者存储效率。数据在内存中是呈线性排列的,但是我们可以使用指针等道具,构造出类似“树形”的复杂结构。下面介绍八个常见的数据结构。如图所示:
1)数组
数组是可以再内存中连续存储多个元素的结构,在内存中的分配也是连续的。数组是一种线性结构,而且在物理内存中也占据着一块连续空间。数组中的元素通过数组下标进行访问,数组下标从 0 开始。例如下面这段代码就是将数组的第一个元素赋值为 1。
int[] data = new int[100];
data[0] = 1;
-
优点:
1、按照索引查询元素速度快
2、按照索引遍历数组方便
-
缺点:
1、数组的大小固定后就无法扩容了
2、数组只能存储一种类型的数据
3、添加,删除的操作慢,因为要移动其他的元素。
-
适用场景:
频繁查询,对存储空间要求不大,很少增加和删除的情况。
2)链表
链表是物理存储单元上非连续的、非顺序的存储结构,数据元素的逻辑顺序是通过链表的指针地址实现,每个元素包含两个结点,一个是存储元素的数据域(内存空间),另一个是指向下一个结点地址的指针域。

-
优点:
1、链表是很常用的一种数据结构,不需要初始化容量,可以任意加减元素。
2、添加或者删除元素时只需要改变前后两个元素结点的指针域指向地址即可,所以添加,删除很快。
-
缺点:
1、因为含有大量的指针域,占用空间较大。
2、查找元素需要遍历链表来查找,非常耗时。
-
适用场景:
数据量较小,需要频繁增加,删除操作的场景
数据访问:因为数据都是分散存储的,所以想要访问数据,只能从第一个数据开始,顺着指针的指向逐一往下访问。

数据添加:将Blue的指针指向的位置变成Green,然后再把Green的指针指向Yellow。

数据删除:只要改变指针的指向就可以了,比如删除Yellow,只需把Green指针指向的位置从Yellow编程Red即可。
虽然Yellow本身还存储在内存中,但是不管从哪里都无法访问这个数据,所以也就没有特意去删除它的必要了。今后需要用到Yellow所在的存储空间时,只要用新数据覆盖掉就可以了。

3)队列
队列与栈一样,也是一种线性表,不同的是,队列可以在一端添加元素,在另一端取出元素,也就是:先进先出。从一端放入元素的操作称为入队,取出元素为出队。

-
注意 :
栈是先进后出,队列是先进先出——两者虽然都是线性表,但原则是不同的,结构不一样嘛。
-
使用场景 :
因为队列先进先出的特点,在多线程阻塞队列管理中非常适用。
4)栈
栈是一种特殊的线性表,仅能在线性表的一端操作,栈顶允许操作,栈底不允许操作。
栈的特点是:先进后出,或者说是后进先出,从栈顶放入元素的操作叫入栈,取出元素叫出栈。
栈的结构就像一个集装箱,越先放进去的东西越晚才能拿出来,所以,栈常应用于实现递归功能方面的场景,例如斐波那契数列。

5)树
树是一种典型的非线性结构,它是由 n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做 “树” 是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
-
特点:
1、每个节点有零个或多个子节点。
2、没有父节点的节点称为根节点。
3、每一个非根节点有且只有一个父节点。
4、除了根节点外,每个子节点可以分为多个不相交的子树。
在日常的应用中,我们讨论和用的更多的是树的其中一种结构,就是二叉树。二叉树是树的特殊一种。
-
二叉树特点:
1、每个结点最多有两颗子结点。
2、左子树和右子树是有顺序的,次序不能颠倒。
3、即使某结点只有一个子树,也要区分左右子树。
二叉树是一种比较有用的折中方案,它添加,删除元素都很快,并且在查找方面也有很多的算法优化,所以,二叉树既有链表的好处,也有数组的好处,是两者的优化方案,在处理大批量的动态数据方面非常有用。
树有很多扩展的数据结构,包括平衡二叉树、红黑树、B+树等,这些数据结构二叉树的基础上衍生了很多的功能,在实际应用中广泛用到,例如 mysql 的数据库索引结构用的就是B+树,还有 HashMap 的底层源码中用到了红黑树。这些二叉树的功能强大,但算法上比较复杂,想学习的话还是需要花时间去深入的。
6)图
图是由结点的有穷集合V和边的集合E组成。其中,为了与树形结构加以区别,在图结构中常常将结点称为顶点,边是顶点的有序偶对,若两个顶点之间存在一条边,就表示这两个顶点具有相邻关系。按照顶点指向的方向可分为无向图和有向图:
- 有向图:

- 无向图:

7)堆
堆是一种图的树形结构,被用于实现“优先队列”(priority queues)。优先队列是一种数据结构,可以自由添加数据,但取出数据时要从最小值开始按顺序取出。在堆的树形结构中,各个顶点被称为“结点”(node),数据就存储在这些结点中。
-
堆的特点:
1、每个节点最多有两个子节点。
2、排列顺序必须从上到下,同一行从左到右。
3、堆中某个节点的值总是不大于或不小于其父节点的值。
4、存放数据时,一般会把新数据放在最下面一行靠左的位置。如果最下面一行没有多余空间时,就再往下另起一行,并把数据添加到这一行的最左端。
-
堆的性质:
1、堆是一个完全二叉树。
2、堆中某个结点的值总是不大于或不小于其父结点的值。
- 将根结点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
- 一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
- 一棵深度为k 且有2^k - 1个结点的二叉树称为满二叉树。也就是说除了叶子节点都有2个子节点,且所有的叶子节点都在同一层。

8)散列表(哈希表)
哈希表,也叫散列表,是根据关键码和值 (key和value) 直接进行访问的数据结构,通过key和value来映射到集合中的一个位置,这样就可以很快找到集合中的对应元素。例如,下列键(key)为人名,value为性别。
一般来说,我们可以把键当作数据的标识符,把值当作数据的内容。

-
具有以下的性质:
1、可以利用哈希函数快速访问到数组的目标数据。如果发生哈希冲突,就使用链表进行存储。
2、如果数组的空间太小,使用哈希表的时候就容易发生冲突,线性查找的使用频率也会更高;反过来,如果数组的空间太大,就会出现很多空箱子,造成内存的浪费。因此,给数组设定合适的空间非常重要。
3、在存储数据的过程中,如果发生冲突,可以利用链表在已有数据的后面插入新数据来解决冲突。这种方法被称为“链地址法”。除了链地址法以外,还有几种解决冲突的方法。其中,应用较为广泛的是“开放地址法”。

![[网络原理] 详解Cookie与Session](https://img-blog.csdnimg.cn/410357148cd74a068872b6481bf8fb4e.png)