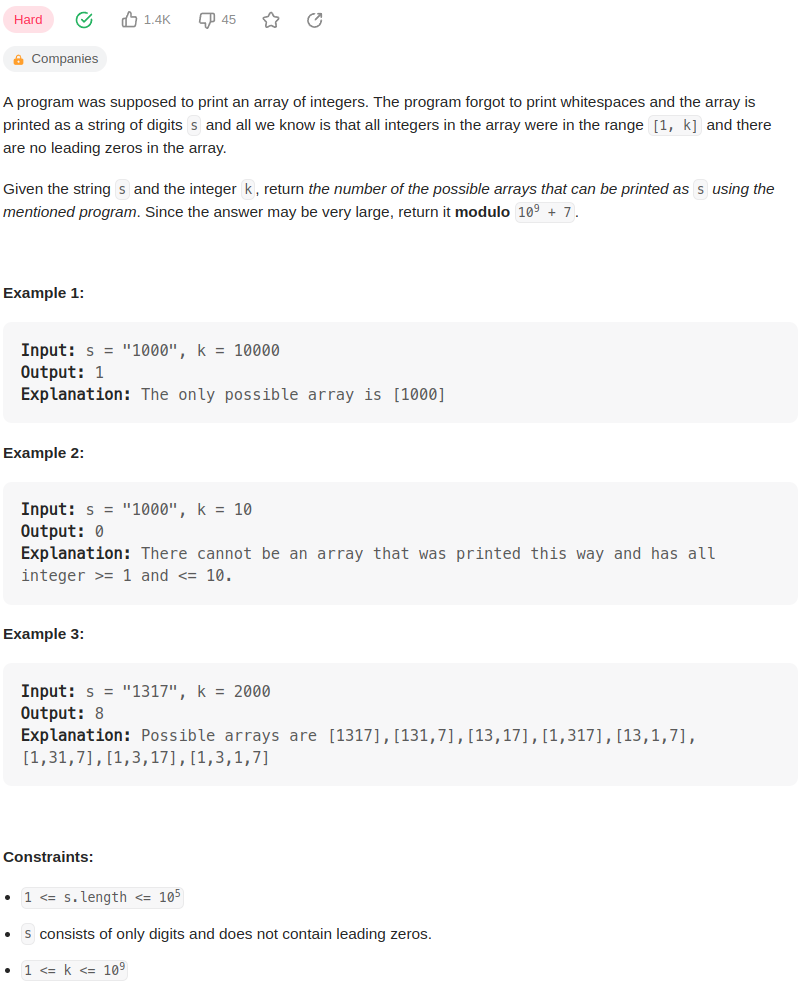
一台打印机没有把空格打印出来,以至于不知道打印出的 s 中到底有哪些数字。
现在知道数字的取值范围在1 ~ k, 数字开头不能是0.
返回可能的数字个数。取模109+7.
思路:
DP
假设dp[ i ]为 i ~ n位的s 所能组成的数字组合数。
从右到左遍历,说下为什么是从右到左。
因为数字要连续出现的,以“1317"为例,如果从左到右,比如现在遍历到 j = 2, 即第2个1,
而“131”这个数字中,如果取了“13”,那么和j=3的“7”组合时,就不连续了,变成了"13"和“7",这个是不好控制的。
下面以Example3的"1317"为例来说明。
初始状态,空字符串,个数为1,dp[4]=1,
i = 3, s[ i ] = “7”,7 < k, 7与空字符串组合,那么需要知道空字符串有多少种可能(dp[4] )。
这时dp[ 3 ] += dp [ 4 ].
i = 2, s[2] = “1”,1 < k,
“1”可与“7”组合成[1, 7],也可与空字符串组合成[1], 因此需要知道"7"有多少种可能( dp [ 3 ] ).
这时dp [ 2 ] += dp [ 3 ].
i = 1, s[ i ] = “3”, 3 < k, 可以选择"3"和“17”组合,那么需要知道“17”有多少种可能,
于是有[3, 17] 和 [3, 1, 7]
这时dp [ 1 ] += dp [ 2 ].
也可以选择“31“和”7“组合,31 < k, 那么需要知道"7"有多少种可能。
这时dp [ 1 ] += dp [ 3 ].
最后i = 0, s[0] = “1”, 1 < k, "1"可以和"317"组合,
dp[0] += dp[1]
13 < k , "13“和”17“组合,( [13, 17], [13, 1, 7], [13, 1] )
dp[0] += dp[2]
131 < k, "131"和“7”组合,( [131, 7] )
dp[0] += dp[3]
前提是当前数字 <= k, 如果当前数字 > k, 则进入下一个 i 的遍历。
如果当前s [ i ]为0,也进入下一遍历,因为数字不能是0开头。
最后返回dp[0], 即 0 ~ n-1的组合数。
public int numberOfArrays(String s, int k) {
final int MOD = (int)1e9+7;
int n = s.length();
int[] dp = new int[n+1]; //dp[i]:i~n的组合个数
char[] chs = s.toCharArray();
dp[n] = 1;
for(int i = n-1; i >= 0; i--) {
if(chs[i] == '0') continue; //0开头的不算
long sum = 0, num = 0;
for(int j = i; j < n; j++) {
num = num*10 + (chs[j]-'0');
if(num > k) break;
sum += dp[j+1];
}
dp[i] = (int)(sum % MOD);
}
return dp[0];
}

如果实在不好理解,可以参考下面的流程
初始状态,'': dp[4]=1
i=3,指向s[3]=7
j=3,指向s[3]=7
现在num=7
num (7) < k (2000)
[7 ~ 7] 和 [''] 组合
dp[3] += dp[4]=1
dp[3]=1
i=2,指向s[2]=1
j=2,指向s[2]=1
现在num=1
num (1) < k (2000)
[1 ~ 1] 和 [7~ 最后] 组合
dp[2] += dp[3]=1
j=3,指向s[3]=7
现在num=17
num (17) < k (2000)
[1 ~ 7] 和 [''] 组合
dp[2] += dp[4]=2
dp[2]=2
i=1,指向s[1]=3
j=1,指向s[1]=3
现在num=3
num (3) < k (2000)
[3 ~ 3] 和 [1~ 最后] 组合
dp[1] += dp[2]=2
j=2,指向s[2]=1
现在num=31
num (31) < k (2000)
[3 ~ 1] 和 [7~ 最后] 组合
dp[1] += dp[3]=3
j=3,指向s[3]=7
现在num=317
num (317) < k (2000)
[3 ~ 7] 和 [''] 组合
dp[1] += dp[4]=4
dp[1]=4
i=0,指向s[0]=1
j=0,指向s[0]=1
现在num=1
num (1) < k (2000)
[1 ~ 1] 和 [3~ 最后] 组合
dp[0] += dp[1]=4
j=1,指向s[1]=3
现在num=13
num (13) < k (2000)
[1 ~ 3] 和 [1~ 最后] 组合
dp[0] += dp[2]=6
j=2,指向s[2]=1
现在num=131
num (131) < k (2000)
[1 ~ 1] 和 [7~ 最后] 组合
dp[0] += dp[3]=7
j=3,指向s[3]=7
现在num=1317
num (1317) < k (2000)
[1 ~ 7] 和 [''] 组合
dp[0] += dp[4]=8
dp[0]=8