注意事项:
本题是"区间dp—石子合并"的扩展题,dp思路完全一样,就不多详细讲了,可以去那篇文章看,这题主要讲一下如何处理环形。
题目:
将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n 及每堆的石子数,并进行如下计算:
- 选择一种合并石子的方案,使得做 n−1 次合并得分总和最大。
- 选择一种合并石子的方案,使得做 n−1 次合并得分总和最小。
输入格式
第一行包含整数 n,表示共有 n 堆石子。
第二行包含 n 个整数,分别表示每堆石子的数量。
输出格式
输出共两行:
第一行为合并得分总和最小值,
第二行为合并得分总和最大值。
数据范围
1≤n≤200
输入:
4
1 3 5 2
输出:
22
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 410, INF = 0x3f3f3f; //N开两倍
int n, m, s[N], w[N]; //s存储前缀和,w存储原始值
int f[N][N], g[N][N]; //f存储max,g存储min
int main() {
cin >> n;
for (int i = 1; i<=n; i++) { //读入数组,并将数组复制一遍接到尾部,比如123,变为123123
cin >> m;
w[i] = w[i+n] = m;
}
//前缀和处理
for (int i = 1; i <= n*2; i++) s[i] = s[i-1] + w[i];
//dp(和基础版石子合并完全相同,只不过同时求了max和min)
memset(f, -INF, sizeof f); //f求max,所以初始为负无穷
memset(g, INF, sizeof g); //同理
for (int len = 1; len <= n; len++) { //枚举
for (int i = 1; i+len-1 <= (n*2); i++) {
int l = i, r = i+len-1;
if (len == 1) {
f[l][r] = g[l][r] = 0; continue;
}
for (int k = l; k < r; k++) {
f[l][r] = max(f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l-1]);
g[l][r] = min(g[l][r], g[l][k] + g[k+1][r] + s[r] - s[l-1]);
}
}
}
//再枚举所有断点的答案
int maxv = -INF, minv = INF;
for (int i = 1; i<=n; i++) {
maxv = max(maxv, f[i][i+n-1]);
minv = min(minv, g[i][i+n-1]);
}
cout << minv << endl << maxv << endl;
return 0;
}
思路:
处理环形其实非常简单,举个例子吧,比如我们当前的数组是1到8:
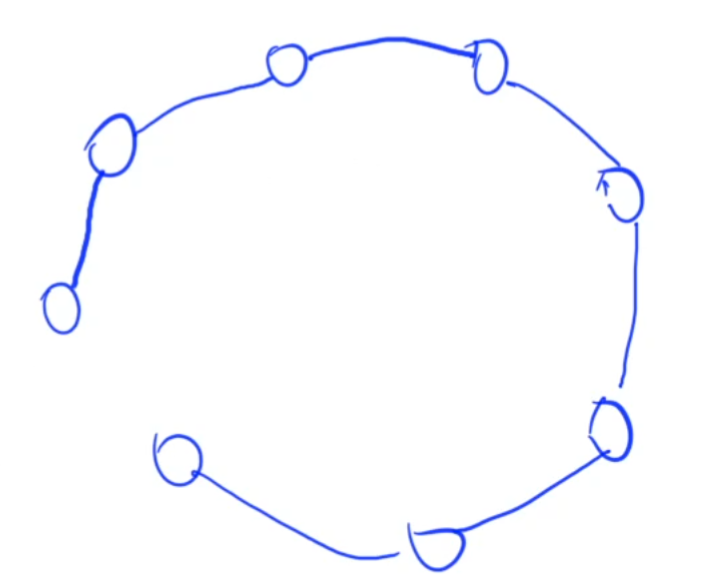
每条边代表一次合并,最终会有n-1次合并,并存在一个缺口,
同时可以发现,缺口所在的位置,就代表存在的一种合并方案,
那么枚举所有缺口,也就是计算出了所有的方案。
但按照常规枚举肯定是不行的,
因为本身石子合并就已经是n^3的时间复杂度了,
再枚举n个缺口,就是n^4,肯定会超时,那么就需要用到环形优化,
即,将链复制一份接在尾部,并对这个链进行dp即可:
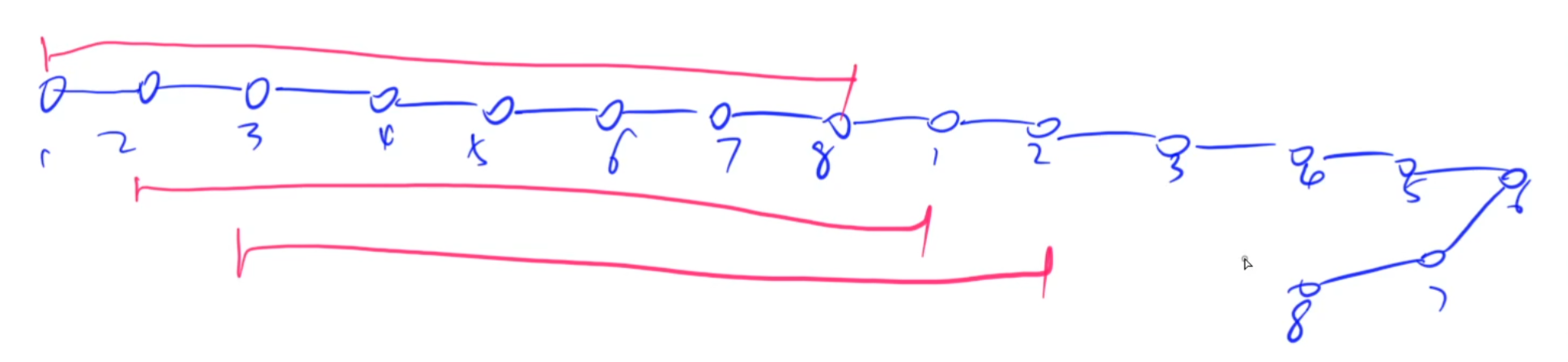
如果有所帮助请给个免费的赞吧~有人看才是支撑我写下去的动力!
声明:
算法思路来源为y总,详细请见https://www.acwing.com/
本文仅用作学习记录和交流