322. 零钱兑换(中等)



-
思路
- 由于题目提到 「每种硬币的数量是无限的」,所以这道题本质上完全背包问题,我直接使用了空间压缩的写法。
- dp[j] 表示当前区间在 [0, i]的硬币可以表示成 j 的最小数量。
- 注意,这里把 dp数组初始化为 amount+1 ,而不是 0,因为这道题要求的是最小值,如果初始化为 0,会导致
min(0, 正确答案) = 0,之所以取的是 amount+1 , 是因为这个值一定大于所有可能的组合方式,所以取最小值的时候一定不会是它。动态规划完成之后,如果结果仍然是这个值,说明不存在满足条件。 - 此外,还需要设置 dp[0] = 0,能够应对 amount = 0 的特殊情况。
-
代码
class Solution { public: int coinChange(vector<int>& coins, int amount) { int n = coins.size(); vector<int> dp(amount+1, amount+1); dp[0] = 0; for(int i=1; i<=n; ++i){ for(int j=1; j<=amount; ++j){ if(j >= coins[i-1]){ dp[j] = min(dp[j], dp[j-coins[i-1]] + 1); } } } if(dp[amount] >= amount+1) dp[amount] = -1; return dp[amount]; } }; -
收获
- 终于能够自己做出来背包问题了,但是这道题我将 dp数组初始化为 0,导致情况较为繁琐,题解的过程简洁很多。








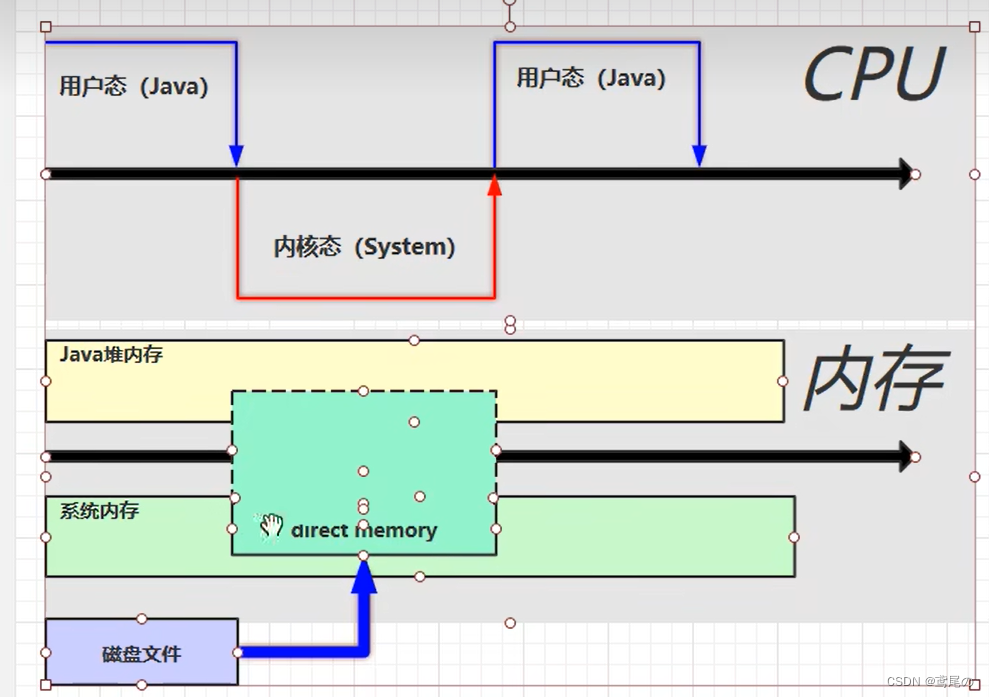

![[计算机图形学]光线追踪的基本原理(前瞻预习/复习回顾)](https://img-blog.csdnimg.cn/f25d83dfa92a4cacb27ca25bd2654f68.png)