一、光栅化的弊端

我们为什么要用光线追踪呢，在之前的篇章中，我们提到了，光栅化的方式很难表示一些全局的效果，如(1)软阴影，(2)Glossy的反射(类似镜子但又不像镜子那么光滑的材质，如打磨的铜镜和一些金属)，也就是光线弹射了两次的情况，(3)间接光照(不是由光源直接照亮而是由光源弹射多次后的光线照亮)。这些都是光栅化很难解决的。

光栅化和光线追踪的比较：

光栅化经常应用于一些实时渲染，也就是每秒要刷新30帧以上的画面，如游戏中需要根据玩家操控而导致画面实时的变化，因为光栅化相对于光线追踪运算量较小，所以速度也比较快，容易达到实时的效果。

而光线追踪常常应用于离线渲染，如高质量的电影，提前花大量的时间去渲染电影，最后到影院播放。一帧往往要花10KCPU小时，速度很慢，但质量非常高，接近真实的光影。

二、Whitted-Style光线追踪的基本思想

1.基本假设

在这里我们先做几个假设，尽管它们不一定严格地符合物理学。

1.光线是沿着直线传播的

2.光线与光线不会发生碰撞

3.光线是从光源被发出最后进入人的眼睛(光线可逆 )

2.基本思想

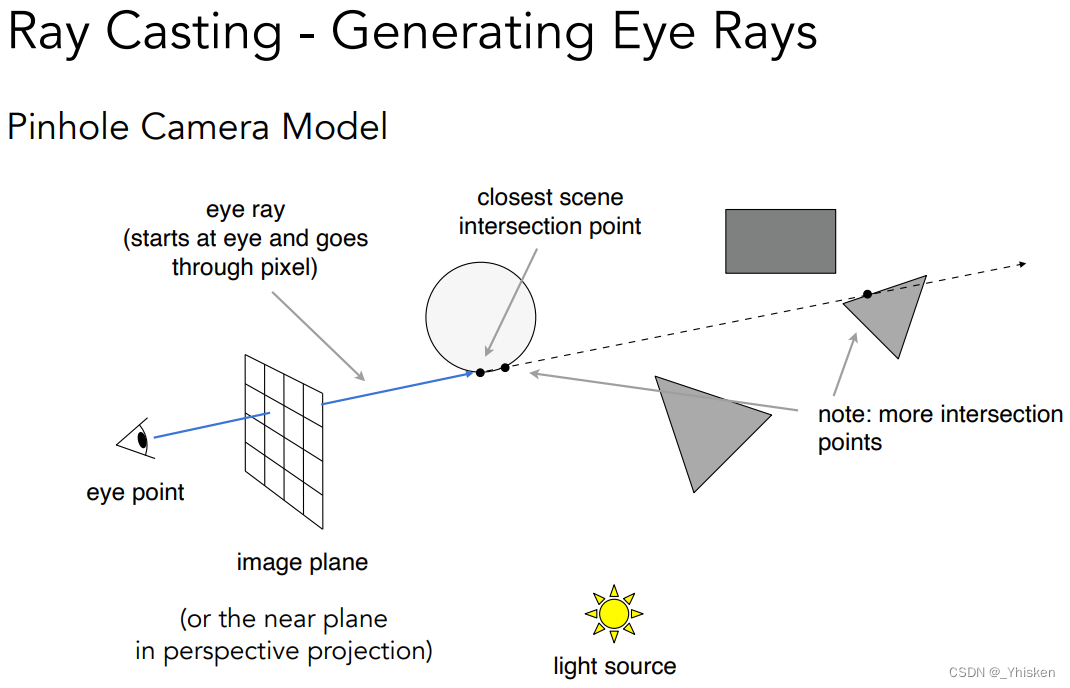
这里我们开始之前仍做几个假设：

1.相机是针孔摄像机 2.光源是点光源 3.发生的都是完美的反射/折射

光线追踪的第一步是从摄像机出发对着成像平面的一个像素发出一条光线，而穿过这个像素的光线会在场景中打到某个物体的某个位置，这个位置一定是离摄像机最近的，而这完美的解决了深度测试的问题，光线追踪使我们不需要深度缓存来测试深度。

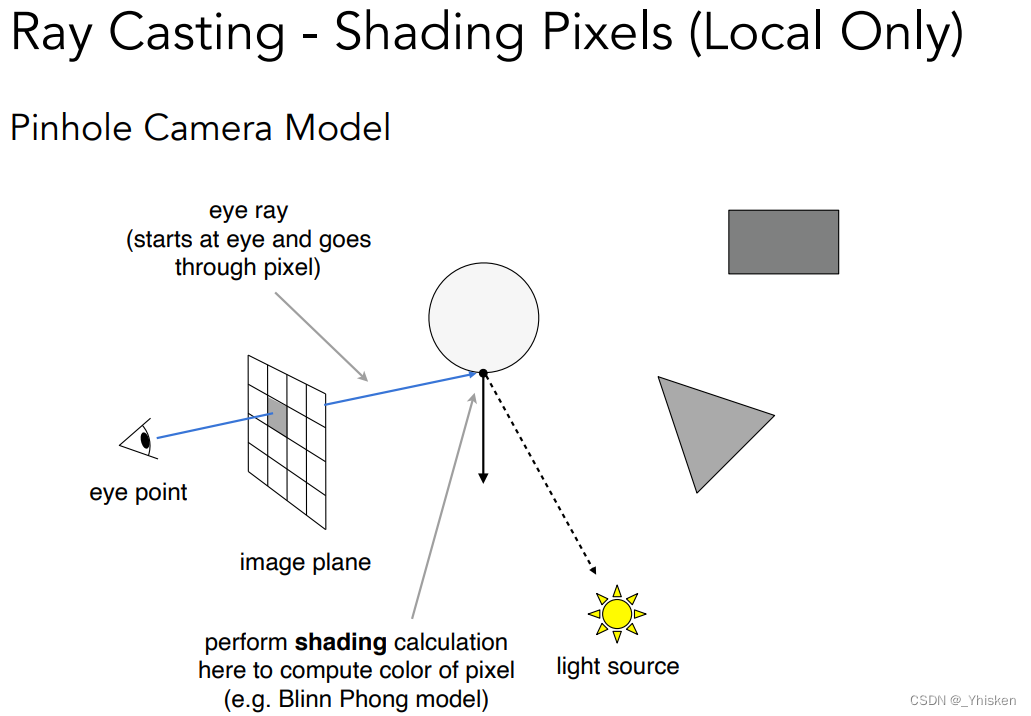
第二步则从被光线打到的点和光源连线，这条线(上图中虚线)叫做Shadow Ray，如果这条线中间没有物体遮挡则该点就是被光源照亮的点，否则说明该点在阴影中，最后通过着色模型计算颜色后就可以把这个点的颜色写入到像素中。

这就是最最基本的光线追踪，在早期人们通过这种方法来实现和光栅化近似的效果，但是这仍然不够，因为这仍然只考虑了光线的一次弹射。

这就要说到Whitted-Style光线追踪了，而这种方法实际上是一种递归思想，它考虑了光线的一次以上的弹射。和上面的思路类似，只不过我们考虑之后的多次弹射，如上图的玻璃球，眼睛发出的光线经过玻璃球之后发生了两次折射和一次反射，而这些光线又打到了场景中其它位置的点。我们把这些弹射点都和光源连线得到更多的Shadow Ray，然后判断这些点的可见性进行着色，而眼睛发出光线穿过的像素的颜色就由这些弹射点的着色加起来决定。这里我们也对眼睛发出的光线做出了分类，第一次弹射之前的光线叫做primary ray，之后弹射的都叫做secondary ray。

递归光线追踪得到的结果

三、光线的求交算法

上面的基本思路我们已经讲完了，接下来说一说如何计算光线与物体求交，这显然是一个数学问题，所以我们先把光线以数学的形式定义出来，光线就是一条射线，有一个起点o，有一个方向d(单位向量)，也就是上图点光源的表示可以表示为：r(t)=o+td，t始终是正的，也就是光线不能返回，也代表光线传播的距离。

1.最简单的情况

最简单的情况，计算光线与球相交，而球的三维定义也很简单，p也就是球上任何一个点，到原点c的距离始终相等。将光线带入球的方程求解即可。

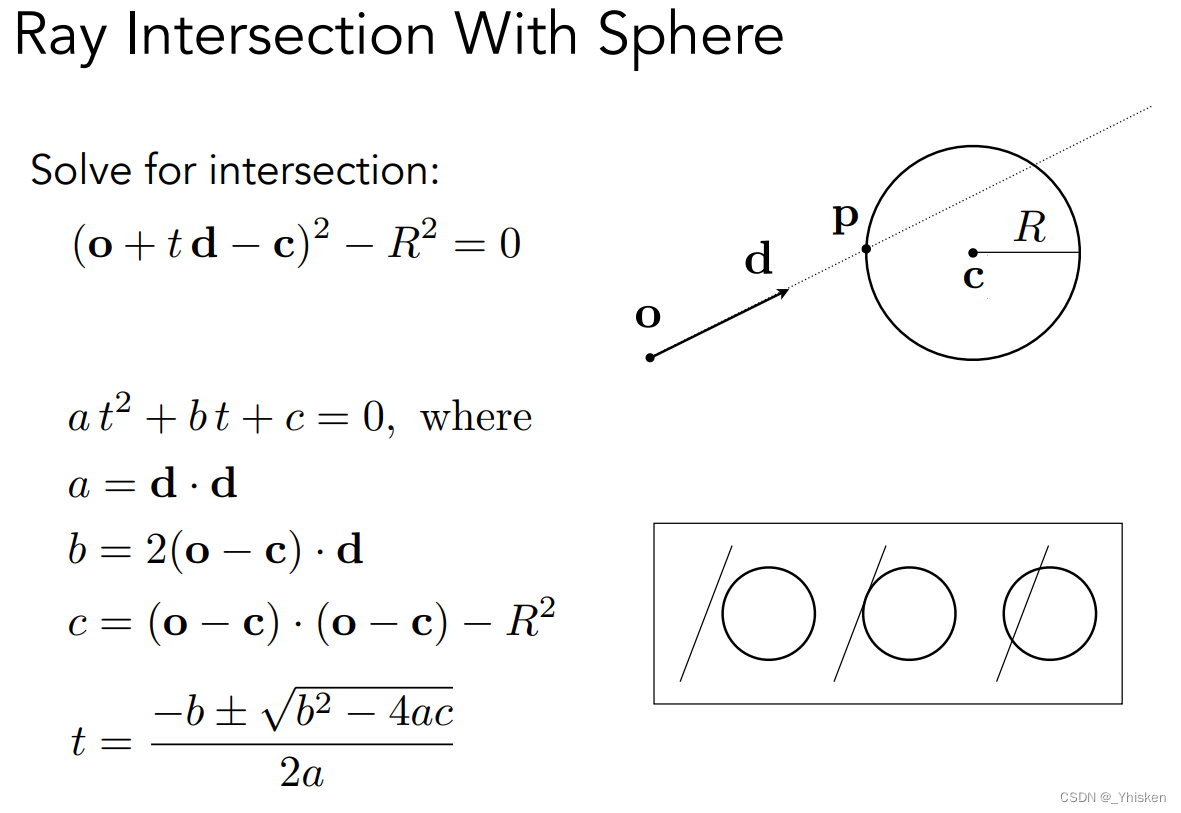
求根公式可以很容易的求出t，而t需要满足物理上的实际意义，也就是t>0，其次t是实数，这也就要求Δ≥0，最后根据两个t的取值，判定光线与球的相交/相切/相离。

2.光线与物体与隐式几何求交

介绍完了光线与球求交，我们也就可以推广到与一般的隐式表面求交。隐式表面都可以写成关于表面上点p的方程f(p)=0，而和之前的球一样，我们把光线带入方程，同样可以求出t。求出t仍然需要满足物理意义，大于0，是实数。解出的交点在哪呢？那就代回原光线方程，也就是o+td。

3.光线与显式几何求交(与空间中的三角形求交)

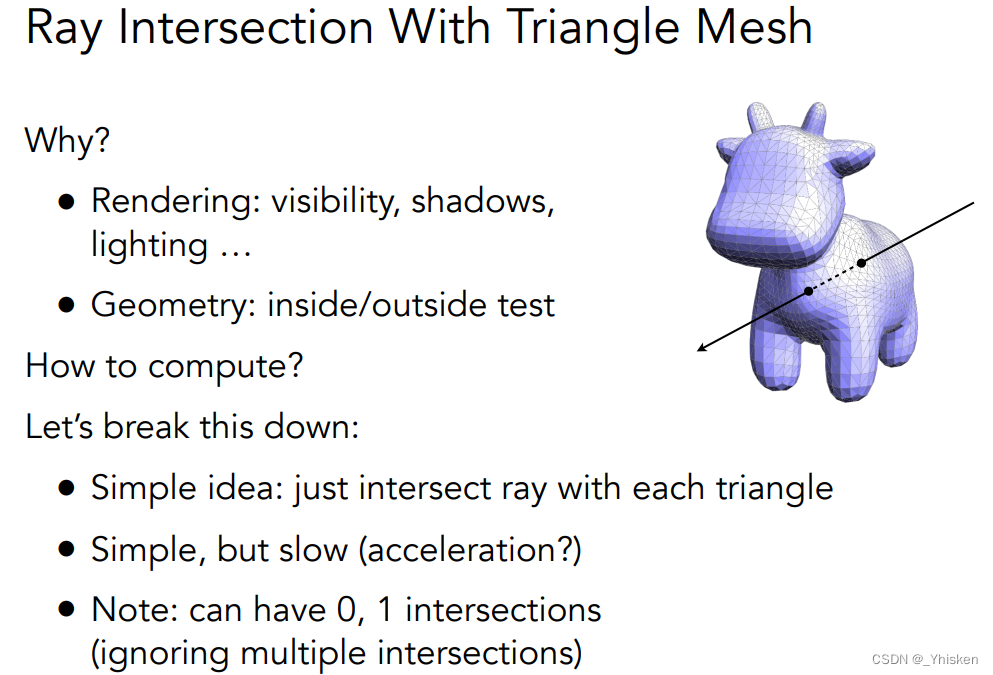
接下来讲如何计算光线与显式表面求交，那么最重要的显式表面是什么呢？当然是三角形网格了。而和三角形网格求交绕不开的话题就是如何计算光线与三角形求交。而通过光线与三角形求交，我们还可以判断光源在网格内还是外：从光源出发一条射线，如果能穿过网格两次，那么它一定在网格外，而如果只穿过一次，那就说明它在网格内，当然前提是网格是封闭的。

(1)一般求解算法

那么如何计算光线和三角形网格的求交呢？最简单的情况，把每个三角形都和光线判断一次有没有交点，求出很多个交点，取t最小的。但是问题是一个网格往往有上万个三角形，而我们的屏幕现在又基本都是1920x1080的分辨率，如此庞大的计算量会导致非常慢，那么在这其中人们发明了一些加速结构，能加速这里的计算，这里我们放到下一篇加速结构中介绍。

而现在我们暂时不考虑加速，就用这种穷举法来做，一根光线和一个三角形要么有1个交点，要么有0个交点(不考虑平行情况)。

首先，三角形一定在一个平面内，因为三个点确定一个平面。于是人们想到了一种方法，先做光线与平面求交，得到交点之后再判断交点在不在三角形内。而点在三角形内的判断我们之前光栅化那篇已经讲过了。

我们同样先把平面用数学形式表示出来(光线的表示仍然为o+td)，而平面可以用一个平面的法线和平面上的一个点唯一确定出来。也就是说平面上任意一点p'到p这个向量与定义的法线N都垂直，也就是点积为0。而显然，如果是平面外一点与p'的连线，它不与法线N垂直。而如果将这些量都以坐标代入，就会得到ax+by+cz+d=0，也就是一个平面的方程。

有了上面的准备，我们就可以计算光线与平面的求交了，同样的代入方程，即该点既在光线上又在平面上。同样的，我们可以解出t，同样的确保t≥0，且t为实数。

(2)Möller Trumbore算法

Möller Trumbore算法是一种更为快速的计算光线与三角形求交的算法，它没有分为两个步骤，而是直接计算光线是否与三角形有交点。这个算法用到了重心坐标，也就是说把三角形面上的点用重心坐标表示然后和光线方程联立求解，而每个坐标恰好又是三个分量x，y，z，我们需要求解的也是三个未知量t，b1，b2，三个方程三个未知数，这显然是一个线性方程组，我们用克莱姆法则很容易求解。而求解得出的t，同样需要大于0，那么如何判断求出的点是否在三角形内呢？我们前面讲重心坐标的时候讲到过，如果一个点在三角形内，那么它重心坐标下的三个分量都应该非负，也就是说b1，b2，1-b1-b2这三个量要≥0。