…

🌳🌲🌱本文已收录至：数据结构 | C语言
更多知识尽在此专栏中！

🎉🎉🎉欢迎点赞、收藏、关注 🎉🎉🎉

---

🌳前言

复杂度是衡量一个算法好坏的标准，可以从 时间 和 空间 两个维度进行比较。可能你之前听说某个算法的时间复杂度是O(N)，空间复杂度是O(1)，知道这是一个还不错的算法，那么你知道这些复杂度是如何计算出来的吗？本文将会揭开它们神秘的面纱，让你拥有一把衡量算法好坏的度量衡。

🌳正文

先说结论

• 时间复杂度主要是衡量一个算法的运行快慢，通常由循环决定
• 空间复杂度主要是衡量一个算法运行所需的额外空间，通常由开辟的空间大小决定

常见错误理解

• 时间复杂度是就是一段代码实际运行运行所花的时间。这种理解是错误的，因为环境的不同会导致代码运行的快慢，比如将一个大型程序放在你电脑上运行，和放在神威·太湖之光上运行所花的时间是肯定不同的，为了统一评判，我们将算法中基本操作的执行次数，称为算法的时间复杂度
• 空间复杂度和代码长度有关，代码码越长越复杂。错误，假如我们只创建了常数个变量，纵使代码写的再长，这个算法的空间复杂度也是O(1)，在程序中创建的变量个数(在内存中申请的空间大小)，称为空间复杂度，创建的变量数越多，算法所占空间就越复杂

当然这只是最基本的知识，关于时间&空间复杂度的更多知识可以往下看

---

🌲时间复杂度

🌱先说概念

在计算机科学中，算法的时间复杂度是一个函数，它定量地描述了该算法的运行时间

同大多数读者一样，我也不喜欢冗长复杂的官方解释，通俗来说，算法中基本操作的执行次数(循环部分)，就是代表了该算法的时间复杂度，比如下面这段代码

//请问这段代码的时间复杂度是多少？
int main()
{
    int N = 0;
    scanf("%d", &N);
    int count = 0;
    int i = 0;
    for (i = 0; i < N; i++)
    {
        count++;
    }
    return 0;
}

直接看循环部分，可以看到这个算法会循环N次，N是可变的，因此这个算法的时间复杂度就是N，简单吧，当然这只是一个最简单的例子，真实的程序循环比这复杂得多，此时就需要一个工具：大O渐进表示法，来帮助我们计算出算法的时间复杂度

🌱大O渐进表示法

大O符号：是用来描述函数渐进行为的数学符号，这个符号有点像数学中取极限
大O渐进表示法 的推导步骤：

1. 去掉已求出时间中的常数项。如果都是常数项，就用常数1代表时间复杂度
   • 比如时间为 2N ^ 2 + 2N + 100，需要去掉常数项100
2. 取出其中的最高阶项。比如 N、2N与N ^ 2，最高阶项为N^2
   • 接着上面的推导 2N ^ 2 + 2N，显而易见 2N ^ 2 要大于 2N，2N ^ 2就是这里的最高阶项
3. 如果存在常数项 * 最高阶项的情况，就要去除常数项。比如2N，最终复杂度为N
   • 最后在对最高阶项进行处理 2N ^ 2 ，常数项 2 对整体时间复杂度影响是不大的，应该去除

以上就是通过 大O渐进表示法 求时间复杂度的步骤，当然示例中的时间复杂度最终为O(N ^ 2)

大O渐进表示法 这样表示，是否合理呢？
答：很合理，尤其是放在计算机上使用

首先假设存在这么一个时间复杂度(不用 大O渐进表示法 版)： F(N) = N^2 + 2 * N + 10
经过 大O渐进表示法 处理后，变成 F(N) = O(N^2)，让我们来测试一组数据：

N	F(N) = N^2+2*N+10	F(N) = O(N^2)	相差率
10	100+20+10 = 130	100	23%
100	10000+200+10 = 10210	10000	2%
10000	100020010	100000000	0.02%

显然，随着数据的不断增大，二者间的差距会越来越小，而经过 大O渐进表示法 计算后的时间复杂度，是更容易计算的，除非追求精确的数据，否则用 大O渐进表示法 是很合理的~
大O渐进表示法 的核心作用就是去除那些对结果影响不大的项

🌱示例

时间复杂度这一块有几个比较经典的题目需要掌握一下，学会使用 大O渐进表示法 求出时间复杂度

🪴题目一

// 计算Func1的时间复杂度？
void Func1(int N, int M)
{
    int count = 0;
    for (int k = 0; k < M; ++k)
    {
        ++count;
    }
    for (int k = 0; k < N; ++k)
    {
        ++count;
    }
    printf("%d\n", count);
}

答案：O(N + M)
因为这里有两次循环，并且 N 和 M 都是未知数，无法区分出谁是最高阶项，因此两个都取出，都没有带常数项，不做去除操作。综上 Func1 的时间复杂度就是 O(N + M)

🪴题目二

// 计算Func2的时间复杂度？
void Func2(int N)
{
    int count = 0;
    for (int k = 0; k < 100; ++k)
    {
        ++count;
    }
    printf("%d\n", count);
}

答案： O(1)
显然，这里需要循环100次，都是常数项，直接遵循推导步骤一，时间复杂度为 O(1)
这里只循环了100次，即使循环1k次、1w次，也都是常数项，一样是 O(1)

🪴题目三

//计算strchr的时间复杂度？
const char* strchr(const char* str, int character);

答案： O(N)
说明：strchr 是一个字符串寻找函数，作用是在字符串str中查找目标字符character
有三种情况：

1. 最好的情况，只找一次，此时的时间复杂度为 O(1)
2. 最坏的情况，没有目标字符，需要把整个字符串找一遍，时间复杂度为 O(N)
3. 平均的情况，在中间就找到了，时间复杂度是 O(N / 2)

面对这种多分支情况，我们要做预期管理，用最悲观的态度来判断程序，这样做的好处是预期值低，结果出来时不会有很大落差，生活中也可以像这样，做好准备。言归正传，这里选择最坏的情况，即 O(N)，当然这种情况比较特殊，值得注意一下

🪴题目四

//计算BubbleSort的时间复杂度？
//冒泡排序
void BubbleSort(int* a, int n)
{
    assert(a);
    for (size_t end = n; end > 0; --end)
    {
        int exchange = 0;
        for (size_t i = 1; i < end; ++i)
        {
            if (a[i - 1] > a[i])
            {
                Swap(&a[i - 1], &a[i]);
                exchange = 1;
            }
        }
        if (exchange == 0)
            break;
    }
}

答案： O(N ^ 2)
冒泡排序是一个神奇的算法，每次冒泡比较的趟数都不同，可以这样推导

• 第一趟：比较 N - 1 次
• 第二趟：比较 N - 2 次
• 第三趟：比较 N - 3 次
• …………
• 最后一趟： 比较 1 次

总共比较的次数，就是时间复杂度，即 (N - 1) + (N - 2) + …… + 1，显然这是一个首项为 N - 1，尾项为 1 的等差数列，并且共有 N - 1 项，把高中学的知识用起来，N - 1 项和为 (N - 1) * N / 2 ,通过 大O渐进表示法 进行计算，最终结果为 O(N ^ 2)

🪴题目五

//计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x)
{
    assert(a);
    int begin = 0;
    int end = n - 1;
    // [begin, end]：begin和end是左闭右闭区间，因此有=号
    while (begin <= end)
    {
        int mid = begin + ((end - begin) >> 1);
        if (a[mid] < x)
            begin = mid + 1;
        else if (a[mid] > x)
            end = mid - 1;
        else
            return mid;
    }
    return -1;
}

答案： O(logN)
折半查找，一个站在巨人肩膀上的算法，假如我们想在世界范围内找一个人(假设有70亿人，且数据已排序)，通过二分查找，最多只需要查找33次，就能找出这个人，厉害吧？下面是二分查找的推导过程
假设需要查找的次数为 k 次，那么可以这样写

1. N / 2 -> N / 2 ^ 1
2. N / 4 -> N / 2 ^ 2
3. N / 8 -> N / 2 ^ 3

• …………

其中，左边的序号就是查找的次数 k ，可得出式子 N = 2 ^ k ，稍微变换下，得到 k = logN，其中第二个式子就是二分查找的时间复杂度，可能细心的人能发现，我没有写底数 2，不是不写，而是不好写，除非文本编辑器支持插入数学式，否则这个是很难表示的，鉴于这个东西应用的广泛性，有这样一个规定：在底数为 2 时，可以不写底数；如果底数为其他数，就需要写出来，其他底数都很少见的。 在有的地方，会把 lgN 看作 logN，第一种方法是有歧义的，和以 10 为底的对数表示形式一致，这是不太好的，但如果我们看到了，要明白 lgN 也是一个以 2 为底的对数
二分查找为何厉害？因为二分查找在计算时，每次都是对半查找，即 2 ^ k，是一个指数爆炸级查找，因此很快就能找到目标数，听说过一张纸对折64次就能碰到月球的故事吧？指数爆炸是个很庞大的数据

🪴题目六(递归)

//计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{
    if (N < 3)
        return 1;
    return Fib(N - 1) + Fib(N - 2);
}

答案： O(2 ^ N)
递归本来就是一个很麻烦的东西，更何况这是计算斐波那契数列

• 递归中的时间复杂度，计算的是每次递归中执行次数的累加

我们可以将递归斐波那契数列水平展开，即 1+2+4+8+16+32+……+2^N
根据 大O渐进表示法 ，去除影响小的常数项，最终结果为 O(2 ^ N)

相信你看完这些经典例题后，能对 大O渐进表示法 有一个新的认识，加油，你会越来越强的！

---

🌲空间复杂度

🌱照例，先说概念

算法的空间复杂度是指临时占用储存空间大小的量度

简单理解，空间复杂度是算法中变量的个数(申请的空间大小)。因为变量在使用前，要先声明，而声明会在内存中开辟空间，无论是在堆上还是栈上，都会造成内存损耗，损耗越大，空间复杂度就越高 ，先看代码：

//空间复杂度
int main()
{
	int a = 1;
	int b = 2;
	int c = 3;
	return 0;
}

看变量个数，有a、b、c三个变量，属于常数次，所以这个程序的空间复杂度是 O(1)，空间复杂度也遵循大O渐进表示法，这里就不再介绍了，忘记了的同学可以往上翻翻

• 当出现函数调用时，形参部分空间不计入空间复杂度的计算，递归除外，递归会建立额外的函数栈帧
  • 函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定
• 大多数情况下，算法的空间复杂度是 O(1) 或 O(N)

眼看千遍，不如手过一遍，下面跟着我一起来看看试题，练练手吧！

🌱示例

🪴题目一

//计算Fibonacci的空间复杂度？
//返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
    if (n == 0)
        return NULL;
    long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
    fibArray[0] = 0;
    fibArray[1] = 1;
    for (int i = 2; i <= n; ++i)
    {
        fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
    }
    return fibArray;
}

答案： O(N)
先看题目，这是一个迭代实现的斐波那契数列，没有使用递归，直接看看创建的变量个数：

1. fibArray
2. (n+1) * sizeof(long long)
3. i

共计申请了三块空间，其中第二块空间最大，为最高阶项，即 n + 1，去除常数项，最终结果为 O(N)

🪴题目二(递归)

//计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
    if (N == 0)
        return 1;
    return Fac(N - 1) * N;
}

答案： O(N)
递归的规则是 先递出，再回归，如果中途遇到递归，继续递出，因此在计算递归的空间复杂度时，计算的是每次递归调用的变量个数相加(所开辟的空间)，也可以看作递归的深度
显然这里的递归深度是 N，开辟了N个栈帧，每个栈帧使用了常数个空间，空间复杂度自然就是 O(N) 了

你学会了吗？是不是感觉空间复杂度要比时间复杂度简单些？毕竟现在是大容量时代，内存都变得不值钱了，于是对空间的要求自然而然的变低了。

---

🌲各种复杂度量级展示

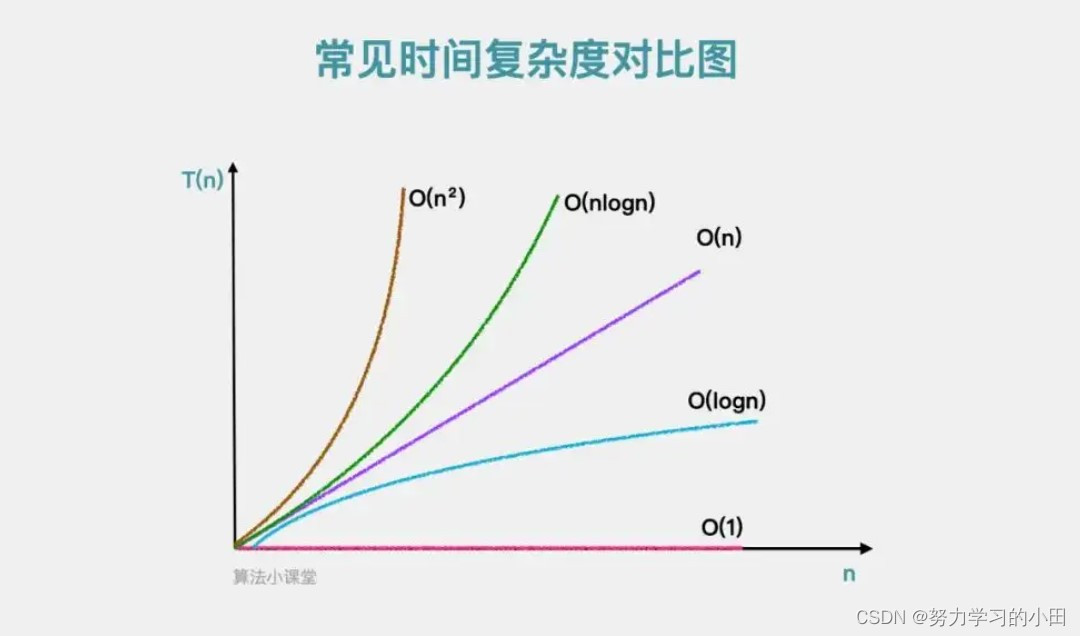
一般算法的常见复杂度类型如图所示

• 
  这是各种复杂度的关系图
  可以看到二分查找 logN 是真的强！
• 

---

🌲相关题目推荐

有些题目中，对时间复杂度和空间复杂度是有要求的，比如下面这两个简单题，用来练手就很不错，动起来吧！关于这两题的题解，后续会发布的

• 题目一：消失的数字 1

  • 

• 题目二：旋转数组 2

  • 

---

🌳总结

以上就是本次关于时间复杂度和空间复杂度的全部内容了，作为数据结构中的第一课，算是比较偏向于理论的部分，学起来也还比较简单，开胃菜嘛，等后面手撕顺序表、链表、二叉树就爽了

如果你觉得本文写的还不错的话，期待留下一个小小的赞👍，你的支持是我分享的最大动力！

如果本文有不足或错误的地方，随时欢迎指出，我会在第一时间改正

…

相关文章推荐
你真的了解时间复杂度吗
如何计算时间复杂度
时间复杂度计算 例题合集