例题来源:侯忠生教授的《无模型自适应控制:理论与应用》(2013年科学出版社)。
对应书本 4.2 单输入单输出系统(SISO)紧格式动态线性化(CFDL)的无模型自适应控制(MFAC)
例题4.1
题目要求

matlab代码
clc; clear all;
%% 期望轨迹
for k = 1:1:1000
if k<=300
yd(k) = 0.5*(-1)^round(k/500);
elseif 300<k & k<=700
yd(k) = 0.5*sin(k*pi/100)+0.3*cos(k*pi/50);
else
yd(k) = 0.5*(-1)^round(k/500);
end
end
plot(1:1000, yd,'r');
ylim([-1.5,1.5]);
hold on
%% MFAC参数设置
epsilon = 1e-5; % 伪偏导重置阈值
eta = 1; % 伪偏导增益
miu = 2; % 伪偏导步长
rho = 0.6; % 控制律增益
lambda = 2; % 控制律步长
u(1:2)=0;
y(1)=-1;
y(2)=1;
phi(1)=2;
for k = 2:1:999
%% 伪偏导更新
if k==2
delta_u = 0;
else
delta_u = u(k-1) - u(k-2);
end
phi(k) = phi(k-1) + eta * delta_u * (y(k) - y(k-1)- phi(k-1) * delta_u)/(miu + delta_u^2);
% 伪偏导重置
if abs(phi(k))<=epsilon | delta_u<= epsilon | sign(phi(k))~=sign(phi(1))
phi(k) = phi(1);
end
%% 控制律更新
u(k) = u(k-1) + rho*phi(k)*(yd(k+1)-y(k)) / (lambda + phi(k)^2);
%% 系统函数
if k<=500
y(k+1) = y(k)/(1+y(k)^2) + u(k)^3;
else
y(k+1) = ((y(k)*y(k-1)*y(k-2)*u(k-1)*(y(k-2)-1)+round(k/500)*u(k)))/(1+y(k-1)^2+y(k-2)^2);
end
end
plot(1:1000, y,'b');
ylim([-1.5,1.5]);
legend('y_d','y');
运行结果
λ
\lambda
λ 为 2 时:
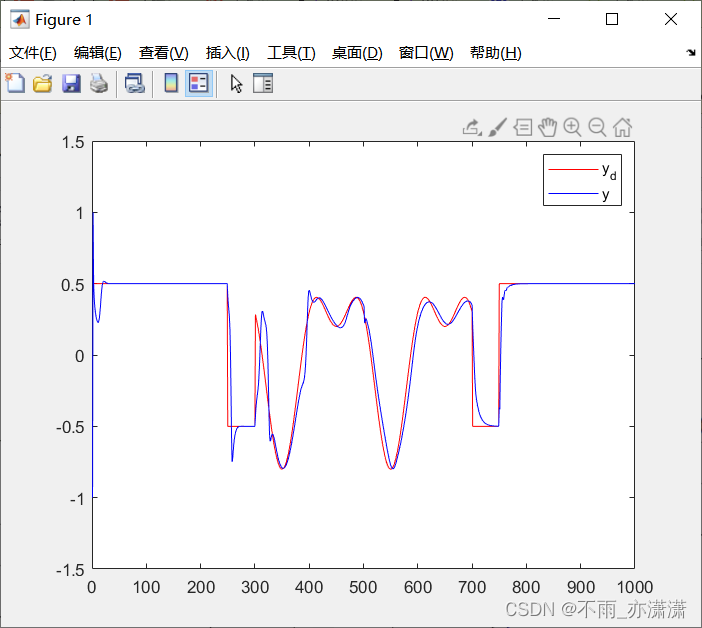
λ
\lambda
λ 为 0.1 时:
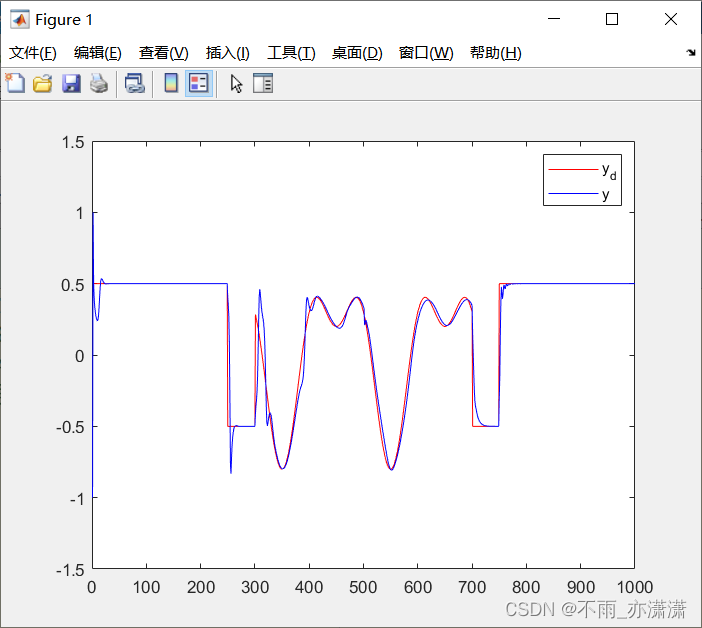
不同
λ
\lambda
λ 对比:
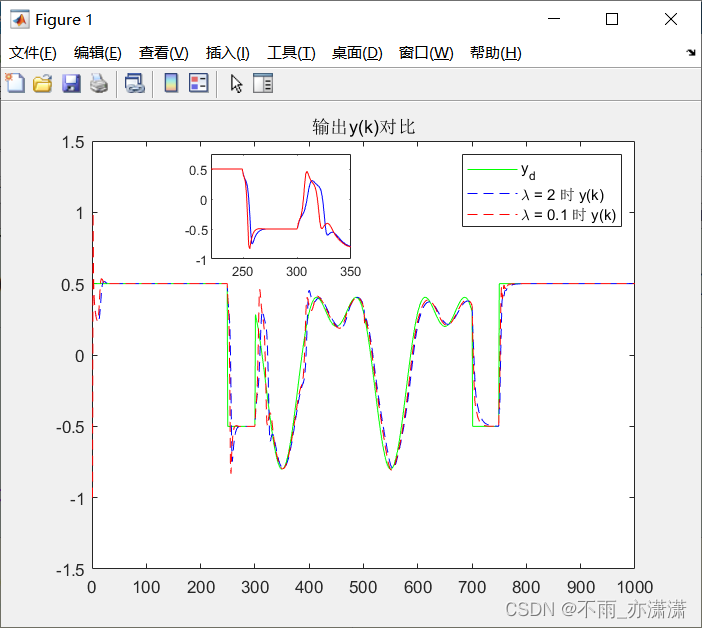
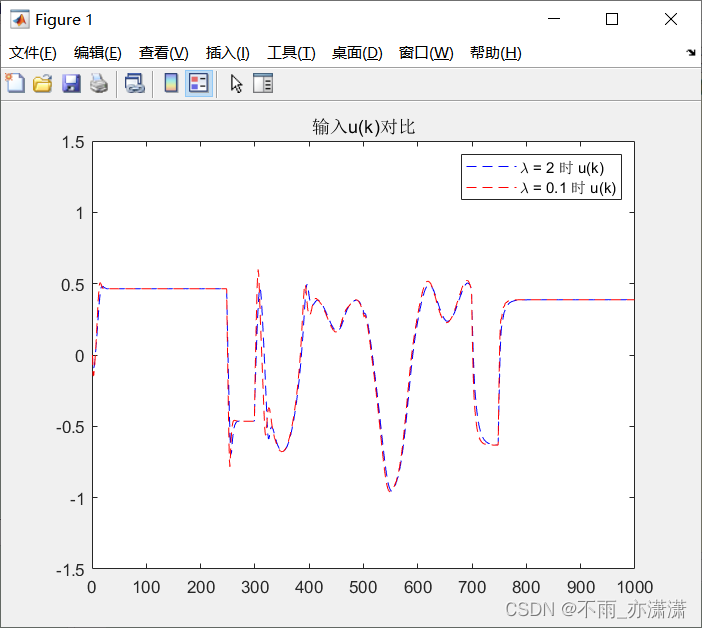
λ \lambda λ 减小,闭环响应速度变快,但超调也变大。
仔细观察一下书上的图4.1(a),运行结果和书本的不太一样,原因是书本给的期望输出信号公式中的 r o u n d ( k / 500 ) round(k/500) round(k/500) 实际上用了 r o u n d ( k / 100 ) round(k/100) round(k/100) ,估计是笔误,不过这些都是小问题啦,例题只是用来帮助理解原理的,参数变了没关系!

例题4.2
题目要求


matlab代码
clc; clear all;
%% 期望轨迹
for k = 1:1:1000
if k<=300 | k> 700
yd(k) = 5*sin(k*pi/50) + 2*cos(k*pi/100);
else
yd(k) = 5*(-1)^round(k/100);
end
end
plot(1:1000, yd,'r');
ylim([-1.5,1.5]);
hold on
%% MFAC参数设置
epsilon = 1e-5; % 伪偏导重置阈值
eta = 1; % 伪偏导增益
miu = 2; % 伪偏导步长
rho = 0.6; % 控制律增益
lambda = 2; % 控制律步长
u(1:2)=0;
y(1)=-1;
y(2)=1;
phi(1)=2;
for k = 2:1:999
%% 伪偏导更新
if k==2
delta_u = 0;
else
delta_u = u(k-1) - u(k-2);
end
phi(k) = phi(k-1) + eta*delta_u*(y(k)-y(k-1)-phi(k-1)*delta_u)/(miu + delta_u^2);
% 伪偏导重置
if abs(phi(k))<=epsilon | delta_u<= epsilon | sign(phi(k))~=sign(phi(1))
phi(k) = phi(1);
end
%% 控制律更新
u(k) = u(k-1) + rho*phi(k)*(yd(k+1)-y(k)) / (lambda + phi(k)^2);
%% 系统函数
if k==2
y(k+1) =0;
elseif k<=500
y(k+1) = 5*y(k)*y(k-1)/(1+y(k)^2+y(k-1)^2+y(k-2)^2) + u(k) + 1.1*u(k-1);
else
y(k+1) = 2.5*y(k)*y(k-1)/(1+y(k)^2+y(k-1)^2)+1.2*u(k)+1.4*u(k-1)+0.7*sin(0.5*(y(k)+y(k-1)))*cos(0.5*(y(k)+y(k-1)));
end
end
plot(1:1000, y,'b');
ylim([-15,15]);
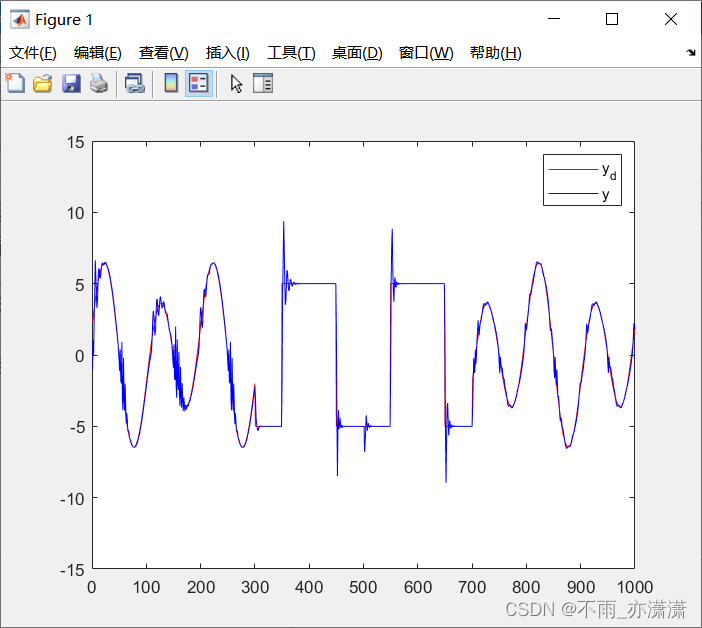
legend('y_d','y');
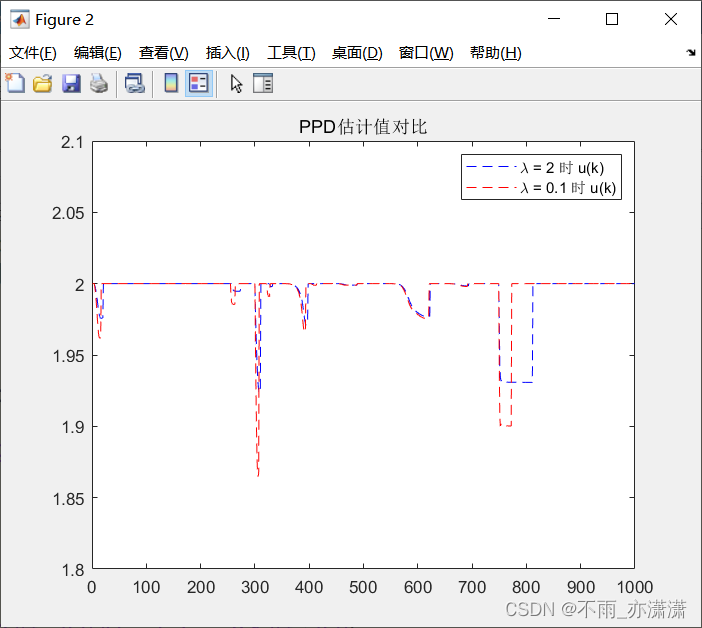
运行结果
λ \lambda λ 为 2 时:
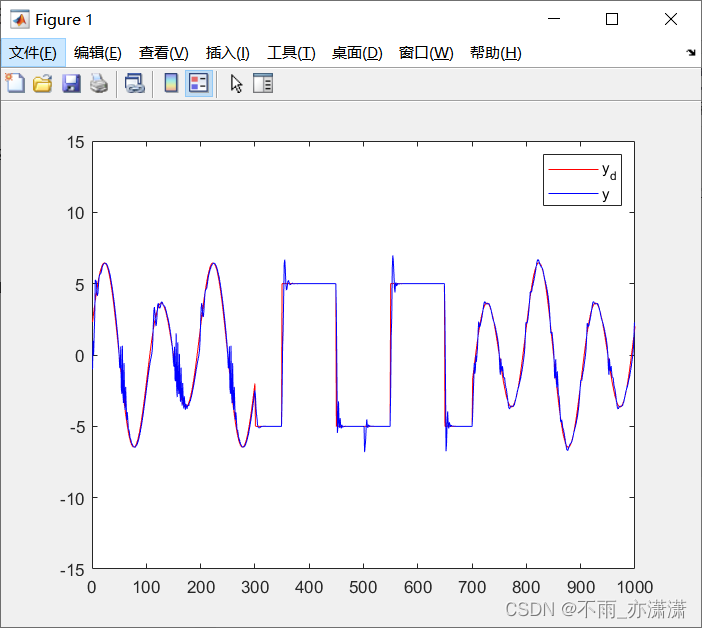
λ \lambda λ 为 0.1 时: