问：逻辑斯蒂回归是一种典型的线性回归模型。

答：正确。逻辑斯蒂回归是一种典型的线性回归模型。它通过将线性回归模型的输出结果映射到[0,1]区间内，表示某个事物发生的概率，从而适用于二分类问题。具体地说，它使用sigmoid函数对线性回归模型的输出进行映射，使得输出值在[0,1]范围内，表示概率大小。因此，逻辑斯蒂回归可以被看作是将线性回归模型扩展到离散输出的一种方法，属于广义线性模型的范畴。

逻辑回归的模型引入了sigmoid函数映射，是非线性模型，但本质上又是一个线性回归模型，因为除去sigmoid映射函数关系，其他的步骤，算法都是线性回归的。可以说，逻辑回归，都是以线性回归为理论支持的。
这里讲到的线性，是说模型关于系数一定是线性形式的

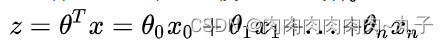
加入sigmoid映射后，变成：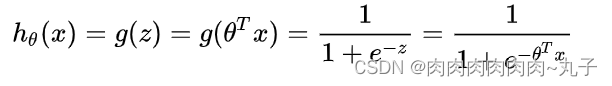 

如果分类平面本身就是线性的，那么逻辑回归关于特征变量x，以及关于系数都是线性的
如果分类平面是非线性的，例如题主提到的，那么逻辑斯蒂回归关于变量x是非线性的，但是关于参数仍然是线性的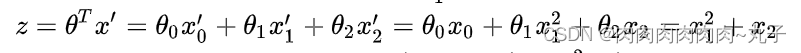 

这里，我们做了一个关于变量x的变换：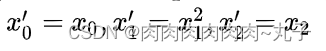 

其他非线性超平面一样的道理，我们可以通过变量的变化，最终一定可以化成形如

提到了SVM，区别是，SVM如果不用核函数，也得像逻辑回归一样，在映射后的高维空间显示的定义非线性映射函数,而引入了核函数之后，可以在低维空间做完点积计算后，映射到高维 

综上，逻辑回归本质上是线性回归模型，关于系数是线性函数，分离平面无论是线性还是非线性的，逻辑回归其实都可以进行分类。对于非线性的，需要自己去定义一个非线性映射。