文章目录
- 一:图像中的噪声
- (1)图像噪声分类
- (2)图像噪声的数学模型
- (3)程序
- 二:空间域平滑滤波
- (1)均值滤波
- A:均值滤波原理
- B:示例
- C:分析
- D:程序
- (2)高斯滤波
- A:高斯函数
- B:高斯滤波原理
- C:程序
- (3)中值滤波
- A:中值
- B:中值滤波原理
- C:示例
- D:中值滤波形状
- E:程序
- (4)双边滤波
- A:原理
- B:程序
图像平滑(Image Smoothing):是一种数字图像处理技术,用于减少图像中的噪声和不规则性,使图像更加平滑和连续。在图像中,噪声通常表现为不规则的、突出的像素值,这可能会导致图像细节丢失,使其难以进行分析和处理。图像平滑技术可以通过对像素值进行滤波来平滑图像,去除这些噪声

图像平滑主要分为如下两类
- 空域法: 主要借助模板运算,在像素点邻域内,利用噪声像素点特性进行滤波
- 频域法: 指对图像进行正交变换,利用噪声对应高频信息的特点进行滤波
一:图像中的噪声
图像中的噪声:是指在图像中出现的不希望出现的、随机的像素值变化,这些变化可能是由于图像采集设备、传输通道或者图像处理过程中引入的。噪声会使图像中出现不规则的亮度、色彩等异常情况,从而导致图像质量下降,给后续的分析和处理带来困难。也可以理解为真实信号与理想信号之间存在的偏差。噪声通常以二维函数 n ( x , y ) n(x,y) n(x,y)来表示

(1)图像噪声分类
图像噪声分类:
- 高斯噪声: 高斯噪声是最常见的一种图像噪声,其像素值变化符合正态分布。在图像中,高斯噪声通常表现为细小的均匀噪声
- 椒盐噪声: 椒盐噪声是一种随机的噪声,其表现为图像中出现黑白像素点,通常是由于图像传输或采集设备的问题引起的
- 周期噪声: 周期噪声是指在图像中出现周期性的波纹、条纹等形式的噪声,这通常是由于摄像机、扫描仪等采集设备的问题引起的
- 色彩噪声: 色彩噪声是指在图像中出现的颜色偏差,这通常是由于相机传感器的颜色误差、照明条件不足等原因引起的
另外,图像噪声可以根据信号和噪声的关系分为
- 加性噪声: 加性噪声与图像信号不相关,也即 g ( x , y ) = f ( x , y ) + n ( x , y ) g(x,y)=f(x,y)+n(x,y) g(x,y)=f(x,y)+n(x,y)
- 乘性噪声: 乘性噪声与图像信号相关,也即 g ( x , y ) = f ( x , y ) + f ( x , y ) n ( x , y ) g(x,y)=f(x,y)+f(x,y)n(x,y) g(x,y)=f(x,y)+f(x,y)n(x,y)
在信号变化很小时,往往将乘性噪声近似认为加性噪声,而且总是假定信号和噪声互相独立
(2)图像噪声的数学模型
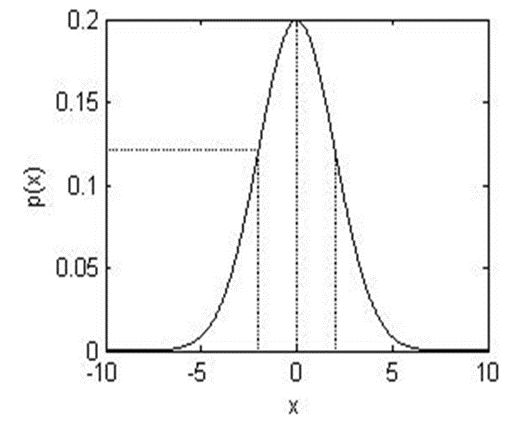
高斯噪声:定义为高斯噪声信号 x x x的概率密度函数
- μ \mu μ:噪声 x x x的均值或期望值
- σ \sigma σ:噪声 x x x的标准差
p
(
x
)
=
1
2
π
σ
e
−
(
x
−
μ
)
2
/
2
σ
2
p(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-(x-\mu)^{2} / 2 \sigma^{2}}
p(x)=2πσ1e−(x−μ)2/2σ2
当
x
x
x服从高斯分布时,其值有70%落在
[
(
μ
−
σ
)
,
(
μ
+
σ
)
]
[(\mu-\sigma),(\mu+\sigma)]
[(μ−σ),(μ+σ)]范围内,且有95%落在
[
(
μ
−
2
σ
)
,
(
μ
+
2
σ
)
]
[(\mu-2\sigma),(\mu+2\sigma)]
[(μ−2σ),(μ+2σ)]
椒盐噪声:定义椒盐噪声信号 x x x有效模型
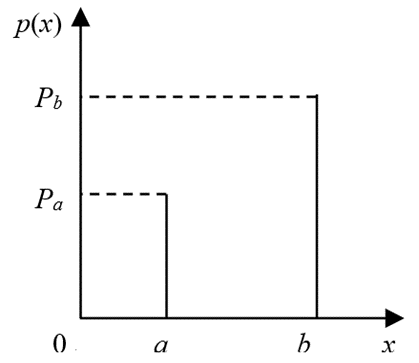
p ( x ) = { P a x = a P b x = b 0 otherwise p(x)=\left\{\begin{array}{cc}P_{a} & x=a \\P_{b} & x=b \\0 & \text { otherwise }\end{array}\right. p(x)=⎩ ⎨ ⎧PaPb0x=ax=b otherwise
如下图
- 当 P a = 0 , P b ≠ 0 P_{a}=0,P_{b} \not=0 Pa=0,Pb=0时,表现为“盐”噪声
- 当 P a ≠ 0 , P b = 0 P_{a}\not=0,P_{b} =0 Pa=0,Pb=0时,表现为“胡椒”噪声
可以看出,高斯噪声和椒盐噪声不同分布特性
- 椒盐噪声:噪声幅值基本相同,出现位置随机
- 高斯噪声:噪声出现位置是分布在每一像素 点上,幅度值是随机的,分布近似符合高斯 正态特性
(3)程序

imnoise函数:用于在图像中添加噪声的函数,可以模拟在图像采集、传输、处理等过程中引入的不同类型的噪声。imnoise函数的常见语法格式如下
J = imnoise(I, type)
J = imnoise(I, type, parameters)
其中,I是输入图像,type是噪声类型,可以是字符串形式的字符向量或枚举型变量,parameters是可选的参数,用于控制噪声的强度、分布等。imnoise函数支持以下类型的噪声
gaussian:高斯噪声,可选参数包括mean(均值)和var(方差)salt & pepper:椒盐噪声,可选参数包括density(密度)poisson:泊松噪声,无可选参数speckle:乘性噪声,可选参数包括mean(均值)和var(方差)localvar:局部方差噪声,可选参数包括二维数组w(窗口大小)和二维数组var(局部方差)lognormal:对数正态分布噪声,可选参数包括mean(均值)和var(方差)rayleigh:瑞利分布噪声,可选参数为scale(尺度)erlang:伽马分布噪声,可选参数包括shape(形状)和scale(尺度)uniform:均匀分布噪声,可选参数包括lower(下限)和upper(上限)
matlab实现:
Image = mat2gray( imread('original_pattern.jpg') ,[0 255]);
noiseIsp=imnoise(Image,'salt & pepper',0.1); %添加椒盐噪声,密度为0.1
imshow(noiseIsp,[0 1]); title('椒盐噪声图像');
noiseIg=imnoise(Image,'gaussian'); %添加高斯噪声,默认均值为0,方差为0.01
figure;imshow(noiseIg,[0 1]); title('高斯噪声图像');
Python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像
img = cv2.imread('original_pattern.jpg', cv2.IMREAD_GRAYSCALE)
# 将图像归一化到 [0,1] 范围内
img = cv2.normalize(img.astype('float'), None, 0.0, 1.0, cv2.NORM_MINMAX)
# 添加椒盐噪声,密度为 0.1
noiseIsp = img.copy()
noiseIsp = np.random.choice([0, 1], size=noiseIsp.shape, p=[0.9, 0.1]).astype('float') * 255
noiseIsp = cv2.merge([noiseIsp, noiseIsp, noiseIsp])
noiseIsp = cv2.cvtColor(noiseIsp, cv2.COLOR_BGR2GRAY)
noiseIsp = cv2.normalize(noiseIsp.astype('float'), None, 0.0, 1.0, cv2.NORM_MINMAX)
# 显示椒盐噪声图像
plt.imshow(noiseIsp, cmap='gray', vmin=0, vmax=1)
plt.title('椒盐噪声图像')
plt.show()
# 添加高斯噪声,默认均值为 0,方差为 0.01
noiseIg = cv2.randn(img.shape, 0, 0.01)
noiseIg = cv2.add(img, noiseIg)
# 将图像归一化到 [0,1] 范围内
noiseIg = cv2.normalize(noiseIg.astype('float'), None, 0.0, 1.0, cv2.NORM_MINMAX)
# 显示高斯噪声图像
plt.imshow(noiseIg, cmap='gray', vmin=0, vmax=1)
plt.title('高斯噪声图像')
plt.show()
二:空间域平滑滤波
空间域平滑滤波:是数字图像处理中常用的一种滤波方法,也被称为模糊滤波。它通过对图像像素周围一定大小的邻域内像素灰度值进行加权平均,以消除图像中的高频噪声和细节信息,从而使图像变得更加平滑。常见有以下几种
- 均值滤波
- 高斯滤波
- 中值滤波
- 双边滤波
(1)均值滤波
A:均值滤波原理
均值滤波:是以某一像素为中心,在它的周围选择一邻域,将邻域内所有点的均值(灰度值相加求平均)来代替原来像素值
- S S S:以点 ( x , y ) (x,y) (x,y)为中心的邻域
- M M M:领域 S S S内总像素数目
g ( x , y ) = 1 M ∑ ( m , n ) ∈ S f ( m , n ) g(x, y)=\frac{1}{M} \sum_{(m, n) \in S} f(m, n) g(x,y)=M1(m,n)∈S∑f(m,n)
如下为常用的线性平滑简单均值模板
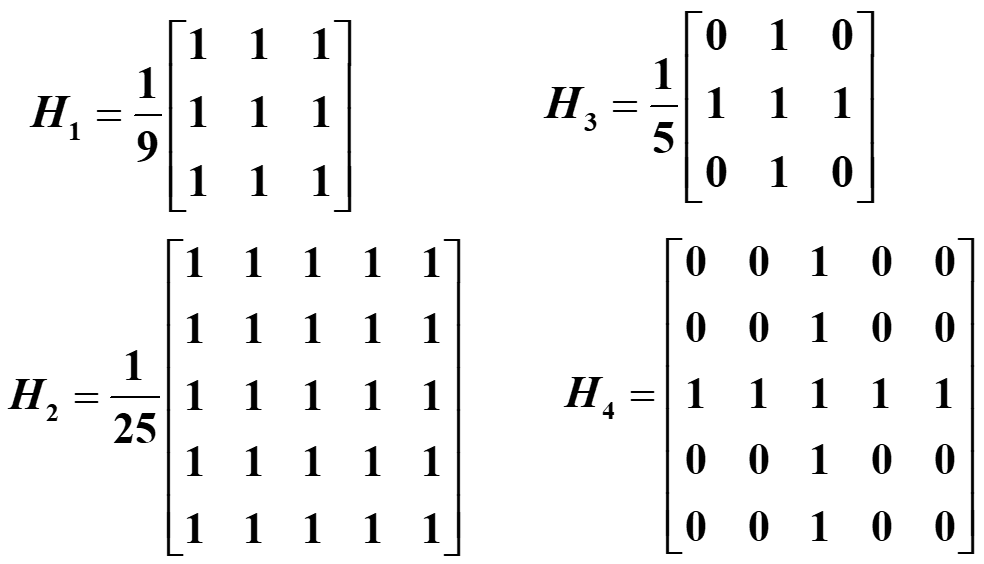
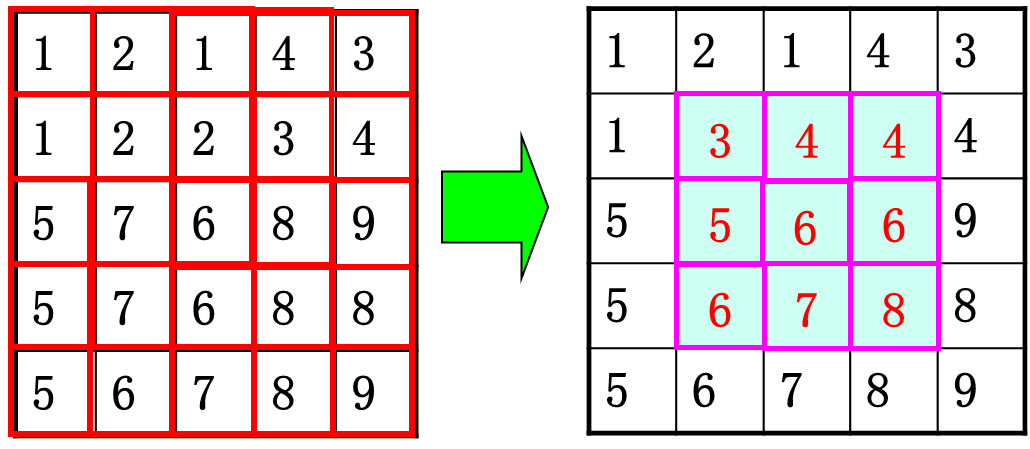
B:示例
如下图
C:分析
均值滤波的优点是简单易实现,对于一些噪声较小的图像能够取得不错的平滑效果。但是,它也存在一些缺点。例如,它会对图像中的边缘和细节信息造成模糊,同时也可能使得一些噪声点变得更加明显。此外,均值滤波对于椒盐噪声等高斯分布以外的噪声类型效果较差
- 若邻域内存在噪声,经过平均,噪声幅度会大为降低
- 点与点之间的灰度差值变小,边缘和细节处变得模糊
- 邻域半径越大,图像模糊程度越厉害
D:程序

fspecial函数:用于生成一些常见的滤波器卷积核的函数。这些卷积核可以用于各种图像处理任务,例如平滑、锐化、边缘检测等。fspecial 函数返回一个二维的卷积核矩阵 H,该矩阵的大小和形状由参数 type 和可选参数决定。可以将该卷积核作为参数传递给 MATLAB 中的卷积函数,如 conv2 函数,对图像进行滤波操作。该函数语法如下
H = fspecial(type, varargin)
其中,参数 type 指定了要生成的卷积核的类型。type 可以取以下字符串值:
'average':平均滤波器;'disk':圆形平滑滤波器;'gaussian':高斯滤波器;'laplacian':拉普拉斯滤波器;'log':高斯-拉普拉斯(LoG)滤波器;'motion':运动模糊滤波器;'prewitt':Prewitt 滤波器;'sobel':Sobel 滤波器
filter函数:是一个二维滤波器函数,用于对图像进行滤波操作。它可以使用用户自定义的滤波器卷积核进行滤波,也可以使用 fspecial 函数生成的预定义滤波器卷积核进行滤波。函数返回一个滤波后的二维数组 B,其大小和形状由参数 shape 决定。可以将 filter2 函数用于图像处理任务,例如平滑、锐化、边缘检测等。需要注意的是,filter2 函数的滤波操作是基于卷积运算实现的,因此需要对输入的图像进行填充,以避免边缘像素的影响。可以使用 MATLAB 中的 padarray 函数对图像进行填充。该函数语法如下
B = filter2(h, A, shape)
其中,参数 h 是一个二维滤波器卷积核,参数 A 是一个需要进行滤波的二维数组(通常是图像),shape 是一个可选参数,用于指定输出数组的大小和形状
- 当
shape为same时:输出数组的大小与输入数组相同,但是边缘可能会受到卷积核的影响而变化 - 当
shape为full时:输出数组的大小为输入数组大小与卷积核大小之和减去1,输出数组的边缘受卷积核影响而扩展 - 当
shape为valid时,输出数组的大小为输入数组大小与卷积核大小之差加1,输出数组的边缘不受卷积核影响
imfilter函数:是一个通用的二维滤波器函数,用于对图像进行滤波操作。它可以使用用户自定义的滤波器卷积核进行滤波,也可以使用 fspecial 函数生成的预定义滤波器卷积核进行滤波。imfilter 函数返回一个滤波后的二维数组 B,其大小和形状由参数 options 决定。可以将 imfilter 函数用于图像处理任务,例如平滑、锐化、边缘检测等。该函数语法如下
B = imfilter(A, h, options)
其中,参数 A 是一个需要进行滤波的二维数组(通常是图像),参数 h 是一个二维滤波器卷积核,options 是一个包含滤波选项的结构体,可选参数包括:
'conv':指定卷积操作;'corr':指定相关操作;'same':指定输出大小与输入相同;'full':指定输出大小为输入大小加上滤波核大小减一;'valid':指定输出大小为输入大小减去滤波核大小加一;'replicate':指定用边缘值来填充图像;'symmetric':指定用对称方式来填充图像;'circular':指定用循环方式来填充图像
matlab实现:
Image=imread('Letters-a.jpg');
noiseI=imnoise(Image,'gaussian'); %添加高斯噪声
subplot(221),imshow(Image),title('原图');
subplot(222),imshow(noiseI),title('高斯噪声图像');
result1=filter2(fspecial('average',3),noiseI); %3×3均值滤波
result2=filter2(fspecial('average',7),noiseI); % 7×7均值滤波
subplot(223),imshow(uint8(result1)),title('3×3均值滤波');
subplot(224),imshow(uint8(result2)),title('7×7均值滤波');
Python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像
img = cv2.imread('Letters-a.jpg')
# 添加高斯噪声
noise_img = cv2.GaussianBlur(img, (5, 5), 0)
# 显示原图和噪声图像
plt.subplot(221), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title('原图')
plt.subplot(222), plt.imshow(cv2.cvtColor(noise_img, cv2.COLOR_BGR2RGB)), plt.title('高斯噪声图像')
# 3x3均值滤波
result1 = cv2.blur(noise_img, (3, 3))
# 7x7均值滤波
result2 = cv2.blur(noise_img, (7, 7))
# 显示3x3和7x7均值滤波结果
plt.subplot(223), plt.imshow(cv2.cvtColor(result1, cv2.COLOR_BGR2RGB)), plt.title('3×3均值滤波')
plt.subplot(224), plt.imshow(cv2.cvtColor(result2, cv2.COLOR_BGR2RGB)), plt.title('7×7均值滤波')
plt.show()
(2)高斯滤波
A:高斯函数
高斯函数:高斯函数是一种连续的、平滑的、钟形曲线函数,用于表示在统计和概率领域中连续随机变量的概率密度函数。高斯函数在图像处理、信号处理、模式识别、机器学习等领域广泛应用
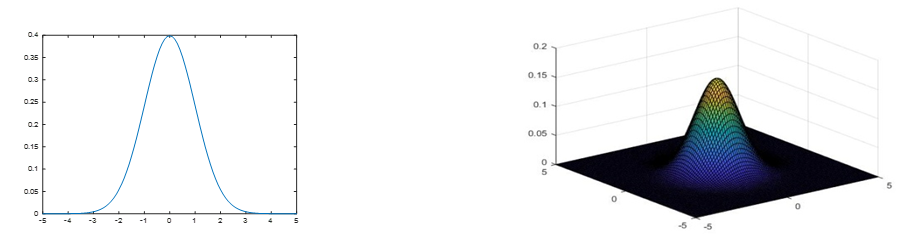
- 一维高斯函数: G ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 G(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} G(x)=σ2π1e−2σ2(x−μ)2。一维高斯函数的图像是一条钟形曲线,它的峰值位于均值处,随着 x x x增加或减小,函数值逐渐减小,且标准差越大,函数的宽度越大
- 二维高斯函数: G ( x , y ) = 1 2 π σ x σ y e − ( x − μ x ) 2 2 σ x 2 − ( y − μ y ) 2 2 σ y G(x, y)=\frac{1}{2 \pi \sigma_{x} \sigma_{y}} e^{-\frac{\left(x-\mu_{x}\right)^{2}}{2 \sigma_{x}^{2}}-\frac{\left(y-\mu_{y}\right)^{2}}{2 \sigma_{y}}} G(x,y)=2πσxσy1e−2σx2(x−μx)2−2σy(y−μy)2。 二维高斯函数的图像是一个二维钟形曲面,它的峰值位于 ( μ x , μ y ) (\mu_x,\mu_y) (μx,μy)处,随着 x x x或 y y y的增加或减小,函数值逐渐减小,且标准差越大,函数的宽度越大
在图像处理中,二维高斯函数通常用于进行图像平滑处理,即利用高斯函数的低通滤波性质,去除图像中的噪声和细节信息。同时,高斯函数还可以用于图像边缘检测、尺度空间分析等任务
B:高斯滤波原理
高斯滤波原理:是以某一像素为中心,在它的周围选择一个局部邻域,把邻域内像素的灰度按照高斯正态分布曲线进行统计,分配相应的权值系数,然后将邻域内所有点的加权平均值代替原像素值
g ( x , y ) = ∑ r = − k k ∑ s = − l l f ( x − r , y − s ) H ( r , s ) g(x, y)=\sum_{r=-k}^{k} \sum_{s=-l}^{l} f(x-r, y-s) H(r, s) g(x,y)=r=−k∑ks=−l∑lf(x−r,y−s)H(r,s)
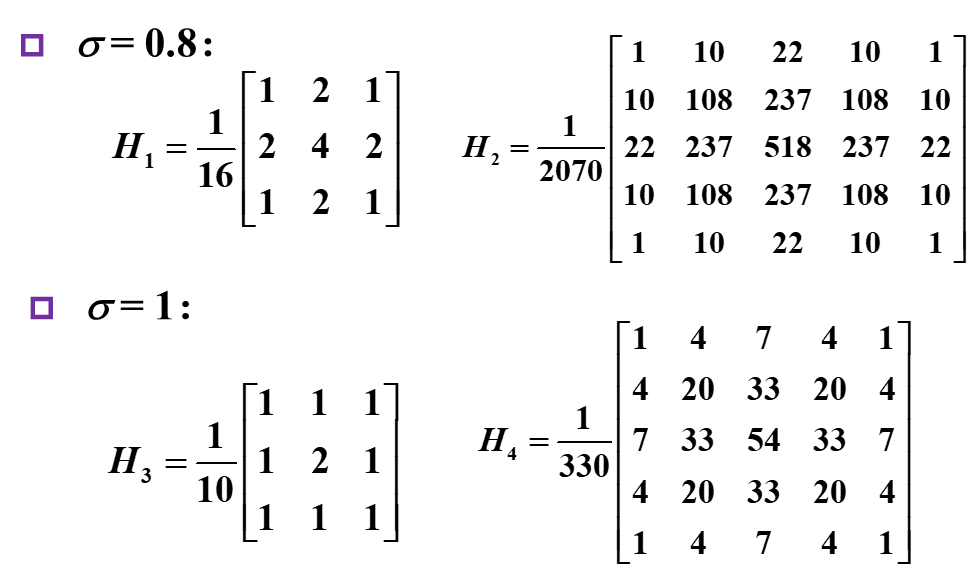
如下为典型的高斯模板
C:程序

matlab实现:
Image=imread('Letters-a.jpg');
sigma1=0.6; sigma2=10; r=3; % 高斯模板的参数
NoiseI= imnoise(Image,'gaussian'); %加噪
gausFilter1=fspecial('gaussian',[2*r+1 2*r+1],sigma1);
gausFilter2=fspecial('gaussian',[2*r+1 2*r+1],sigma2);
result1=imfilter(NoiseI,gausFilter1,'conv');
result2=imfilter(NoiseI,gausFilter2,'conv');
imshow(Image);title('原图');
figure;imshow(NoiseI);title('高斯噪声图像');
figure;imshow(result1);title('sigma1 =0.6高斯滤波');
figure;imshow(result2);title('sigma2 =10高斯滤波');
python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
Image = cv2.imread('Letters-a.jpg')
sigma1 = 0.6
sigma2 = 10
r = 3
NoiseI = cv2.imread('Letters-a.jpg', 0)
NoiseI = cv2.GaussianBlur(NoiseI, (3,3), 0)
NoiseI = cv2.addWeighted(NoiseI, 1.5, NoiseI, -0.5, 0)
gausFilter1 = cv2.getGaussianKernel(2*r+1, sigma1)
gausFilter1 = np.outer(gausFilter1, gausFilter1)
gausFilter2 = cv2.getGaussianKernel(2*r+1, sigma2)
gausFilter2 = np.outer(gausFilter2, gausFilter2)
result1 = cv2.filter2D(NoiseI, -1, gausFilter1)
result2 = cv2.filter2D(NoiseI, -1, gausFilter2)
plt.imshow(cv2.cvtColor(Image, cv2.COLOR_BGR2RGB))
plt.title('原图')
plt.show()
plt.imshow(NoiseI, cmap='gray')
plt.title('高斯噪声图像')
plt.show()
plt.imshow(result1, cmap='gray')
plt.title('sigma1 =0.6高斯滤波')
plt.show()
plt.imshow(result2, cmap='gray')
plt.title('sigma2 =10高斯滤波')
plt.show()
(3)中值滤波
A:中值
中值:一组数 x 1 , x 2 , . . . , x n x_{1},x_{2},...,x_{n} x1,x2,...,xn,把 n n n个数按值的大小顺序排列如下: x i 1 < x i 2 < . . . x i n x_{i_{1}}<x_{i_{2}}<...x_{in} xi1<xi2<...xin,则中值为
y = { x i ( n + 1 2 ) 1 2 [ x i ( n 2 ) + x i ( n 2 + 1 ) ] n 为奇数 n 为偶数 y=\left\{\begin{array}{l}x_{i\left(\frac{n+1}{2}\right)} \\\frac{1}{2}\left[x_{i\left(\frac{n}{2}\right)}+x_{i\left(\frac{n}{2}+1\right)}\right]\end{array}\right. n 为奇数 n 为偶数 y={xi(2n+1)21[xi(2n)+xi(2n+1)]n为奇数n为偶数
B:中值滤波原理
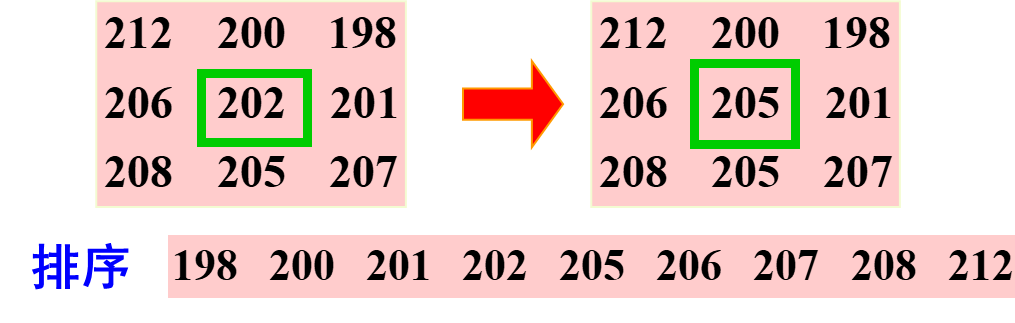
中值滤波原理:噪声的出现,使被处理点像素比周围像素亮(暗)许多。中值滤波则以被处理点为中心,选取一个邻域窗口,窗口内所有点值排序,取中值代替该点值
C:示例
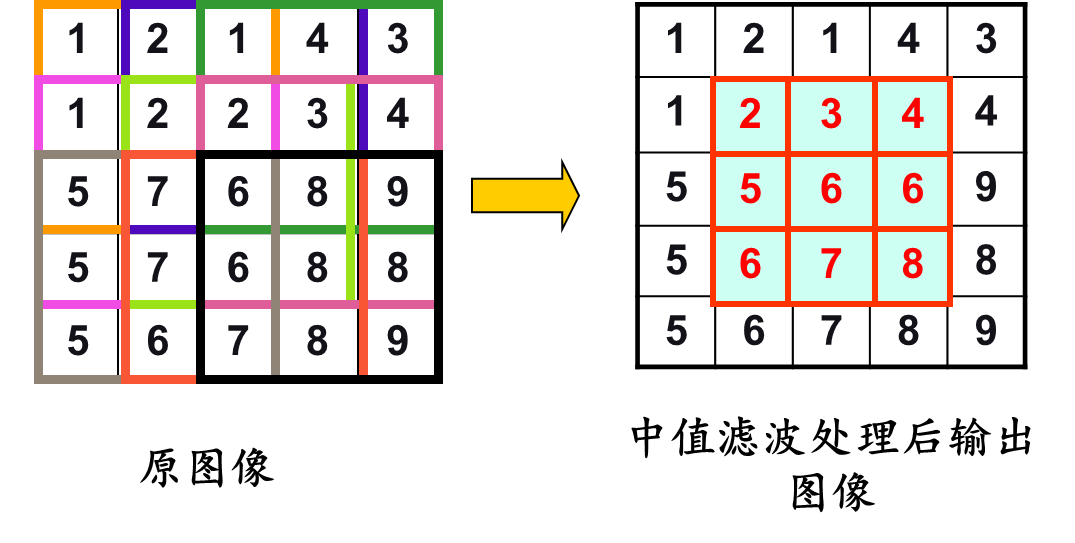
D:中值滤波形状


E:程序

medfilt2函数:是MATLAB中的一个二维中值滤波函数,用于对图像进行去噪处理。该函数语法如下
B = medfilt2(A, [M N])
B = medfilt2(A, [M N], 'symmetric')
B = medfilt2(A, [M N], 'indexed', P)
其中
A:输入的图像矩阵。[M N]:中值滤波器的大小,其中M和N分别表示滤波器在行方向和列方向的大小,必须为奇数,默认为[3 3]。'symmetric':指定对称性边界条件,即对边缘进行反射填充,默认为零填充。'indexed':指定输入图像的像素值采用整数标识,其中P是一个向量,其长度等于输入图像中可能出现的像素值的数量,向量中的值表示相应像素值的位置
matlab实现:
Image=rgb2gray(imread('lotus.bmp'));
noiseI=imnoise(Image,'salt & pepper',0.1);
imshow(noiseI),title('椒盐噪声图像');
result=medfilt2(noiseI); %3×3中值滤波
figure,imshow(uint8(result)),title('3×3中值滤波');
python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('lotus.bmp')
gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
noisy_img = cv2.addSaltAndPepper(gray_img, 0.1)
plt.imshow(noisy_img, cmap='gray')
plt.title('椒盐噪声图像')
plt.show()
result = cv2.medianBlur(noisy_img, 3)
plt.imshow(result, cmap='gray')
plt.title('3x3中值滤波')
plt.show()
(4)双边滤波
A:原理
双边滤波:“双边”意味着平滑滤波时不仅考虑邻域内像素的空间邻近性,而且要考虑邻域内像素的灰度相似性
B F [ I ] P = 1 W P ∑ q ∈ S G σ s ( ∥ p − q ∥ ) G σ r ( ∣ I p − I q ∣ ) I q W P = ∑ q ∈ S G σ s ( ∥ p − q ∥ G σ r ( ∣ I p − I q ∣ ) G σ s ( ∥ p − q ∥ ) = e ( ∥ p − q ∣ ) 2 2 σ s 2 G σ r ( ∣ I p − I q ∣ ) = e − ( I p − I q ) 2 2 σ r 2 \begin{array}{c}B F[I]_{P}=\frac{1}{W_{P}} \sum_{q \in S} G_{\sigma_{s}}(\|p-q\|) G_{\sigma_{r}}\left(\left|I_{p}-I_{q}\right|\right) I_{q} \\W_{P}=\sum_{q \in S} G_{\sigma_{s}}\left(\|p-q\| G_{\sigma_{r}}\left(\left|I_{p}-I_{q}\right|\right)\right. \\G_{\sigma_{s}}(\|p-q\|)=e^{\frac{(\| p-q \mid)^{2}}{2 \sigma_{s}^{2}}} G_{\sigma_{r}}\left(\left|I_{p}-I_{q}\right|\right)=e^{-\frac{\left(I_{p}-I_{q}\right)^{2}}{2 \sigma_{r}^{2}}}\end{array} BF[I]P=WP1∑q∈SGσs(∥p−q∥)Gσr(∣Ip−Iq∣)IqWP=∑q∈SGσs(∥p−q∥Gσr(∣Ip−Iq∣)Gσs(∥p−q∥)=e2σs2(∥p−q∣)2Gσr(∣Ip−Iq∣)=e−2σr2(Ip−Iq)2
B:程序

matlab实现:
Image=im2double(imread('girl.bmp'));
NoiseI= Image+0.05*randn(size(Image));
w=15; % 定义双边滤波窗口宽度
sigma_s=6; sigma_r=0.1; % 双边滤波的两个标准差参数
[X,Y] = meshgrid(-w:w,-w:w);
Gs = exp(-(X.^2+Y.^2)/(2*sigma_s^2));%计算邻域内的空间权值
[hm,wn] = size(NoiseI);
result=zeros(hm,wn);
for i=1:hm
for j=1:wn
temp=NoiseI(max(i-w,1):min(i+w,hm),max(j-w,1):min(j+w,wn));
Gr = exp(-(temp-NoiseI(i,j)).^2/(2*sigma_r^2));%计算灰度邻近权值
% W为空间权值Gs和灰度权值Gr的成绩
W = Gr.*Gs((max(i-w,1):min(i+w,hm))-i+w+1,(max(j-w,1):min(j+w,wn))-j+w+1);
result(i,j)=sum(W(:).*temp(:))/sum(W(:));
end
end
subplot(1,3,1),imshow(Image),title('原始图像');
subplot(1,3,2),imshow(NoiseI),title('随机噪声图像');
subplot(1,3,3),imshow(result),title('双边滤波图像');
python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像并将像素值转换为浮点数
Image = cv2.imread('girl.bmp', cv2.IMREAD_GRAYSCALE)
Image = cv2.normalize(Image.astype('float'), None, 0.0, 1.0, cv2.NORM_MINMAX)
# 添加高斯噪声
NoiseI = Image + 0.05 * np.random.randn(*Image.shape)
# 双边滤波
w = 15
sigma_s = 6
sigma_r = 0.1
X, Y = np.meshgrid(np.arange(-w, w+1), np.arange(-w, w+1))
# 计算邻域内的空间权值
Gs = np.exp(-(X**2 + Y**2) / (2 * sigma_s**2))
hm, wn = NoiseI.shape
result = np.zeros((hm, wn))
for i in range(hm):
for j in range(wn):
# 取出当前像素的邻域
temp = NoiseI[max(i-w, 0):min(i+w, hm), max(j-w, 0):min(j+w, wn)]
# 计算灰度邻近权值
Gr = np.exp(-(temp - NoiseI[i, j])**2 / (2 * sigma_r**2))
# W 为空间权值 Gs 和灰度权值 Gr 的乘积
W = Gr * Gs[max(i-w, 0):min(i+w, hm)-i+w+1, max(j-w, 0):min(j+w, wn)-j+w+1]
# 对 W 和邻域内像素值的乘积求和并除以 W 的和,得到当前像素的值
result[i, j] = np.sum(W * temp) / np.sum(W)
# 显示图像
plt.subplot(1, 3, 1)
plt.imshow(Image, cmap='gray')
plt.title('原始图像')
plt.subplot(1, 3, 2)
plt.imshow(NoiseI, cmap='gray')
plt.title('随机噪声图像')
plt.subplot(1, 3, 3)
plt.imshow(result, cmap='gray')
plt.title('双边滤波图像')
plt.show()