贝叶斯定理是关于随机事件 A 在 B 条件下发生的概率：

在贝叶斯定理中，每个名词都有约定俗成的名称：
· P(A|B)是已知 B 发生后 A 的条件概率
· P(A)是 A 的先验概率
· P(B|A)是已知 A 发生后 B 的条件概率

2.贝叶斯的推导
我们可以从条件概率的定义推导出贝叶斯定理。
根据条件概率的定义，在事件 B 发生的条件下事件 A 发生的概率为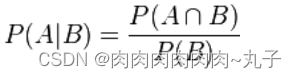

同样地，在事件 A 发生的条件下事件 B 发生的概率为：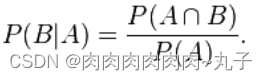

结合这两个方程式，我们可以得到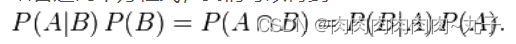

这个引理有时称作概率乘法规则。

上式两边同除以 P(A)，若P(A)是非零的，我们可以得到贝叶斯定理（ABABAB定理）:

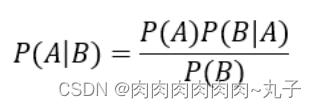
在这里我们已经获得基本的贝叶斯公式了，但是我在这里进行引入全概率公式，获得基本贝叶斯定理的展开式。
全概率公式：
若事件A1，A2 …… 满足

所以对任意事件B有

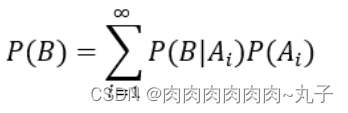
结合基本贝叶斯定理，获得贝叶斯定理的变式如下：

综上有：

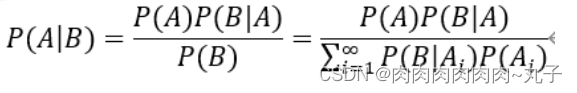
3.贝叶斯下的朴素贝叶斯

在上面已经获得贝叶斯定理的一个公式了，这时候我们结合机器学习对公式中的变量进行代替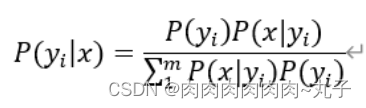

· x表示输入的特征
· y_i表示对输入的特征进行分类的结果
由于输入的P(x1,…,xn)是给定的常数值，我们可以得到以下式子： 

在分类问题中，对于输入的样本，实际上就是求取该样本在各各类别的概率，以获得该样本所属的类别。最终获得贝叶斯定理的简化形式，也就是朴素贝叶斯：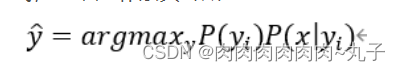 

那如何求先验概率P(y_i )和似然概率P(x│y_i )？
· 对于P(y_i )，sklearn.naive_bayes模块定义了三种方法
（1）对应类的占总数据集的占比，作为先验概率
（2）均值
（3）自己设定每一类别的先验概率

· 对于似然概率P(x│y_i )，在特征相互独立的情况下，根据y下x特征的分布情况进行求解
（1）y下x的分布是高斯分布

（2）y下x的分布是二项分布 

（3）y下x的分布是多项分布

二、朴素贝叶斯

代码如下（示例）：

"""
GaussianNB(【*, priors=None, var_smoothing=1e-09】)
"""
import numpy as np
import pandas as pd
from sklearn.naive_bayes import GaussianNB

np.random.seed(0)
x = np.random.randint(-5,5,size=(6,2))
y = np.array([0,0,0,1,1,1])
data = pd.DataFrame(np.hstack([x, y.reshape(-1,1)]), columns=['x1','x2','y'])
display(data)

gnb = GaussianNB()
gnb.fit(x,y)

## 属性
#每个类别样本的数量
print('样本数量：', gnb.class_count_)
#每个类别的先验概率
print('先验概率：', gnb.class_prior_)
#每个类别的标签
print('标签：', gnb.classes_)
#每个特征在每个类别下的方差
print('方差：',gnb.sigma_)
#每个特征在每个类别下的均值
print('均值：',gnb.theta_)

## 方法
x_test = np.array([[2,1]])
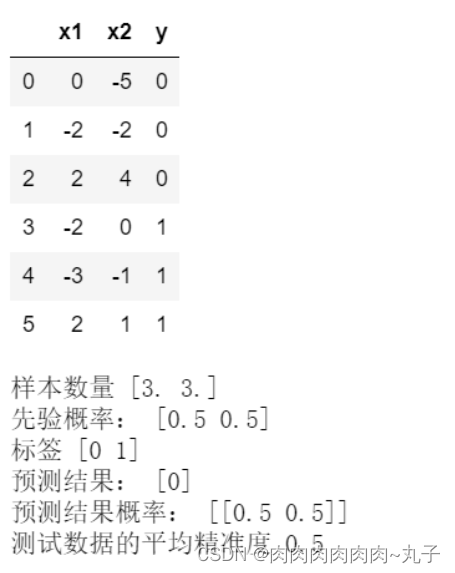
print('预测结果：', gnb.predict(x_test))
print('预测结果概率：', gnb.predict_proba(x_test))
print('测试数据的平均精准度',gnb.score(x,y))

2.伯努利朴素贝叶斯

代码如下（示例）：

"""
BernoulliNB(【*, alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None】) 
"""
from sklearn.naive_bayes import BernoulliNB

np.random.seed(0)
x = np.random.randint(-5,5,size=(6,2))
y = np.array([0,0,0,1,1,1])
data = pd.DataFrame(np.concatenate([x,y.reshape(-1,1)], axis=1), columns=['x1','x2','y'])
display(data)

bnb = BernoulliNB()
bnb.fit(x,y)

## 属性
print('样本数量',bnb.class_count_)
#每个类别样本所占的比重，即P(y)。注意该值为概率取对数之后的结果，
#如果需要查看原有的概率，需要使用指数还原。
print('先验概率：',np.exp(bnb.class_log_prior_))
print('标签',bnb.classes_)

## 方法
x_test = np.array([[2,1]])
print('预测结果：', bnb.predict(x_test))
print('预测结果概率：', bnb.predict_proba(x_test))
print('测试数据的平均精准度',bnb.score(x,y))

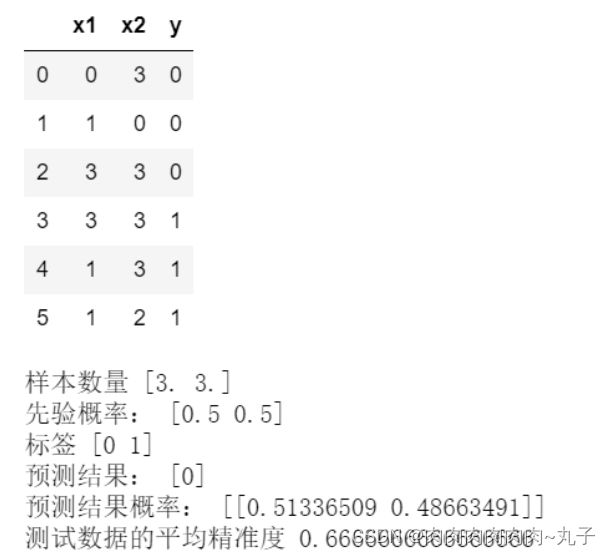
3.多项式朴素贝叶斯

代码如下（示例）：

"""
MultinomialNB(【*, alpha=1.0, fit_prior=True, class_prior=None】)
多项式朴素贝叶斯中各特征都是正数（类别），然而二项式朴素贝叶斯可以为负（实质上通过参数binarize划分01）
"""
from sklearn.naive_bayes import MultinomialNB

np.random.seed(0)
x = np.random.randint(0,4,size=(6,2))
y = np.array([0,0,0,1,1,1])
data = pd.DataFrame(np.hstack([x, y.reshape(-1,1)]), columns=['x1','x2','y'])
display(data)

mnb = MultinomialNB()
mnb.fit(x,y)

## 属性
print('样本数量',mnb.class_count_)
#每个类别样本所占的比重，即P(y)。注意该值为概率取对数之后的结果，
#如果需要查看原有的概率，需要使用指数还原。
print('先验概率：',np.exp(mnb.class_log_prior_))
print('标签',mnb.classes_)

## 方法
x_test = np.array([[2,1]])
print('预测结果：', mnb.predict(x_test))
print('预测结果概率：', mnb.predict_proba(x_test))
print('测试数据的平均精准度',mnb.score(x,y))

总结
朴素贝叶斯的主要优点有：

1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。

2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。

3）对缺失数据不太敏感，算法也比较简单，常用于文本分类。

朴素贝叶斯的主要缺点有：

1） 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。

3）由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。