快速找出满足所需比值的一对电阻值

快速找出满足所需比值的一对电阻值 - Python 函数实现

news2024/9/23 19:19:57

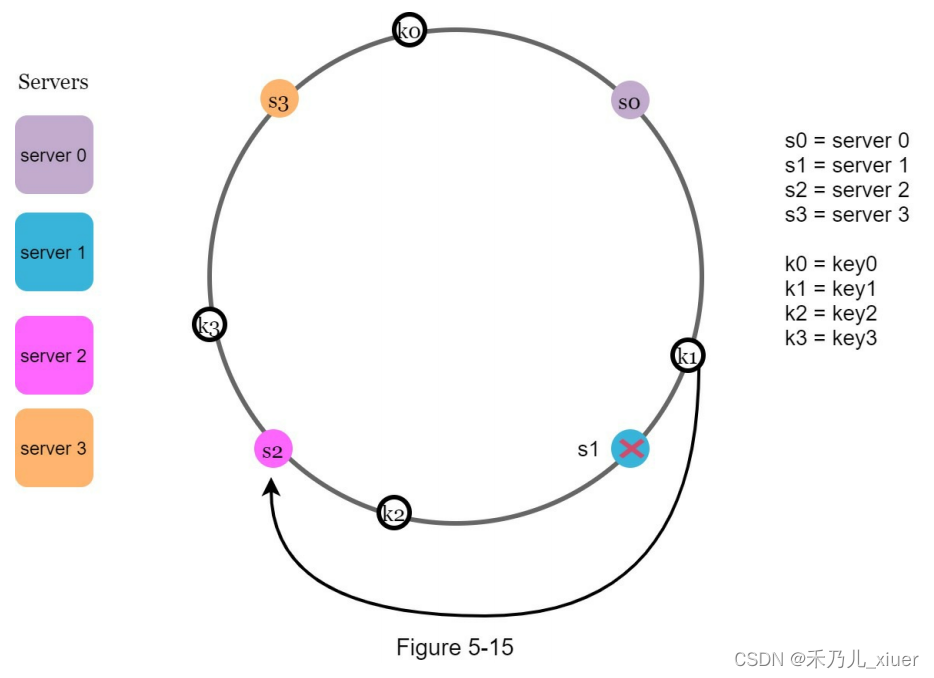
常用的5% 和1% 精度电阻的阻值满足E24 数系，基数只能在这个数系里取，再乘上10 的n 次幂。E24 数系如下图：

在这里插入图片描述
之前我都是人肉一个一个试的，凭运气挑，终于忍不住想整个一劳永逸的小工具。

代码

对于给定的比值，用一个python 函数暴力搜索，将所有正好满足比值的组合全部输出，如果没有正好等于的，就只返回一个偏差最小的组合，代码如下：

from typing import List, Tuple

def find_e24_resistor_pair(target_ratio: float) -> List[Tuple[float, float, float]]:
    """
    在 E24 优先数系中找到两个电阻值，使它们的比值最接近给定的比值。
    如果有多个解，返回所有较小值不相等且在 1~10 范围内的解。
    如果没有精确匹配的解，返回偏差最小的一组解。
    每个解都是一个三元组 (r1, r2, diff)，其中 r1 和 r2 是电阻值，diff 是偏差。

    :param target_ratio: 目标比值
    :return: 电阻值组合列表
    """
    e24 = [1.0, 1.1, 1.2, 1.3, 1.5, 1.6, 1.8, 2.0, 2.2, 2.4, 2.7,
            3.0, 3.3, 3.6, 3.9, 4.3, 4.7, 5.1, 5.6, 6.2, 6.8,
            7.5, 8.2, 9.1]
    result = []
    min_diff = float('inf')
    epsilon = 1e-9
    min_exponent = math.floor(math.log10(e24[0] * target_ratio))
    max_exponent = min_exponent + 1
    for r2 in e24:
        for r1_base in e24:
            for i in range(min_exponent, max_exponent + 1):
                r1 = r1_base * (10 ** i)
                ratio = r1 / r2
                diff = abs(ratio - target_ratio)
                if diff < epsilon:
                    result.append((r1,r2,diff))
                elif diff < min_diff:
                    min_diff = diff
                    min_result = (r1,r2,diff)
    if len(result) == 0:
        result.append(min_result)

    return result

这个函数的搜索过程是：先把分子r2 的取值范围固定在10 的0 次幂，也就是1.1， 1.2, … 9.1 这些E24 数系的基数，然后根据给定的比值，计算分母r1 的搜索范围，最后依次遍历分子和分母的所有取值组合。比如，若比值为5，分子最小值为1.0，最大9.1，则分母的取值范围是5 ~ 45.5，也就是10 的0 次幂到1 次幂，而且很显然，无论比值有多大，分母的最大值和最小值最多只能差一个数量级。

如果目标比值为3，这个函数会返回一个列表，里面是精确匹配的四个组合3 / 1、3.3 / 1.1 、3.6 / 1.2、3.9 / 1.3：

[
 (3.0, 1.0, 0.0), 
 (3.3, 1.1, 4.440892098500626e-16),
 (3.6, 1.2, 0.0),
 (3.9, 1.3, 0.0)
]

每组返回三个数字，第三个是偏差的绝对值。其中3.3 / 1.1 有点特殊，偏差并不等于0，这是因为浮点数的精度问题，如下：

>>> 3.3 / 1.1
2.9999999999999996

这个比值并不等于3。所以判断两个浮点数是否相等，不能像整数一样直接比较，而是要把两个浮点作差，如果差值足够小，就判断是相等。上面代码中的变量epsilon 就是这个足够小的差值，1e-9，偏差小于这个值就当0 来看。如果所需的比值为33.55，函数的返回结果是：

[(91.0, 2.7, 0.15370370370370523)]

没有正好匹配的组合，最接近的组合是91 / 2.7。偏差的绝对值是0.1537，误差比例是0.4591%，考虑到实际电阻值本身的误差也有1%，所以这个组合可以接受。再顺便加一个函数，直接把返回结果打印出来，方便使用：

def print_resistor_pair(target_ratio: float):
    resistors = find_e24_resistor_pair(target_ratio)
    if len(resistors) == 1 and resistors[0][2] > 1e-9:
        diff_ratio = resistors[0][2] / (target_ratio) * 100
        print(f"没有两个电阻值的比值等于 {target_ratio:.2f}，但是电阻值 {resistors[0][0]:.2f} 和 {resistors[0][1]:.2f} 的比值最接近，误差为 {diff_ratio:.4f}%")
    else:
        print(f"在 E24 数系中，以下电阻值组合的比值等于 {target_ratio:.2f}：")
        for r1, r2, _ in resistors:
            print(f"{r1:.2f}, {r2:.2f}")

如果参数是33.55，调用后会输出：

>>> print_resistor_pair(33.55)
没有两个电阻值的比值等于 33.55，但是电阻值 91.00 和 2.70 的比值最接近，误差为 0.4581%

GUI 窗口

再实现一个简单的GUI 吧，方便用：

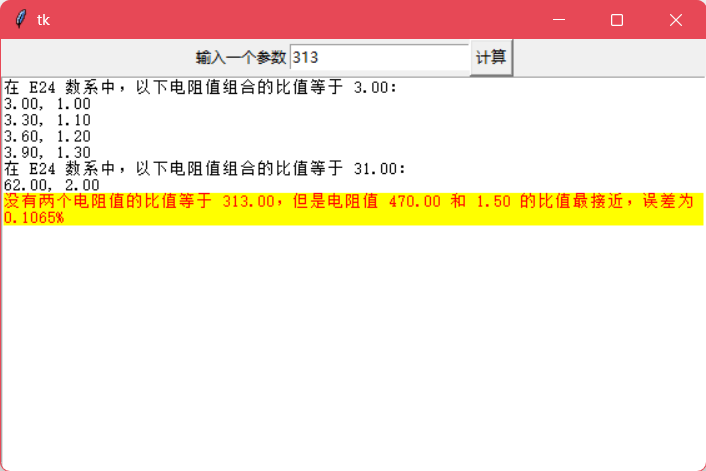
在这里插入图片描述

完整代码如下，保存为.pyw格式的文件，然后双击运行：

import tkinter as tk
import io
import sys

from typing import List, Tuple


def find_e24_resistor_pair(target_ratio: float) -> List[Tuple[float, float, float]]:
    """
    在 E24 优先数系中找到两个电阻值，使它们的比值最接近给定的比值。
    如果有多个解，返回所有较小值不相等且在 1~10 范围内的解。
    如果没有精确匹配的解，返回偏差最小的一组解。
    每个解都是一个三元组 (r1, r2, diff)，其中 r1 和 r2 是电阻值，diff 是偏差。

    :param target_ratio: 目标比值
    :return: 电阻值组合列表
    """
    e24 = [1.0, 1.1, 1.2, 1.3, 1.5, 1.6, 1.8, 2.0, 2.2, 2.4, 2.7,
            3.0, 3.3, 3.6, 3.9, 4.3, 4.7, 5.1, 5.6, 6.2, 6.8,
            7.5, 8.2, 9.1]
    result = []
    min_diff = float('inf')
    epsilon = 1e-9
    min_exponent = math.floor(math.log10(e24[0] * target_ratio))
    max_exponent = min_exponent + 1
    for r2 in e24:
        for r1_base in e24:
            for i in range(min_exponent, max_exponent + 1):
                r1 = r1_base * (10 ** i)
                ratio = r1 / r2
                diff = abs(ratio - target_ratio)
                if diff < epsilon:
                    result.append((r1,r2,diff))
                elif diff < min_diff:
                    min_diff = diff
                    min_result = (r1,r2,diff)
    if len(result) == 0:
        result.append(min_result)

    return result


def print_resistor_pair(target_ratio: float):
    resistors = find_e24_resistor_pair(target_ratio)
    if len(resistors) == 1 and resistors[0][2] > 1e-9:
        diff_ratio = resistors[0][2] / (target_ratio) * 100
        print(f"没有两个电阻值的比值等于 {target_ratio:.2f}，但是电阻值 {resistors[0][0]:.2f} 和 {resistors[0][1]:.2f} 的比值最接近，误差为 {diff_ratio:.4f}%")
    else:
        print(f"在 E24 数系中，以下电阻值组合的比值等于 {target_ratio:.2f}：")
        for r1, r2, _ in resistors:
            print(f"{r1:.2f}, {r2:.2f}")


def on_submit(event=None):
    value_str = entry.get()
    if not value_str:
        return
    text.tag_remove("highlight", "1.0", "end")
    try:
        value = float(value_str)
    except ValueError:
        text.insert(tk.END, "错误：请输入一个有效的浮点数\n")
        text.tag_add("highlight", "end-2l linestart", "end-1l lineend")
        text.yview_moveto(1)
        return
    # 重定向标准输出到字符串缓冲区
    sys.stdout = io.StringIO()
    print_resistor_pair(value)
    # 获取缓冲区中的文本并显示在文本框中
    s = sys.stdout.getvalue()
    text.insert(tk.END, s)
    line_count = s.count('\n')
    text.tag_add("highlight", f"end-{line_count + 1}l linestart", "end-1l lineend")
    text.yview_moveto(1)
    # 恢复标准输出
    sys.stdout = sys.__stdout__

root = tk.Tk()
frame = tk.Frame(root)
frame.pack()
label = tk.Label(frame, text="输入一个参数")
label.pack(side=tk.LEFT)
entry = tk.Entry(frame)
entry.pack(side=tk.LEFT)
entry.bind("<Return>", on_submit)
entry.focus_set()
submit = tk.Button(frame, text="计算", command=on_submit)
submit.pack(side=tk.LEFT)
text = tk.Text(root)
text.pack()
text.tag_config("highlight", background="yellow", foreground="red")
text.tag_config("gray", foreground="gray")
root.mainloop()