目录
一.数组中重复的数字 [集合]
1.题目要求
2.题目思路
3.题目实现
二.二维数组中的查找 [数组]
1.题目要求
2.题目思路
3.题目实现
三.替换空格 [字符串]
1.题目要求
2.题目思路
3.题目实现
四.从尾到头打印链表 [链表]
1.题目要求
2.题目思路
3.题目实现
五.重建二叉树 [二叉树]
1.题目要求
2.题目思路
3.题目实现
六.二叉树的下一个结点 [二叉树]
1.题目要求
2.题目思路
3.题目实现
七.用两个栈实现队列 [栈、队列]
1.题目要求
2.题目思路
3.题目实现
八.斐波那契数列 [指针]
1.题目要求
2.题目思路
3.题目实现
九.旋转数组的最小数字 [二分法]
1.题目要求
2.题目思路
3.题目实现
十.矩阵中的路径 [DFS]
1.题目要求
2.题目思路
3.题目实现
一.数组中重复的数字 [集合]
1.题目要求

给定数组,判断数组中重复的数字,并任意返回重复数字,如果没有则返回 -1。
2.题目思路
如果元素不在 set 中:添加元素
如果元素在 set 中:找到重复元素,返回 -1
如果没有重复元素:返回 -1
Tips:
借助 set 实现 o(n) 的存储空间,遍历 list 需要 o(n) 的时间消耗
3.题目实现
class Solution:
def duplicate(self , numbers: List[int]) -> int:
# write code here
# 特殊情况
if (len(numbers) < 1):
return -1
# 常规情况
numSet = set()
for i in numbers:
if i in numSet:
return i
else:
numSet.add(i)
return -1根据上面的思路,首先判断数组为空的情况,随后只需依次添加至 set 判断即可。

二.二维数组中的查找 [数组]
1.题目要求
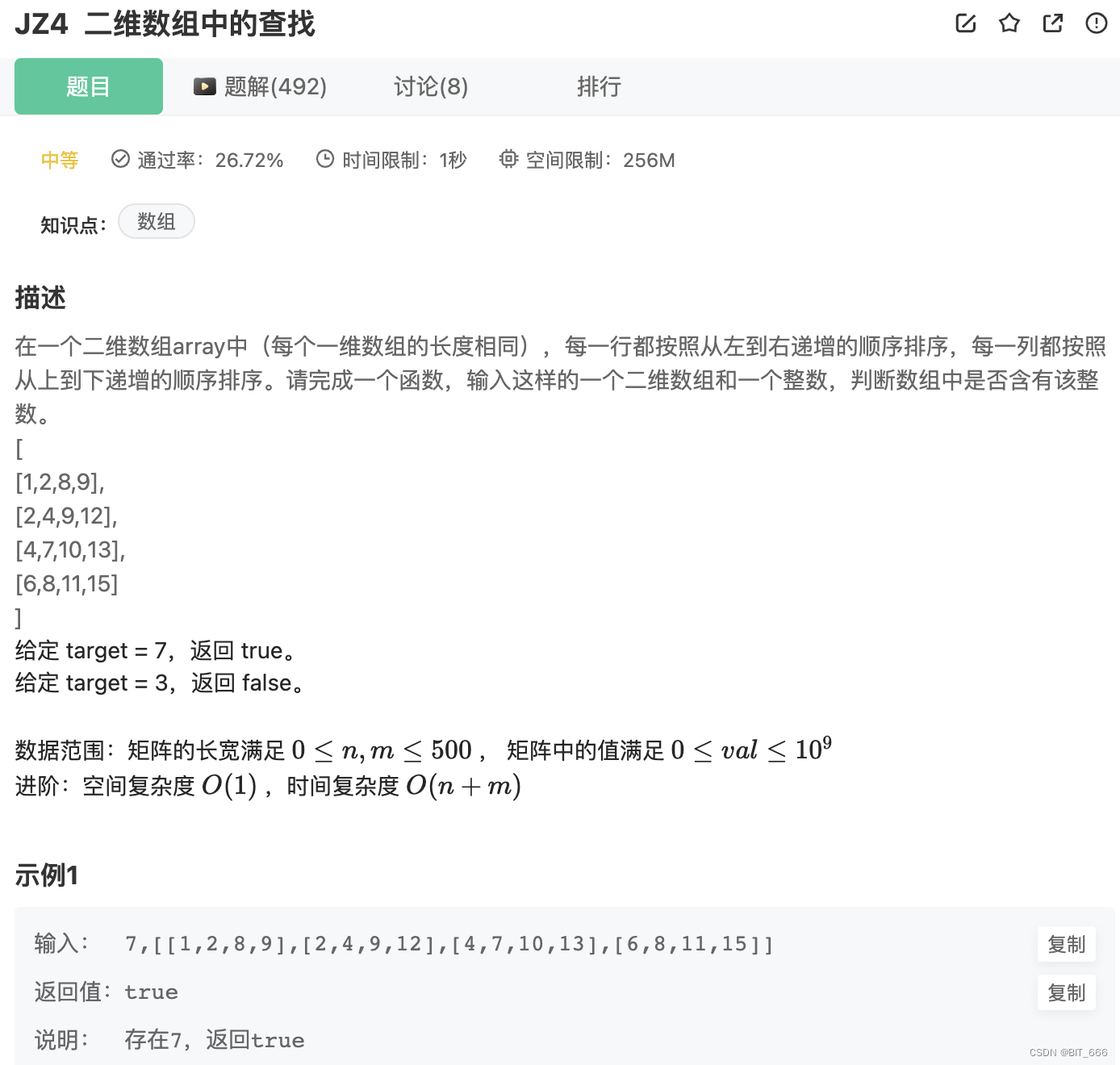
注意这里二维数组按行,按列均是递增的。
2.题目思路
首先遍历 row 行:
如果 target < arr[row][0] 即第一个元素,直接 pass 快进到第二行
如果 target >= arr[row][0],由于数组递增,在数组内执行二分查找
Tips:
遍历数组 row 时间复杂度 O(n),二分查找时间复杂度 O(logn),空间复杂度只需记录 left 和 right。
3.题目实现
class Solution:
def Find(self , target: int, array: List[List[int]]) -> bool:
# write code here
# 空值判断
row = len(array)
if (row == 0):
return False
col = len(array[0])
if (col == 0):
return False
# 区间外值直接返回
min = array[0][0]
max = array[row - 1][col -1]
if (target < min or target > max):
return False
# 区间内采用二分查找
for i in range(row):
if (target < array[i][0]):
continue
else:
left = 0
right = col - 1
while left <= right:
mid = (left + right) // 2
if (array[i][mid] == target):
return True
elif array[i][mid] > target:
right = mid - 1
else:
left = mid + 1
return False空值判断 - 判断数组 row 或 col 为 0 的情况,如果为 0 直接退出
区间判断 - 由于按行按列递增,如果 target < min 或者 target > max,直接退出
二分查找 - 按照题目思路在规定区间进行二分查找即可

三.替换空格 [字符串]
1.题目要求
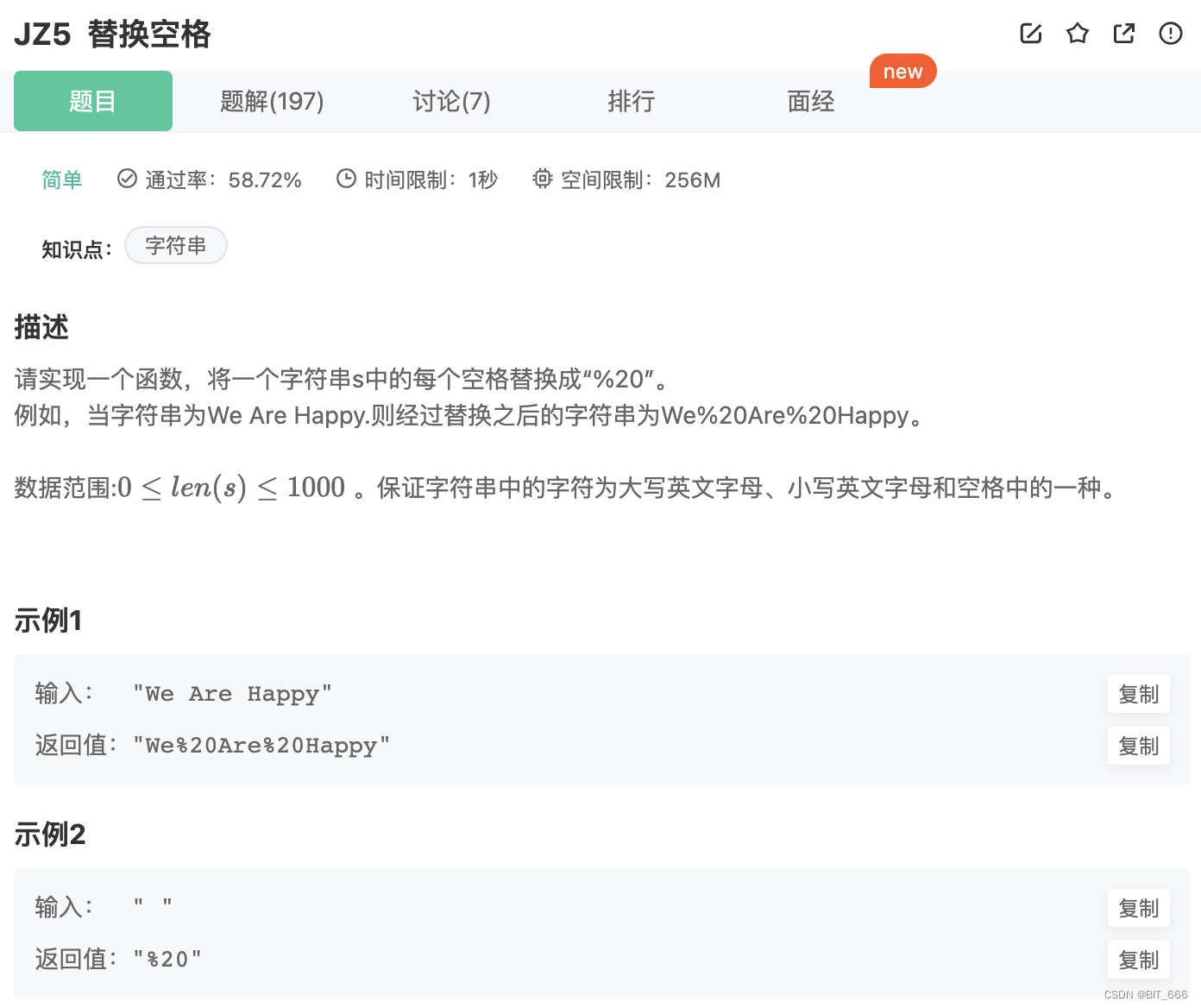
注意这里可能有多个空格
2.题目思路
这题主要考察 python 常规 API 熟悉程度,调用 string.replace 即可实现对应功能。只需注意异常值即可。
3.题目实现
class Solution:
def replaceSpace(self , s: str) -> str:
# write code here
if (s == ""):
return ""
s = s.replace(" ", "%20")
return s
四.从尾到头打印链表 [链表]
1.题目要求
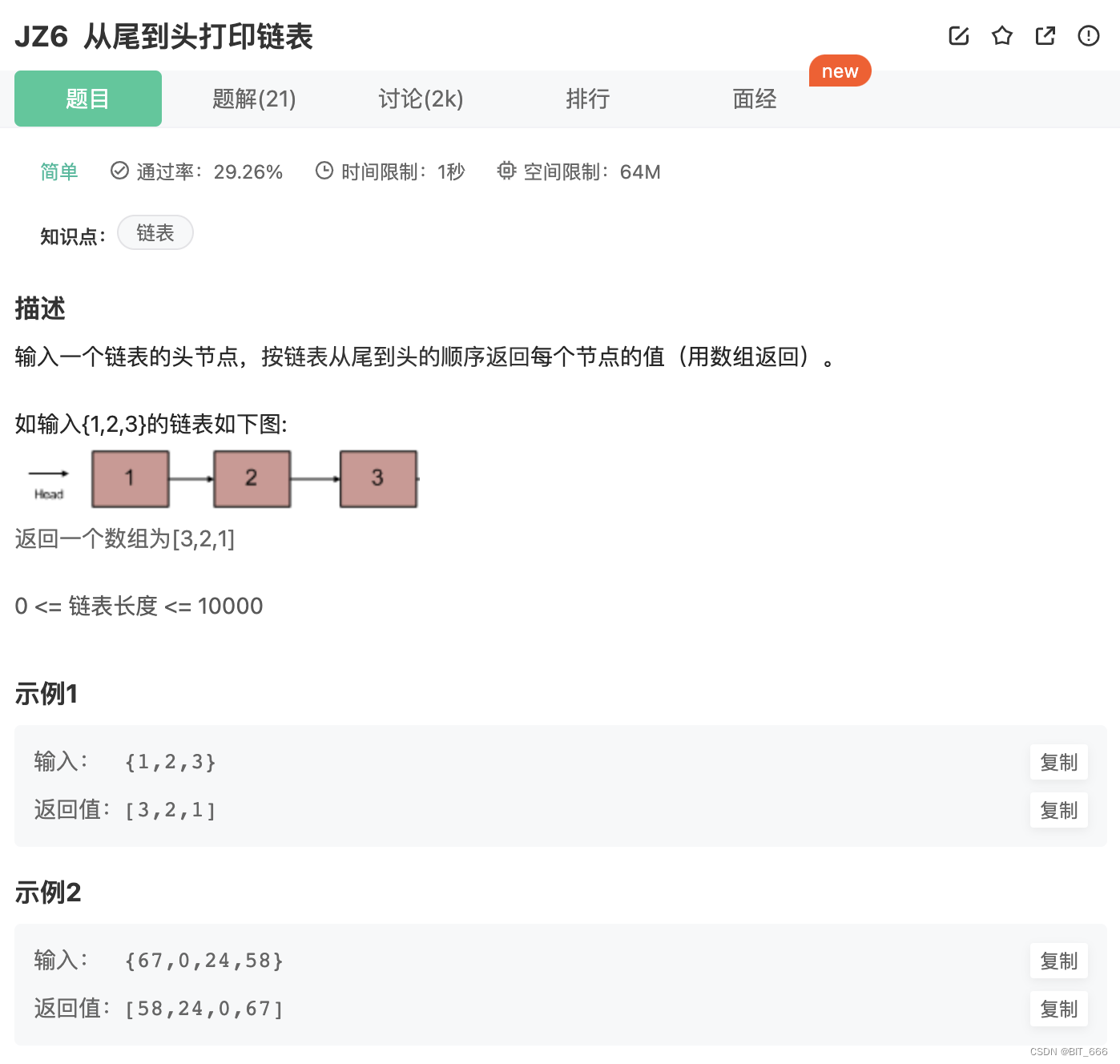
2.题目思路
非常常规的链表题目,只需构建数组依次保存链表结果,随后反转输出列表即可。
3.题目实现
class Solution:
def printListFromTailToHead(self , listNode: ListNode) -> List[int]:
# write code here
res = []
while listNode:
res.append(listNode.val)
listNode = listNode.next
# 数组翻转
return res[::-1]
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
五.重建二叉树 [二叉树]
1.题目要求
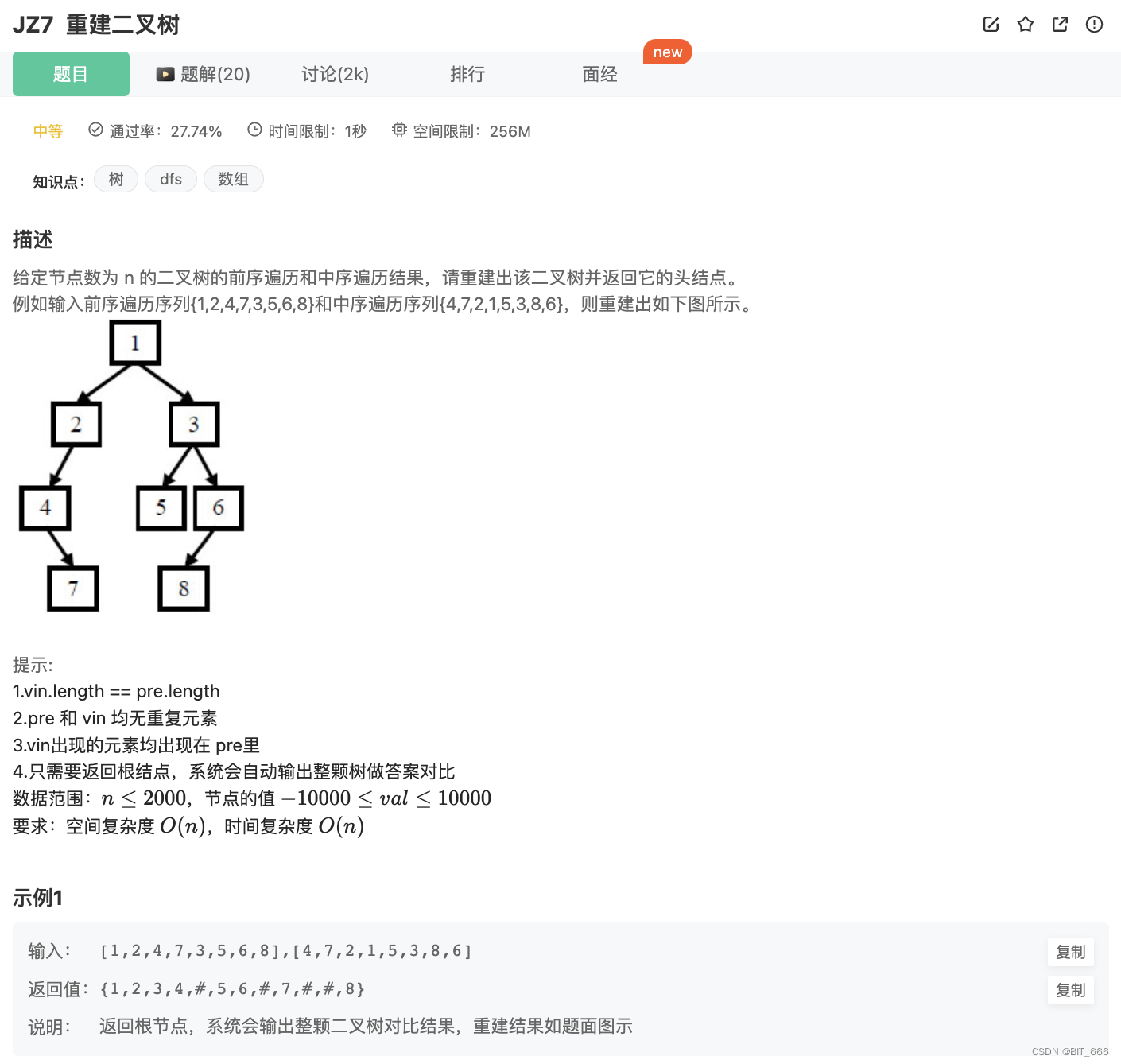
2.题目思路

首先需要清晰二叉树几种遍历的区别:
前序遍历 - 根左右
中序遍历 - 左根右
后续遍历 - 左右根
在结合当前题目,本题给出前序与中序遍历,且元素唯一[很关键]:
A.前序遍历的第一个节点一定是根节点,如图中前序对应首位 1
B.在中序遍历中寻找与根节点相同的点,即为中序遍历中的根节点
C.根据中序遍历的左根右可知,当前节点左边为左子树 472,右边为右子树 5386
D.此时中序遍历得到的两棵子树依然是中序遍历,且前序遍历中对应长度的两个树为其对应的前序遍历 472 为中序遍历,其前序遍历为 247,同理中序遍历 5386,前序遍历 3568
E.所以整体的大树问题转换为两个分开的小树的问题,采用递归的形式解决,我们可以继续分别对 247,472 应用 ABCD 的逻辑,此时通过 247 可知 2 为根节点,左小子树为 47;通过 472 可知根节点 2 无右子树;此时小小树为 47,根节点为4,其没有左节点,所以7为其右节点,5368 同理。
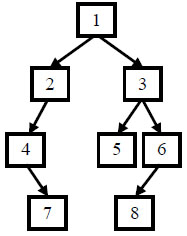
3.题目实现
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
#
# 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
#
#
# @param pre int整型一维数组
# @param vin int整型一维数组
# @return TreeNode类
#
class Solution:
def reConstructBinaryTree(self , pre: List[int], vin: List[int]) -> TreeNode:
# write code here
m = len(pre) # 中序遍历长度 根左右
n = len(vin) # 前序遍历长度 左根右
# 异常情况
if m * n == 0:
return None
# 构建根节点
# 这里前序遍历是根左右,所以 pre 的第一个元素是根节点
root = TreeNode(pre[0])
for i in range(m):
# 找到中序遍历中与根节点相同的点,将二叉树区分
if pre[0] == vin[i]:
# 左子树的前序遍历
leftPre = pre[1:i+1]
# 左子树的中序遍历
leftVin = vin[:i]
root.left = self.reConstructBinaryTree(leftPre, leftVin)
# 右子树的前序遍历
rightPre = pre[i+1:]
# 右子树的中序遍历
rightVin = vin[i+1:]
# 构建右子树
root.right = self.reConstructBinaryTree(rightPre, rightVin)
# 找到与根节点一样的元素就退出了,因为元素唯一
break
return root
六.二叉树的下一个结点 [二叉树]
1.题目要求

这个题其实就是给定层序遍历的情况下,并给定一个节点值,判断中序遍历下该节点值的下一个 Node,与传统 Tree 不同的是,这里还给了一个 next 指针指向 root 父节点。
2.题目思路
常规思路:
最简单的方法就是先找到 root 推导出完整中序遍历,随后依次遍历中序遍历寻找对应值的下一个节点即可。
图形思路:
如果当前节点有右孩子,就找其右子树最左边的孩子节点,给定 2 求后续节点
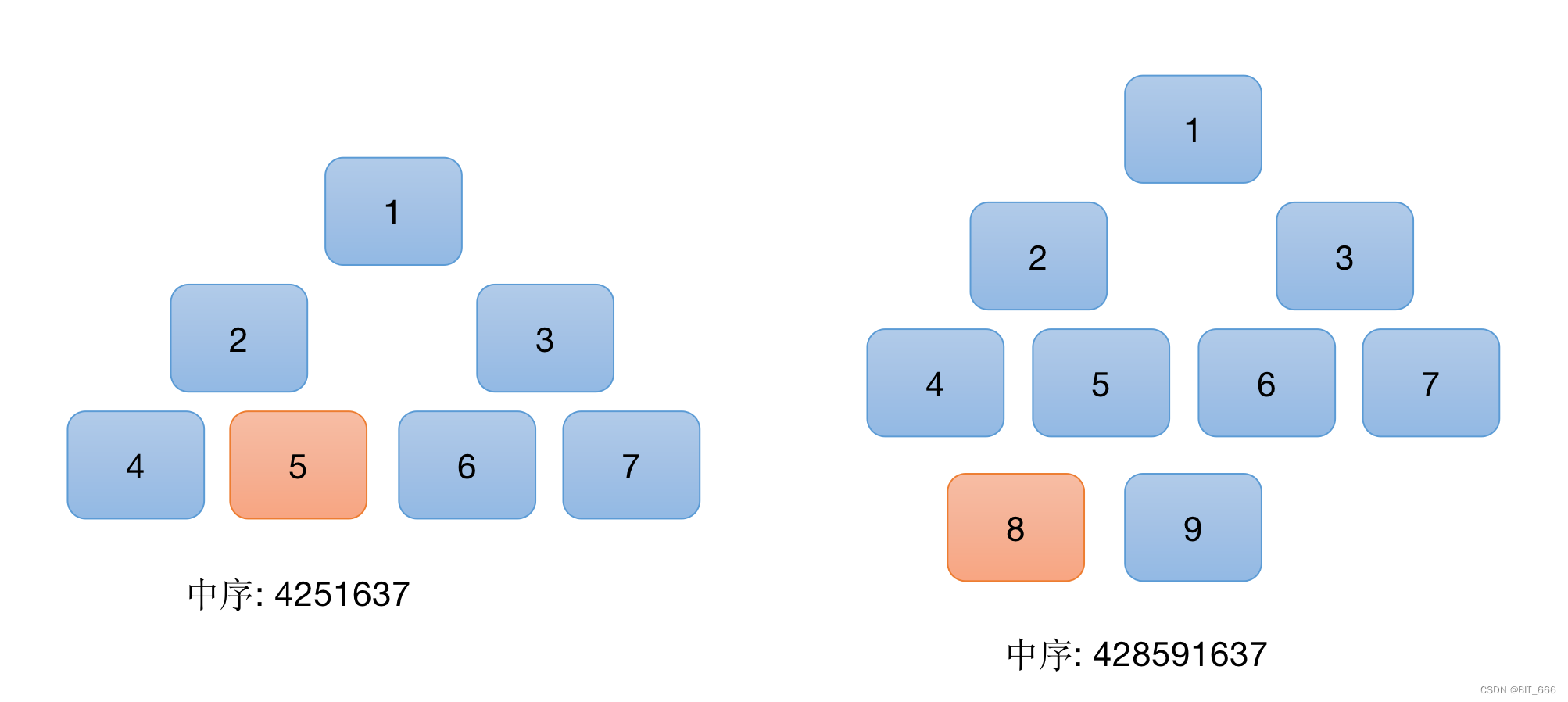
如果当前节点没有右孩子,就向上找其父节点,如果当前节点是其父节点的左孩子,则返回父节点,如果当前节点不是父节点,则一直向上查找直到满足当前节点是父节点的左孩子,并返回,否则返回 None,给定 2 求后续节点
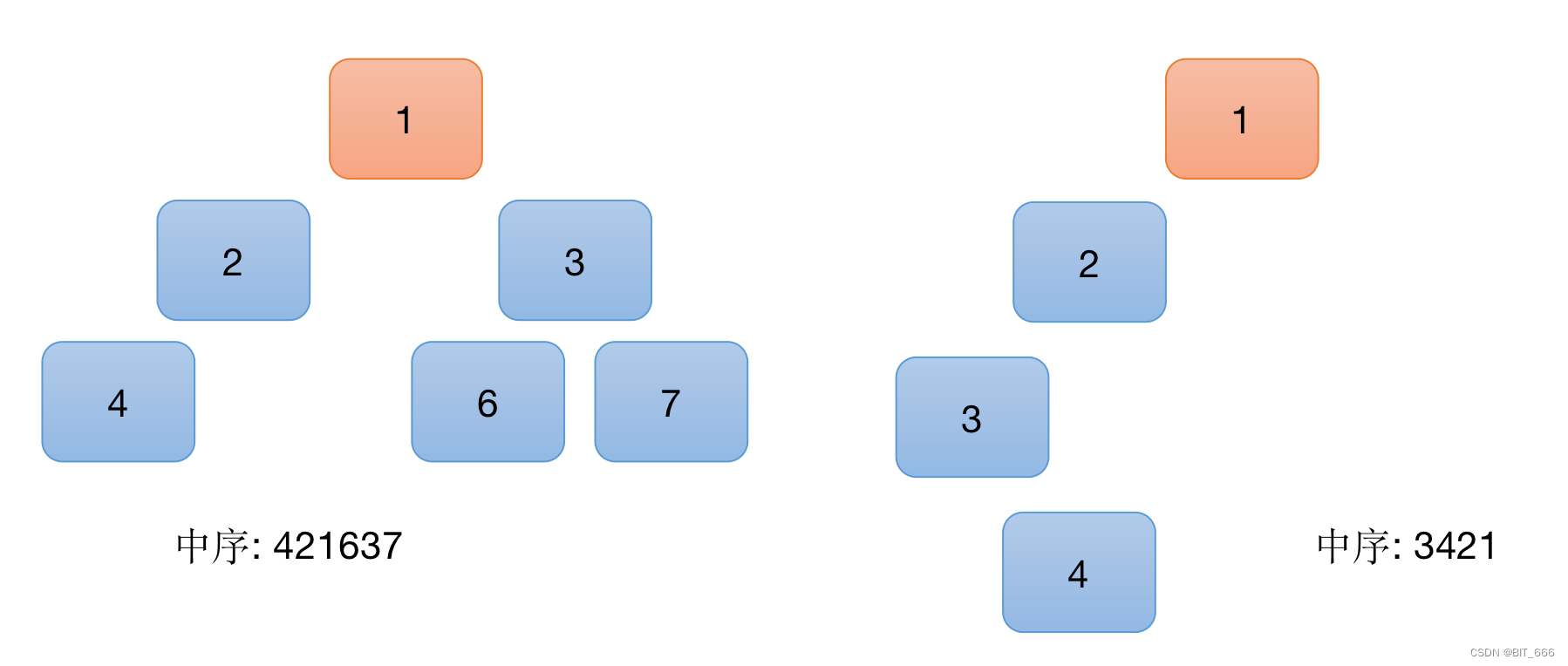
3.题目实现
A.常规思路
# -*- coding:utf-8 -*-
# class TreeLinkNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# self.next = None
class Solution:
nodes = []
def midOrder(self, root):
if root == None:
return
self.midOrder(root.left)
self.nodes.append(root)
self.midOrder(root.right)
def GetNext(self, pNode):
# write code here
# 查找根节点
root = pNode
while root.next:
root = root.next
# 中序遍历打造 Nodes
self.midOrder(root)
# 匹配节点
for i in range(len(self.nodes) - 1):
cur = self.nodes[i]
if pNode == cur:
return self.nodes[i + 1]
return NoneB.图形思路
# -*- coding:utf-8 -*-
# class TreeLinkNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# self.next = None
class Solution:
def GetNext(self, pNode):
# write code here
if not pNode:
return pNode
# 当前节点有右孩子,那么就去找当前节点右子树最左边的那个孩子节点
if pNode.right:
pNode = pNode.right
while pNode.left:
pNode = pNode.left
return pNode
# 当前节点没有右孩子,那么向上找父节点
while pNode.next:
root = pNode.next
if root.left == pNode:
return root
pNode = pNode.next
return None

七.用两个栈实现队列 [栈、队列]
1.题目要求

2.题目思路
本题主要考察队列和栈的特性:
队列 - 元素不可以进行下标访问,先进先出
栈 - 元素不可以进行下标访问,先进后出
用两个栈 [先进后出] 模拟队列 [先进先出] 主要方法就是通过两个栈互相转换,第一个栈先 append 再 pop 给第二个栈,第二个栈再 append,结束后 pop,实现顺序的反转。

3.题目实现
# -*- coding:utf-8 -*-
class Solution:
def __init__(self):
self.stack1 = []
self.stack2 = []
def push(self, node):
self.stack1.append(node)
def pop(self):
# 将第一个栈中内容弹出放入第二个栈中
while self.stack1:
self.stack2.append(self.stack1.pop())
# 第二个栈栈顶就是最先进来的元素,即队首
res = self.stack2.pop()
# 再将第二个栈的元素放回第一个栈
while self.stack2:
self.stack1.append(self.stack2.pop())
return res
八.斐波那契数列 [指针]
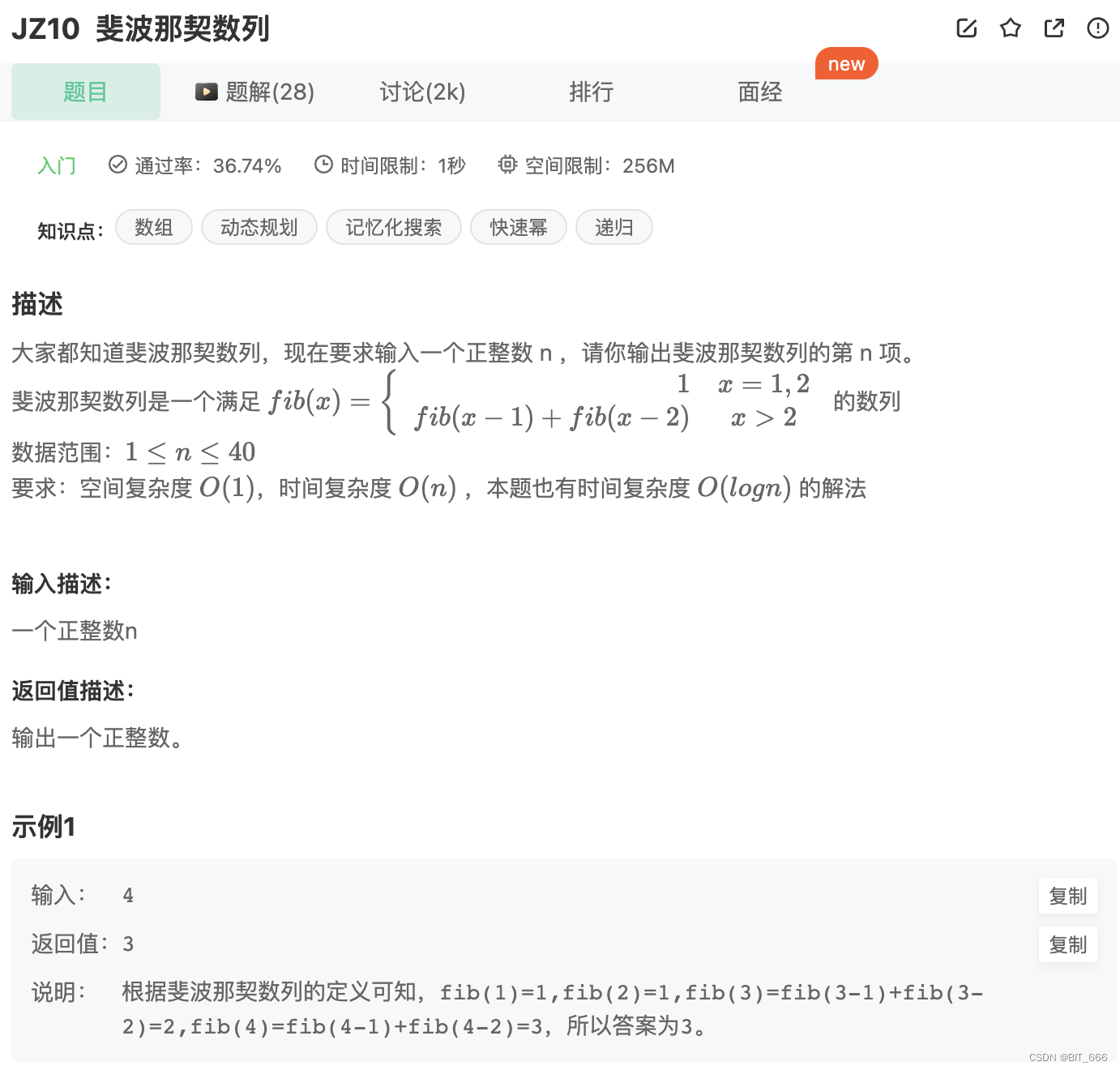
1.题目要求
2.题目思路
利用斐波那契数列的性质,f(n) = f(n-1) + f(n-2),所以我们可以使用三个指针,重复赋值,直到预定结果 n:
n 小于等于 2 - 直接返回 0 或 1
n 大于 2 - 令 re = 0、left = 0、right = 1,依次遍历更新令 re = left + right、left = right、right = re 即可
3.题目实现
#
# @param n int整型
# @return int整型
#
class Solution:
def Fibonacci(self, n: int) -> int:
# 从0开始,第0项是0,第一项是1
if n <= 1:
return n
# 初始化原始值
res = 0
left = 0
right = 1
# 开始循环赋值
for i in range(2, n + 1):
res = left + right
left = right
right = res
return res
九.旋转数组的最小数字 [二分法]
1.题目要求
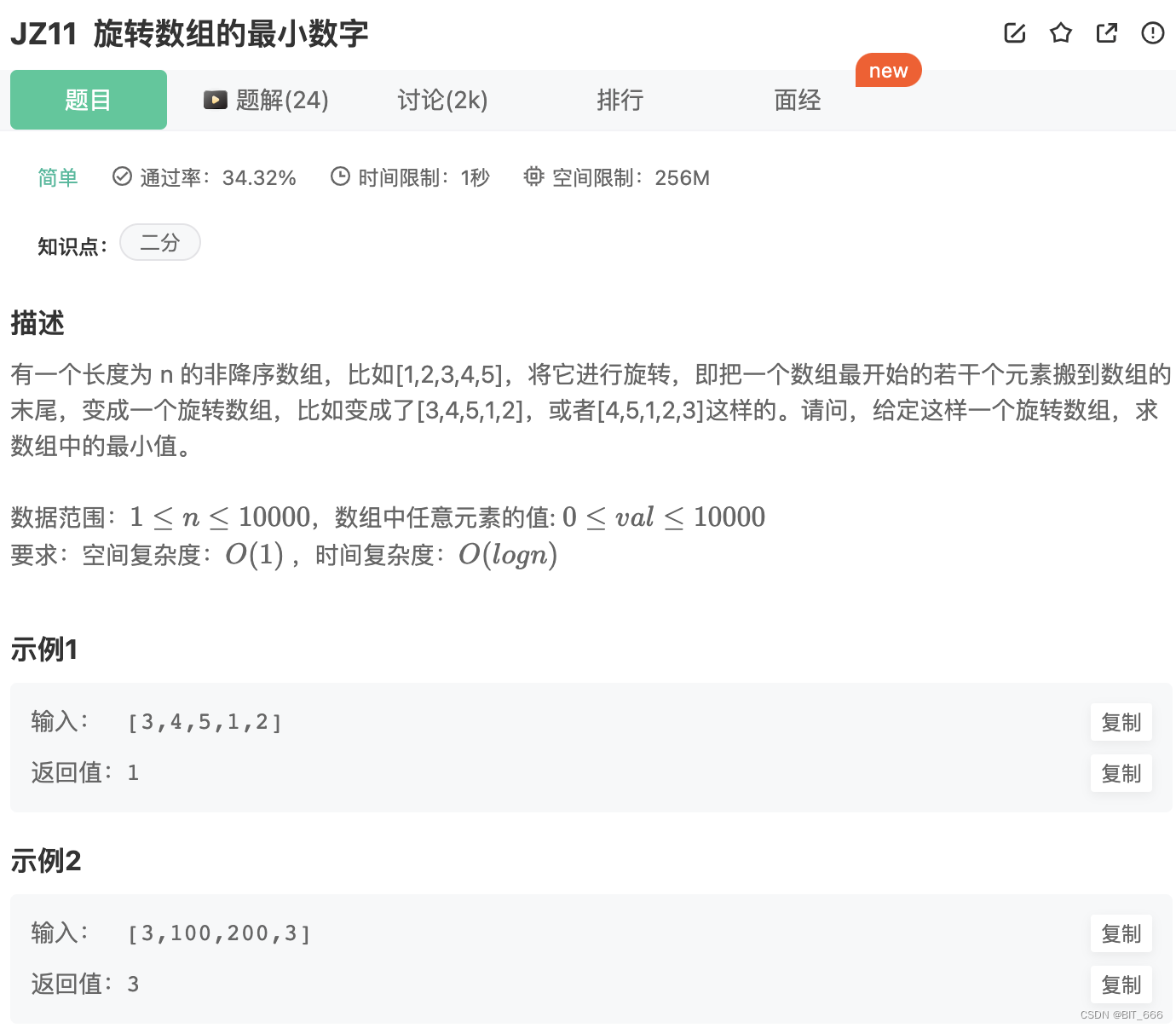
注意数组为非降序,但是可以重复
2.题目思路
虽然数组调换了一次顺序,但是两部分都是非降序的,所以首先根据 mid 和 right 寻找哪一边的数字小,将区间不断缩小寻找最小值即可:

下面是最小值在两边的两种初始情况:

3.题目实现
#
# @param rotateArray int整型一维数组
# @return int整型
#
class Solution:
def minNumberInRotateArray(self , rotateArray: List[int]) -> int:
# 寻找目标区间
left = 0
right = len(rotateArray) - 1
while left < right:
mid = (left + right) // 2
# 最小值在mid右边
if rotateArray[mid] > rotateArray[right]:
left = mid + 1
# 相等,稍作调整继续判断
elif rotateArray[mid] == rotateArray[right]:
right -= 1
# 最小值在mid左边
else:
right = mid
return rotateArray[left]
十.矩阵中的路径 [DFS]
1.题目要求
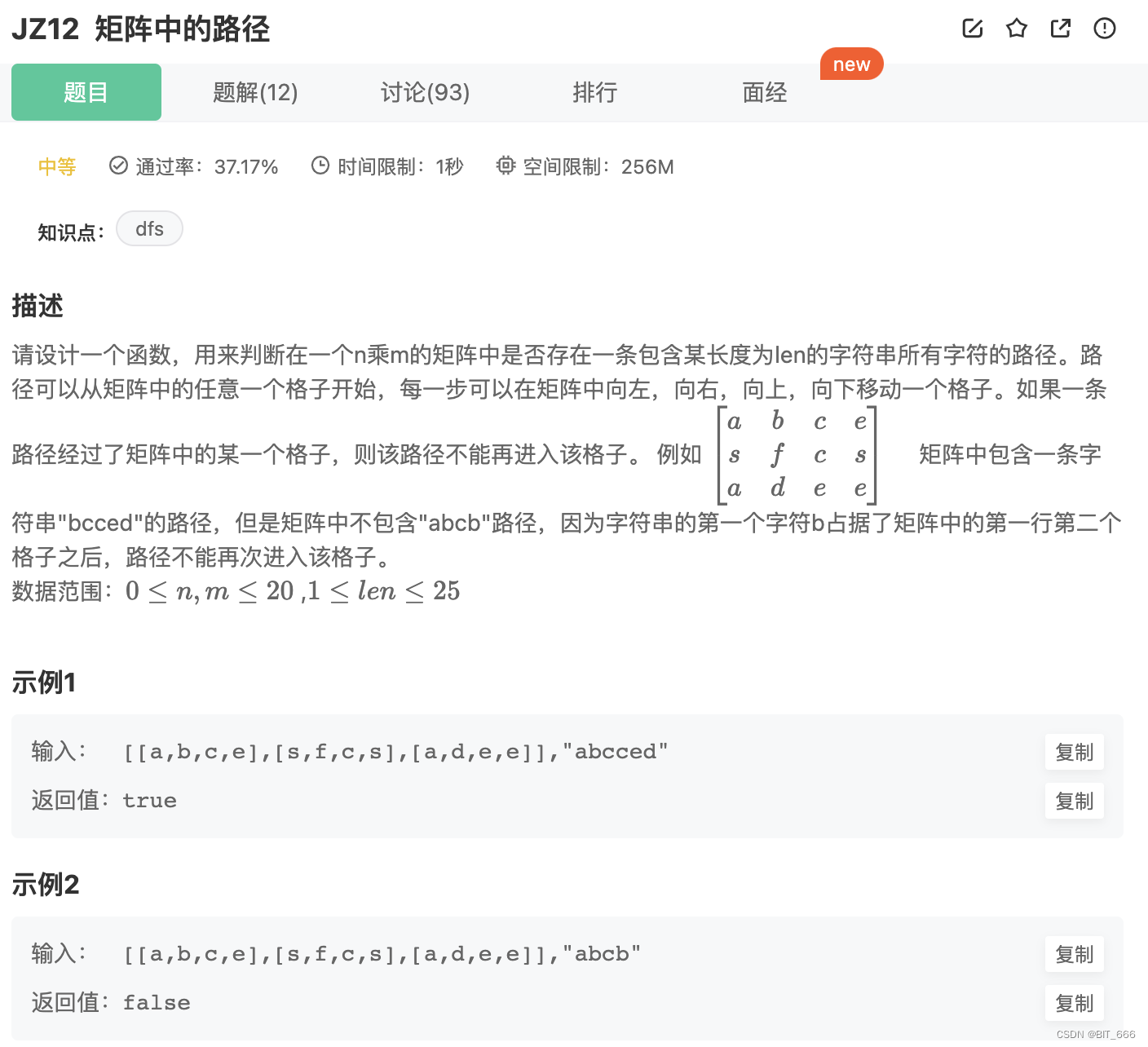
2.题目思路

通过 DFS 每次向四个可能的方向进行探索,同时原题要求不可重复使用,所以需要用到一个同样维度的矩阵记录每个点的使用状态。
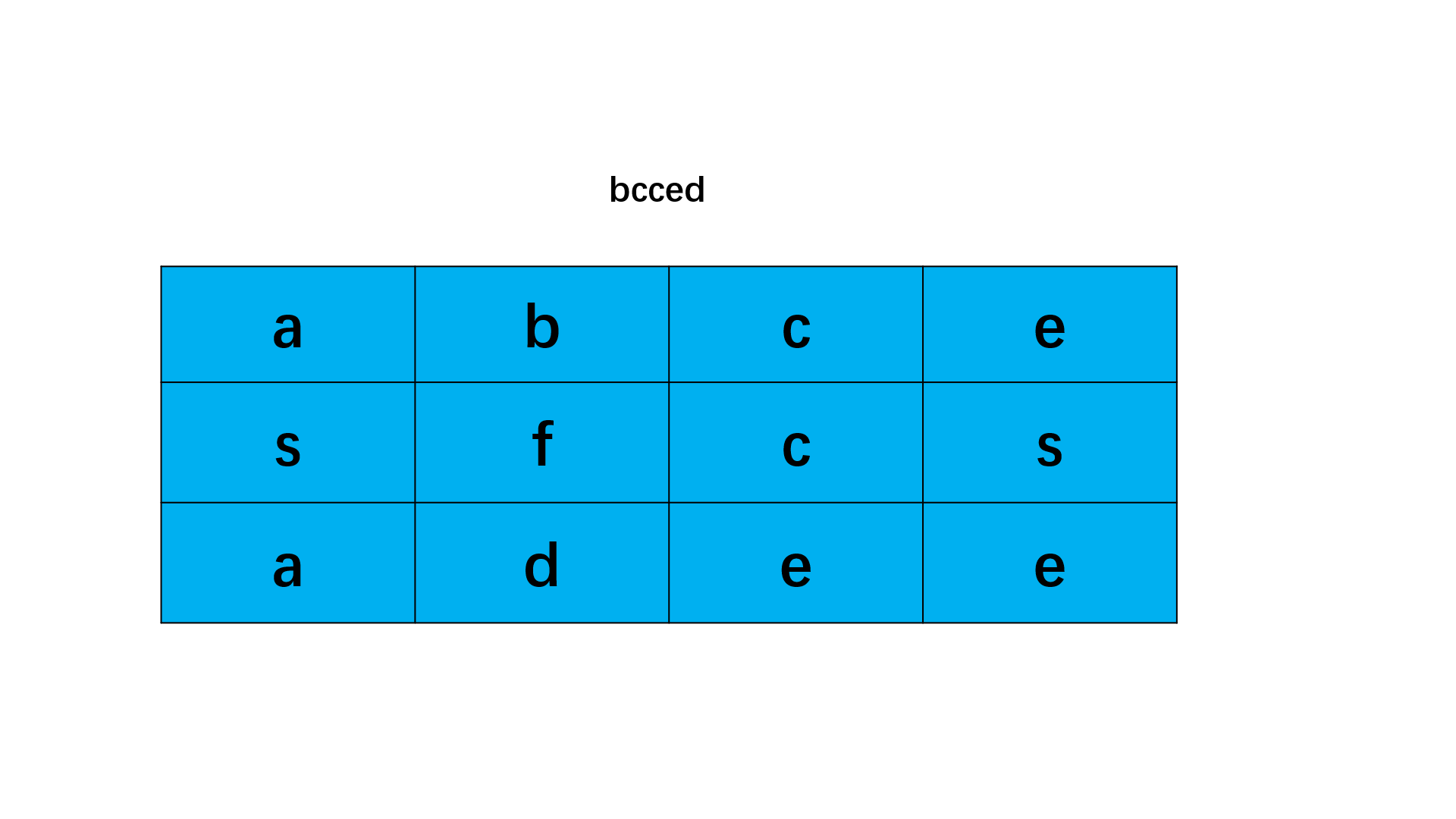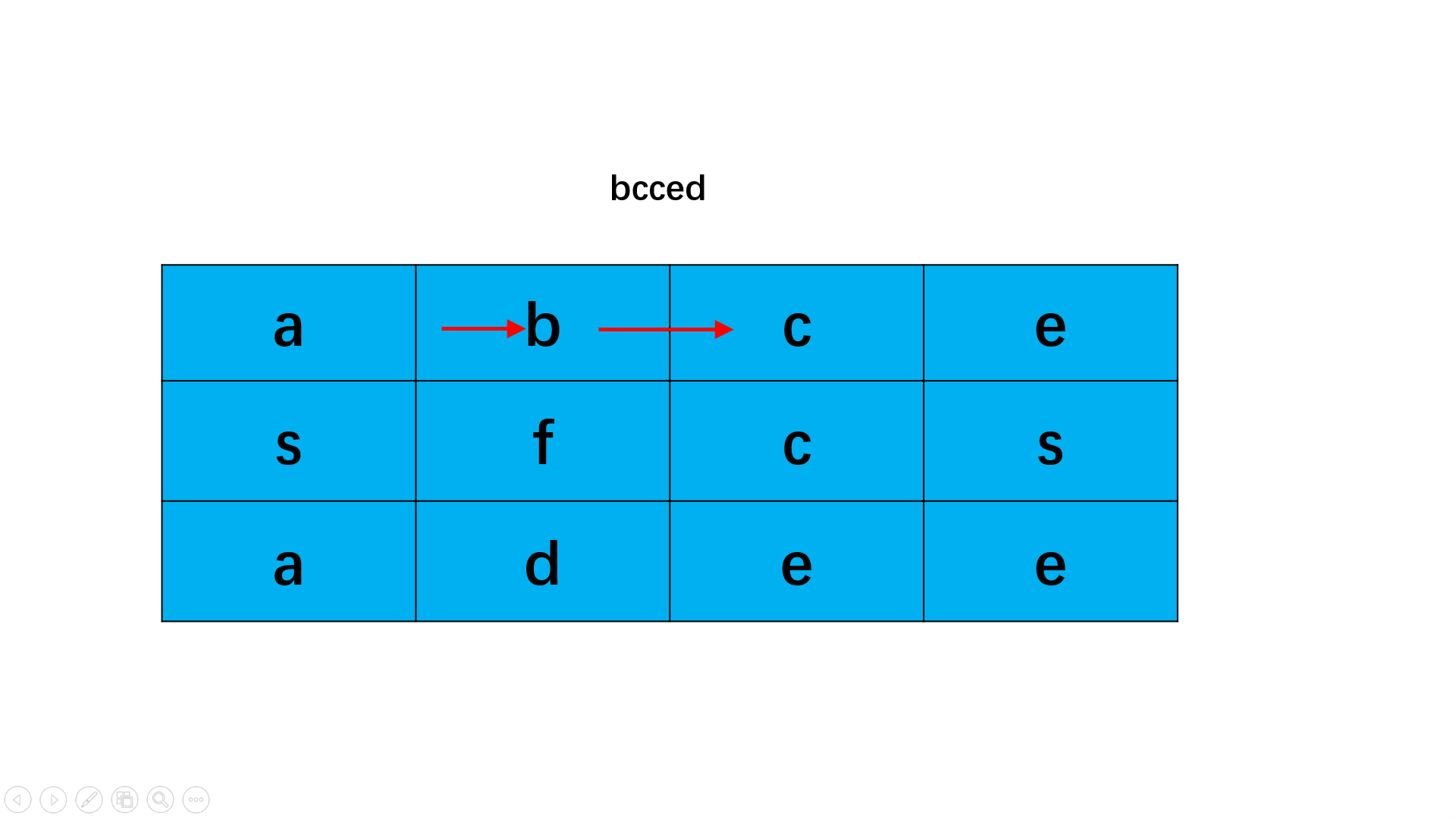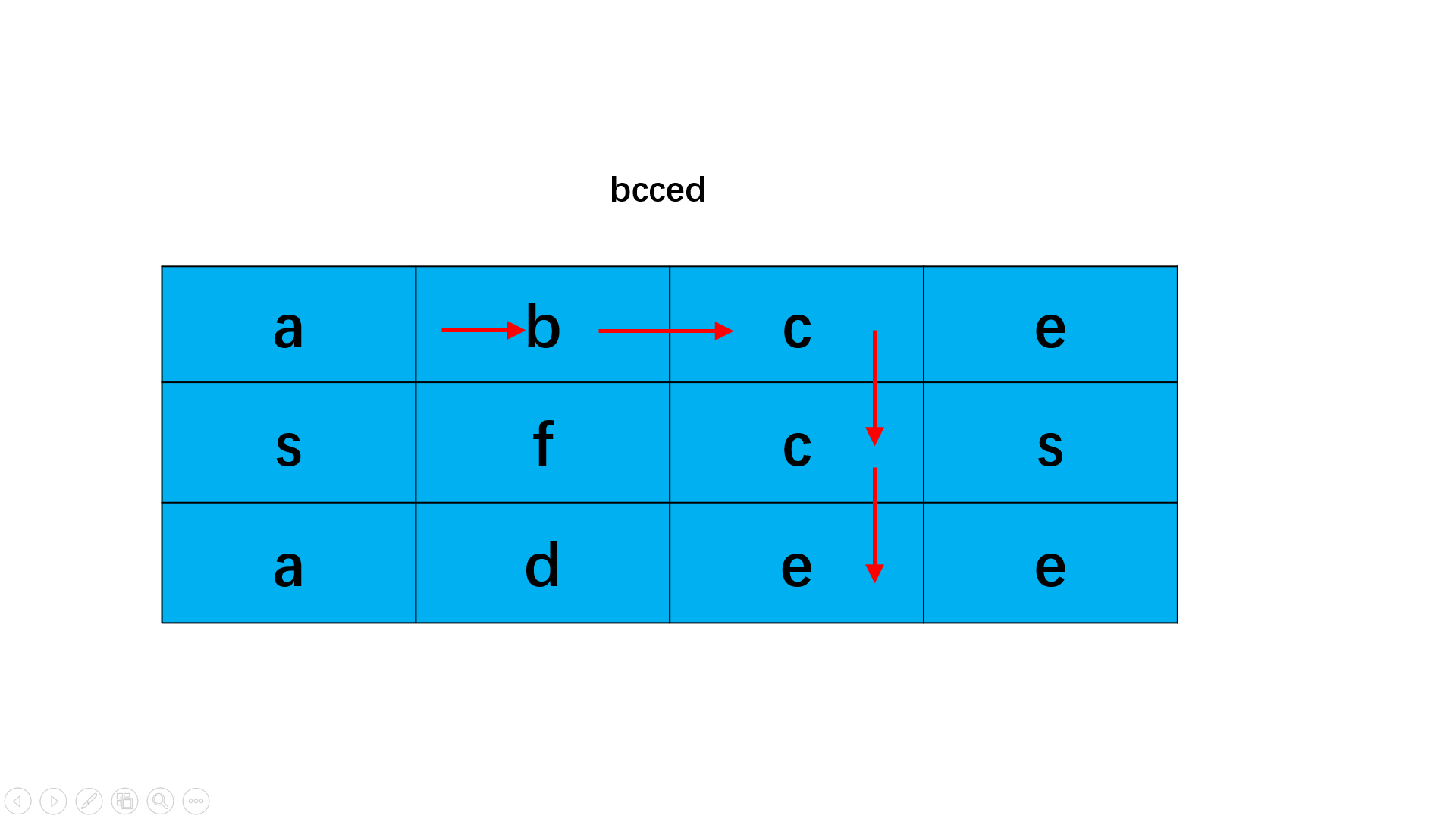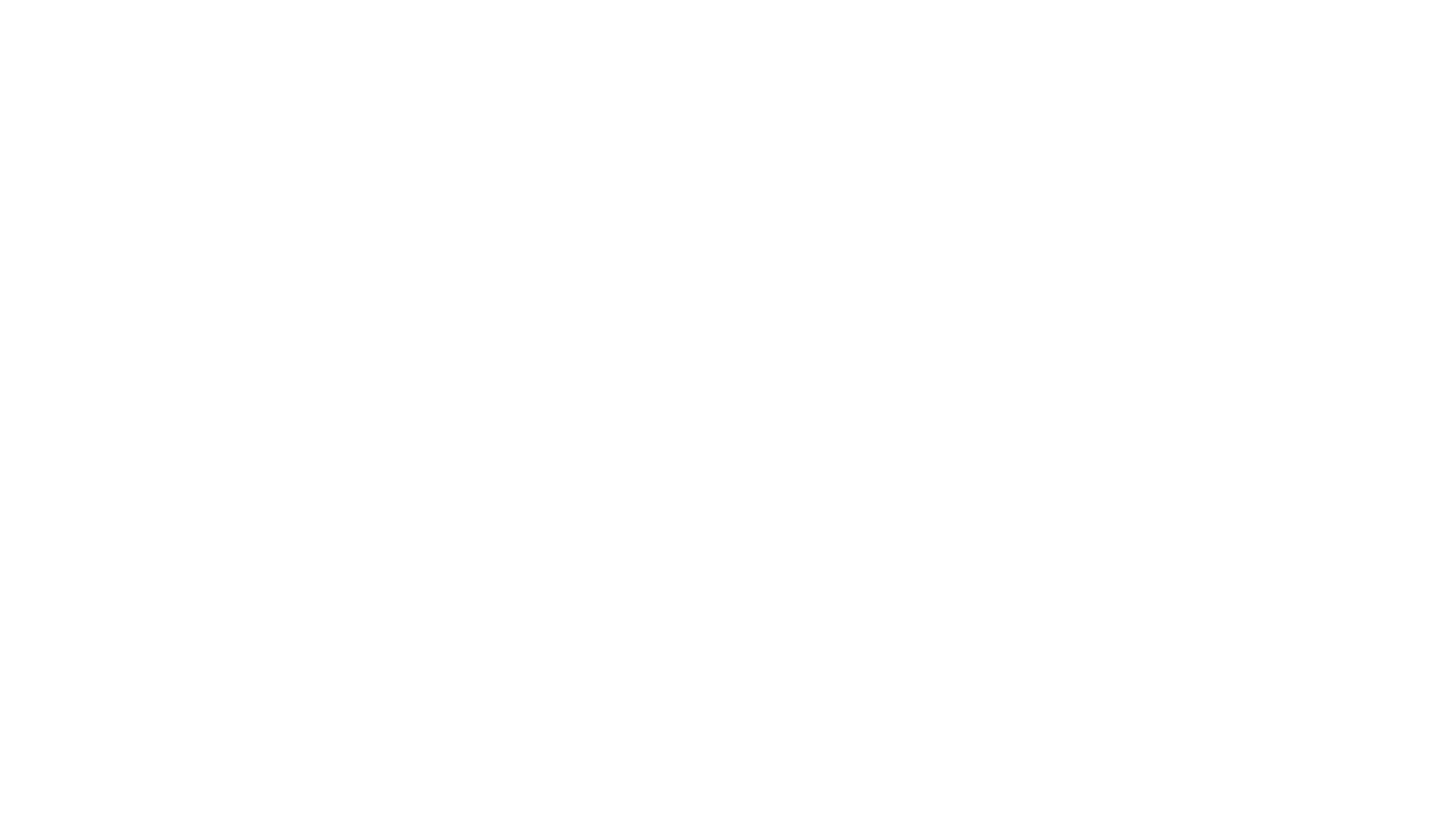
3.题目实现
#
# @param matrix char字符型二维数组
# @param word string字符串
# @return bool布尔型
#
class Solution:
def dfs(self, matrix: List[List[str]], n: int, m: int, i: int, j: int, word: str, k: int, flag: List[List[bool]]) -> bool:
if i < 0 or i >= n or j < 0 or j >= m or (matrix[i][j] != word[k] or flag[i][j]):
# i,j 下标越界、字符串不匹配、字符已使用
return False
# 找到最后一个字符
if k == len(word) - 1:
return True
# 没达到长度继续 DFS
flag[i][j] = True
# 该节点任意方向
if (self.dfs(matrix, n, m, i-1, j, word, k+1, flag) or
self.dfs(matrix, n, m, i+1, j, word, k+1, flag) or
self.dfs(matrix, n, m, i, j-1, word, k+1, flag) or
self.dfs(matrix, n, m, i, j+1, word, k+1, flag)):
return True
# 该点4个方向都没找到
flag[i][j] = False
return False
def hasPath(self , matrix: List[List[str]], word: str) -> bool:
# 空矩阵直接返回
if (len(matrix) == 0):
return False
n = len(matrix)
m = len(matrix[0])
flag = [[False for i in range(m)] for j in range(n)]
for i in range(n):
for j in range(m):
if (self.dfs(matrix, n, m, i, j, word, 0, flag)):
return True
return False