题目所属分类

华为校招

原题链接

给你一个整数数组 nums 和一个 正 整数 k 。你可以选择数组的任一 子序列 并且对其全部元素求和。

数组的 第 k 大和 定义为：可以获得的第 k 个 最大 子序列和（子序列和允许出现重复）

返回数组的 第 k 大和 。

子序列是一个可以由其他数组删除某些或不删除元素排生而来的数组，且派生过程不改变剩余元素的顺序。

注意：空子序列的和视作 0 。

代码案例：输入：nums = [2,4,-2], k = 5
输出：2
解释：所有可能获得的子序列和列出如下，按递减顺序排列：

• 6、4、4、2、2、0、0、-2
  数组的第 5 大和是 2 。

题解

B站的题解视频

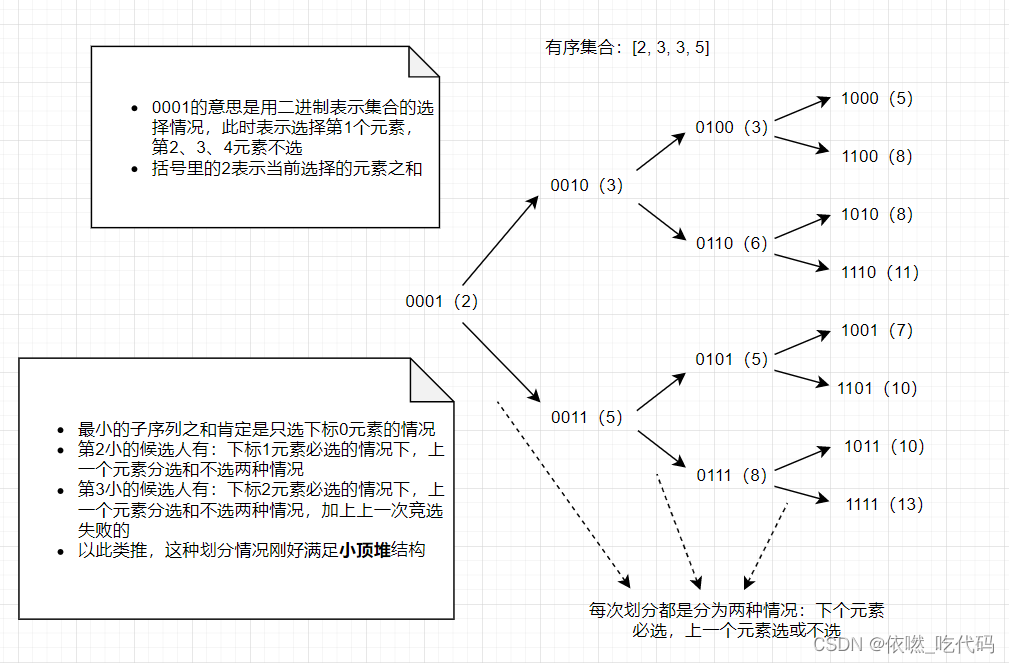
其实也可以用最大堆做， 本质上 就是求出所有正数的和Sum
然后问第K大子序列的和
就是在Sum上减去k-1个最小非空子序列的和
如果是最小堆 那么最终的结果就是 sum - kSum
如果是最大堆 那么直接就是堆顶元素了

具体来说，最大堆维护子序列的和，以及（后续需要减去的）数字的下标 i。

初始时，将 sum 和下标 0 入堆。

最大堆

最小堆
额 自己写的这个最小堆通过不了 最大堆的通过了 不知道哪里有问题 看不出来 有看出的小伙伴可以给我指出错误点

class Solution {
    public long kSum(int[] nums, int k) {
        long Sum = 0l;
        for(int a : nums){
            if(a >= 0) Sum += a ;
            else a = -a ;
        }
        Arrays.sort(nums);
        PriorityQueue<long[]> q = new  PriorityQueue<>((a,b)->(int)(a[0]-b[0]));
        q.offer(new long[]{nums[0],0});
     //k--;
        while(--k > 0){
            long[] t = q.poll();
            int i = (int) t[1];
            if(i + 1 < nums.length){
                q .offer(new long[]{t[0] + nums[i + 1] - nums[i], i + 1});
                // 上一个下标的数要选
                q .offer(new long[]{t[0] + nums[i + 1], i + 1});
 
               // q.offer(new long[]{t[0]+nums[i],i+1});
               // q.offer(new long[]{t[0] + nums[i]-nums[i-1],i+1});//不选
            }
        }
        return Sum-q.peek()[0];
 
    }
}

问题在求和那里 但是我感觉这两种求和方式都一样啊

 
 class Solution {
    public long kSum(int[] nums, int k) {
        long sum = 0l;
        // for(int a : nums){
        //     if(a >= 0) Sum += a ;
        //     else a = -a ;
        // }
        for (var i = 0; i < nums.length; i++)
            if (nums[i] >= 0) sum += nums[i];
            else nums[i] = -nums[i];
        Arrays.sort(nums);
        PriorityQueue<long[]> q = new  PriorityQueue<>((a,b)->(int)(b[0]-a[0]));
        q.offer(new long[]{sum,0});
        while(--k > 0){
            long[] t = q.poll();
            long s = t[0] ;
            int i = (int) t[1];
            if(i  < nums.length){                
               q.offer(new long[]{s-nums[i],i+1});
                if(i > 0) q.offer(new long[]{s - nums[i]+nums[i-1],i+1});//不选
            }
        }
        return q.peek()[0];
         
 
 
    }
}